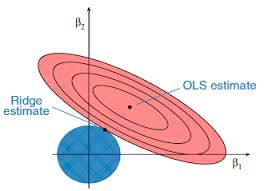
Linear regression is one of the most useful applications in the financial engineer’s tool-kit, but it suffers from a rather restrictive set of assumptions that limit its applicability in areas of research that are characterized by their focus on highly non-linear or correlated variables. The latter problem, referred to as colinearity (or multicolinearity) arises very frequently in financial research, because asset processes are often somewhat (or even highly) correlated. In a colinear system, one can test for the overall significant of the regression relationship, but one is unable to distinguish which of the explanatory variables is individually significant. Furthermore, the estimates of the model parameters, the weights applied to each explanatory variable, tend to be biased.
Over time, many attempts have been made to address this issue, one well-known example being ridge regression. More recent attempts include lasso, elastic net and what I term generalized regression, which appear to offer significant advantages vs traditional regression techniques in situations where the variables are correlated.
In this note, I examine a variety of these techniques and attempt to illustrate and compare their effectiveness.
The Mathematica notebook is also available here.