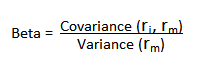What is a Stock Beta?
Around a quarter of a century ago I wrote a paper entitled “Equity Convexity” which – to my disappointment – was rejected as incomprehensible by the finance professor who reviewed it. But perhaps I should not have expected more: novel theories are rarely well received first time around. I remain convinced the idea has merit and may perhaps revisit it in these pages at some point in future. For now, I would like to discuss a related, but simpler concept: beta convexity. As far as I am aware this, too, is new. At least, while I find it unlikely that it has not already been considered, I am not aware of any reference to it in the literature.
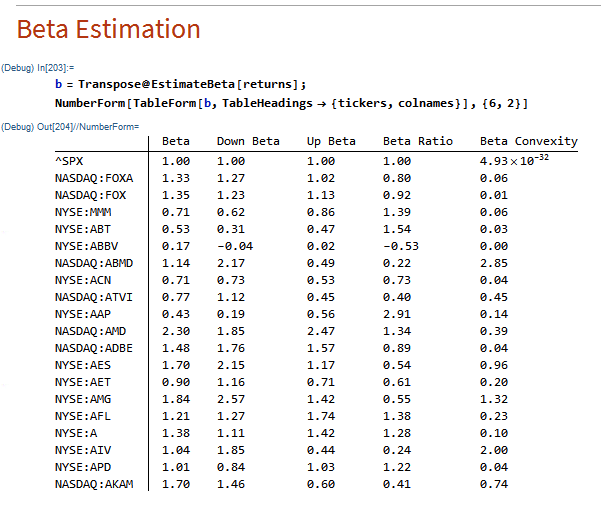
We begin by reviewing the elementary concept of an asset beta, which is the covariance of the return of an asset with the return of the benchmark market index, divided by the variance of the return of the benchmark over a certain period:
Asset betas typically exhibit time dependency and there are numerous methods that can be used to model this feature, including, for instance, the Kalman Filter:
http://jonathankinlay.com/2015/02/statistical-arbitrage-using-kalman-filter/
Beta Convexity
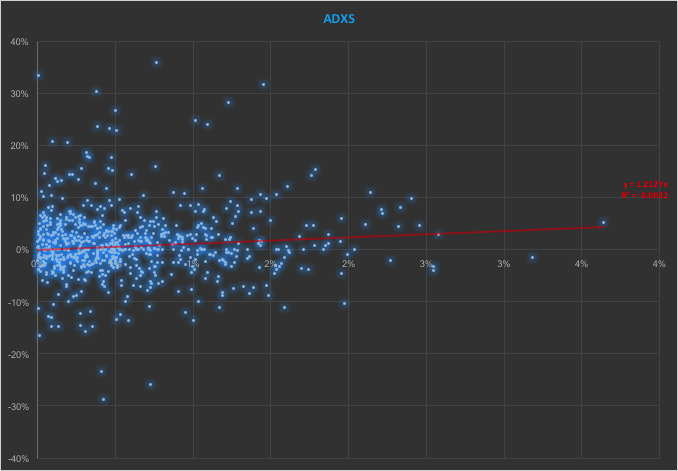
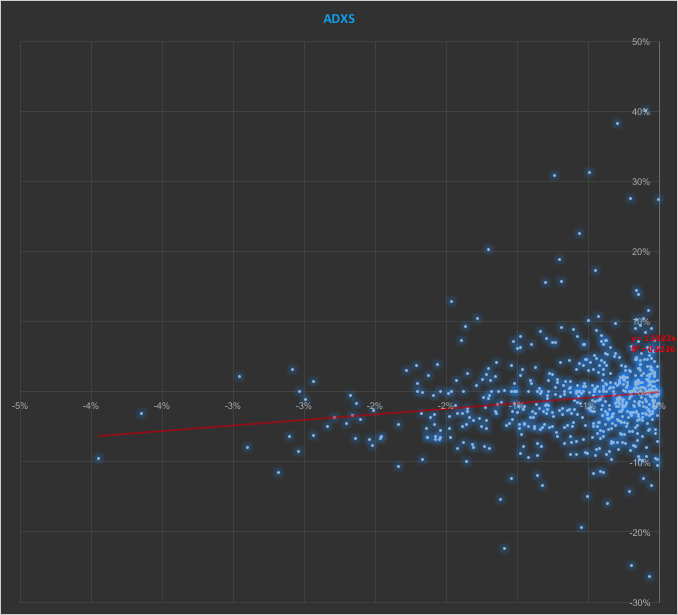
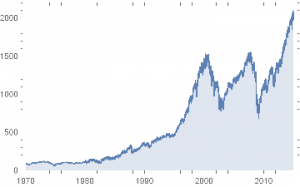
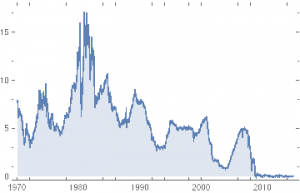
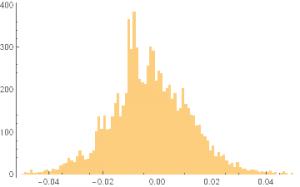
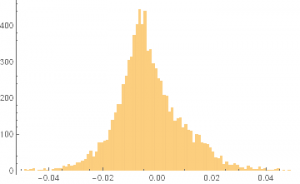
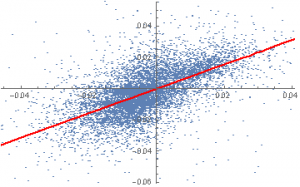
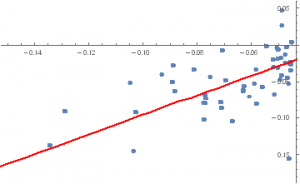
In the context discussed here we set such matters to one side. Instead of considering how an asset beta may vary over time, we look into how it might change depending on the direction of the benchmark index. To take an example, let’s consider the stock Advaxis, Inc. (Nasdaq: ADXS). In the charts below we examine the relationship between the daily stock returns and the returns in the benchmark Russell 3000 Index when the latter are positive and negative.
The charts indicate that the stock beta tends to be higher during down periods in the benchmark index than during periods when the benchmark return is positive. This can happen for two reasons: either the correlation between the asset and the index rises, or the volatility of the asset increases, (or perhaps both) when the overall market declines. In fact, over the period from Jan 2012 to May 2017, the overall stock beta was 1.31, but the up-beta was only 0.44 while the down-beta was 1.53. This is quite a marked difference and regardless of whether the change in beta arises from a change in the correlation or in the stock volatility, it could have a significant impact on the optimal weighting for this stock in an equity portfolio.
Ideally, what we would prefer to see is very little dependence in the relationship between the asset beta and the sign of the underlying benchmark. One way to quantify such dependency is with what I have called Beta Convexity:
Beta Convexity = (Up-Beta – Down-Beta) ^2
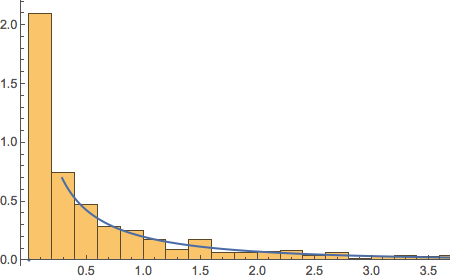
A stock with a stable beta, i.e. one for which the difference between the up-beta and down-beta is negligibly small, will have a beta-convexity of zero. One the other hand, a stock that shows instability in its beta relationship with the benchmark will tend to have relatively large beta convexity.
Index Replication using a Minimum Beta-Convexity Portfolio
One way to apply this concept it to use it as a means of stock selection. Regardless of whether a stock’s overall beta is large or small, ideally we want its dependency to be as close to zero as possible, i.e. with near-zero beta-convexity. This is likely to produce greater stability in the composition of the optimal portfolio and eliminate unnecessary and undesirable excess volatility in portfolio returns by reducing nonlinearities in the relationship between the portfolio and benchmark returns.
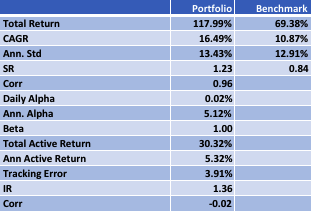
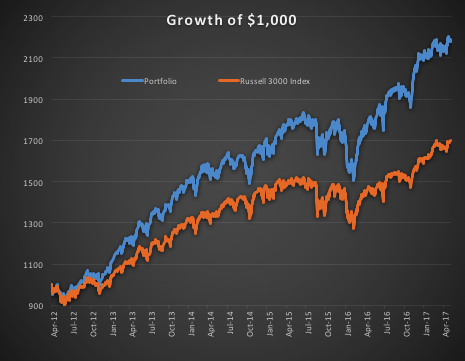
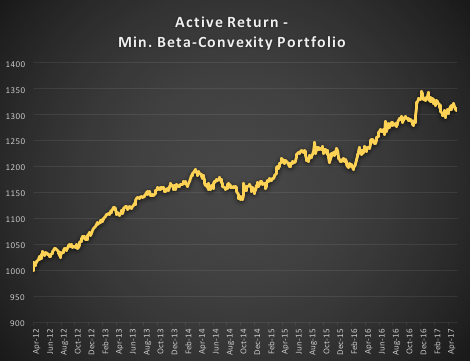
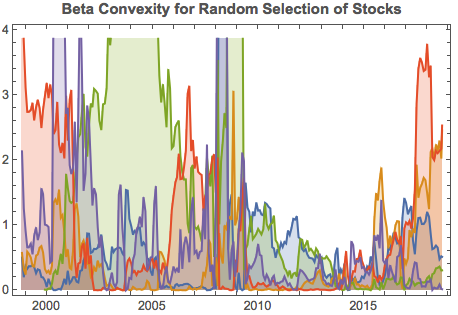
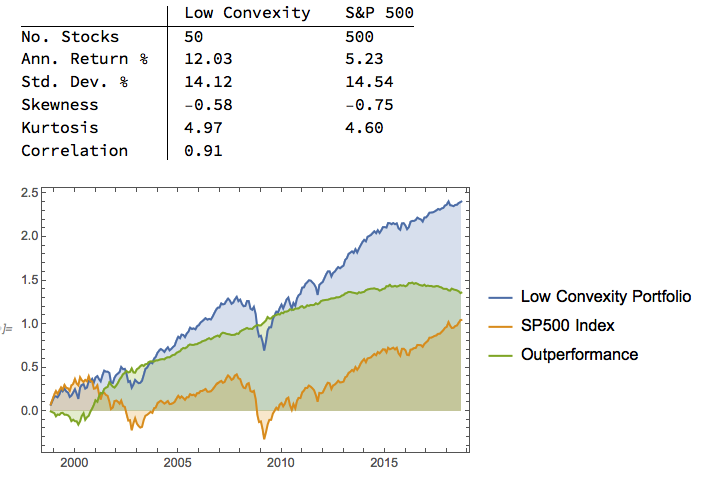
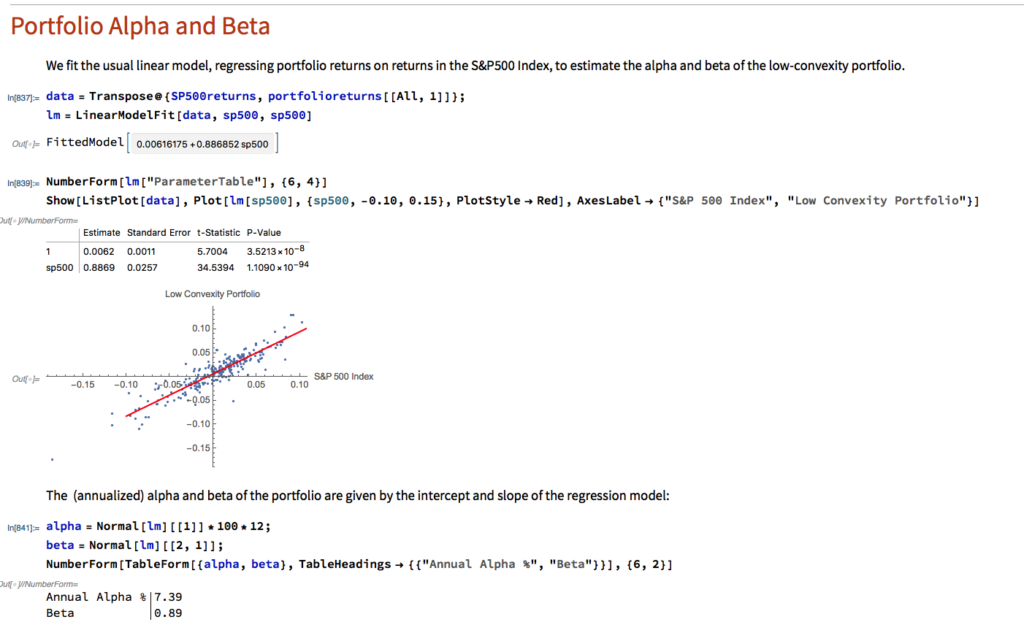
In the following illustration we construct a stock portfolio by choosing the 500 constituents of the benchmark Russell 3000 index that have the lowest beta convexity during the previous 90-day period, rebalancing every quarter (hence all of the results are out-of-sample). The minimum beta-convexity portfolio outperforms the benchmark by a total of 48.6% over the period from Jan 2012-May 2017, with an annual active return of 5.32% and Information Ratio of 1.36. The portfolio tracking error is perhaps rather too large at 3.91%, but perhaps can be further reduced with the inclusion of additional stocks.
Conclusion: Beta Convexity as a New Factor
Beta convexity is a new concept that appears to have a useful role to play in identifying stocks that have stable long term dependency on the benchmark index and constructing index tracking portfolios capable of generating appreciable active returns.
The outperformance of the minimum-convexity portfolio is not the result of a momentum effect, or a systematic bias in the selection of high or low beta stocks. The selection of the 500 lowest beta-convexity stocks in each period is somewhat arbitrary, but illustrates that the approach can scale to a size sufficient to deploy hundreds of millions of dollars of investment capital, or more. A more sensible scheme might be, for example, to select a variable number of stocks based on a predefined tolerance limit on beta-convexity.
Obvious steps from here include experimenting with alternative weighting schemes such as value or beta convexity weighting and further refining the stock selection procedure to reduce the portfolio tracking error.
Further useful applications of the concept are likely to be found in the design of equity long/short and market neural strategies. These I shall leave the reader to explore for now, but I will perhaps return to the topic in a future post.