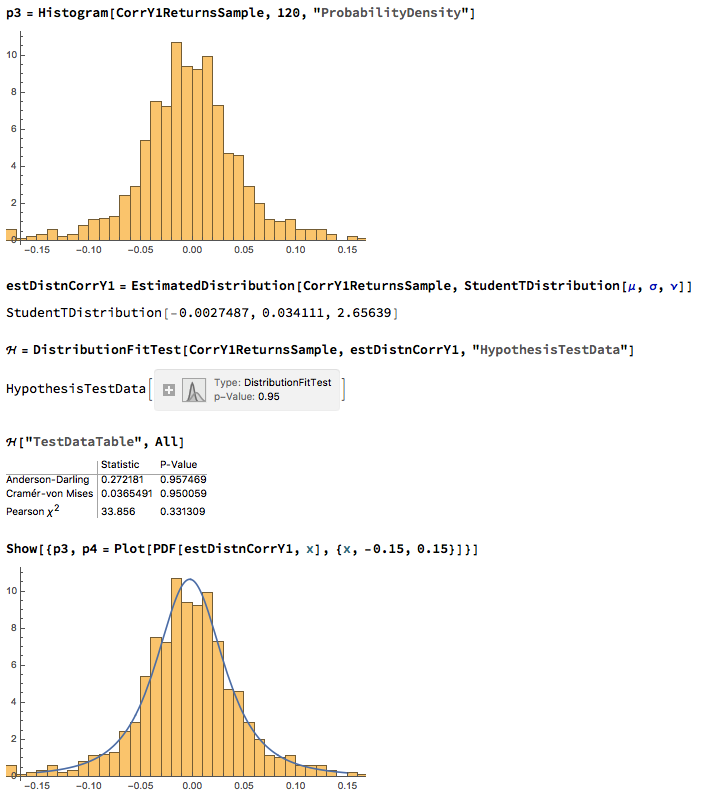
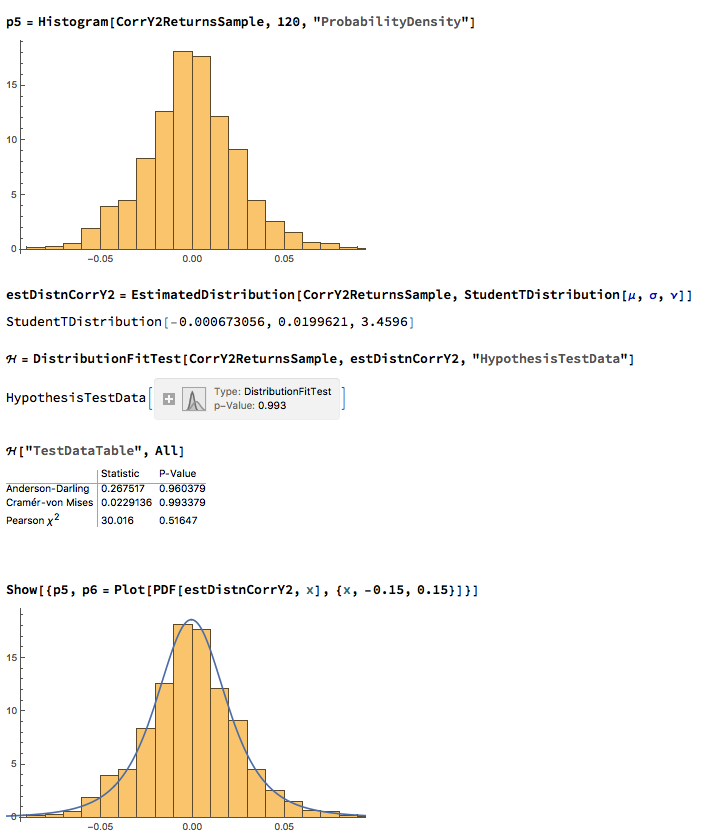
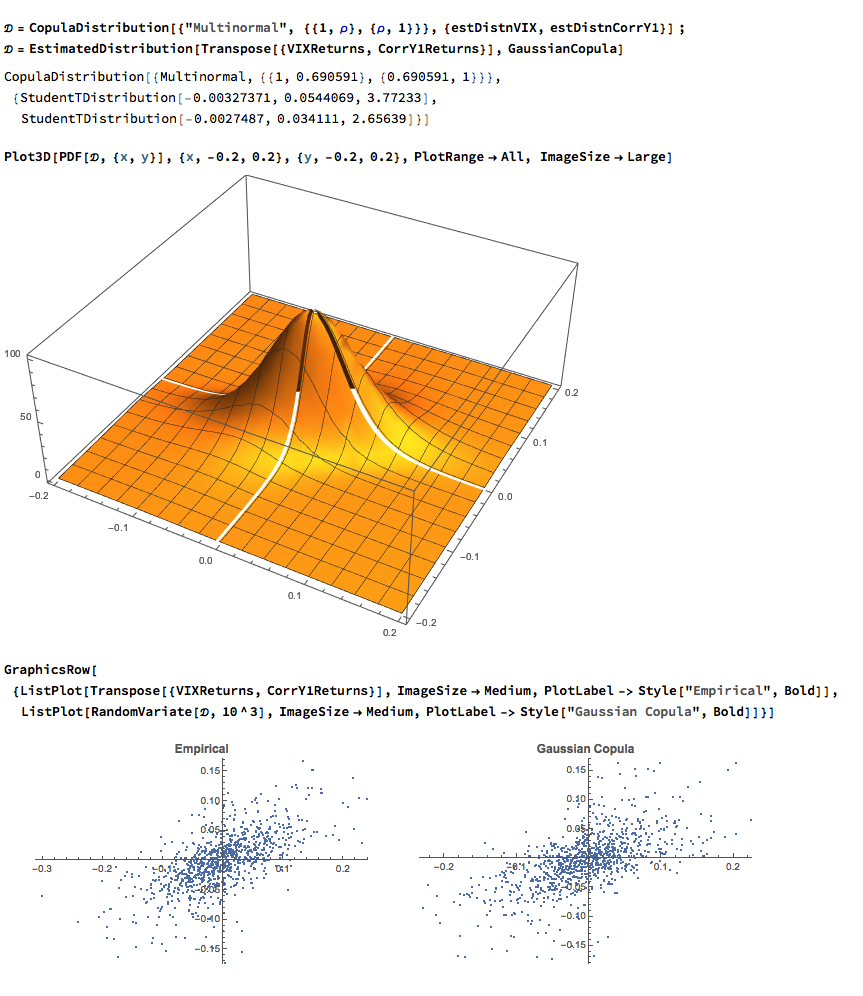
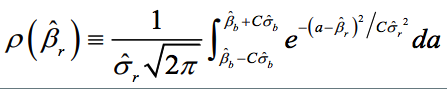Category: Copulas

Posted on

Robustness in Quantitative Research and Trading

What is Strategy Robustness?  What is its relevance to Quantitative Research and Trading?

One of the most highly desired properties of any financial model or investment strategy, by investors and managers alike, is robustness.  I would define robustness as the ability of the strategy to deliver a consistent  results across a wide range of market conditions.  It, of course, by no means the only desirable property – investing in Treasury bills is also a pretty robust strategy, although the returns are unlikely to set an investor’s pulse racing – but it does ensure that the investor, or manager, is unlikely to be on the receiving end of an ugly surprise when market conditions adjust.

Robustness is not the same thing as low volatility, which also tends to be a characteristic highly prized by many investors.  A strategy may operate consistently, with low volatility in certain market conditions, but behave very differently in other.  For instance, a delta-hedged short-volatility book containing exotic derivative positions.   The point is that empirical researchers do not know the true data-generating process for the markets they are modeling. When specifying an empirical model they need to make arbitrary assumptions. An example is the common assumption that assets returns follow a Gaussian distribution.  In fact, the empirical distribution of the great majority of asset process exhibit the characteristic of “fat tails”, which can result from the interplay between multiple market states with random transitions.  See this post for details:

http://jonathankinlay.com/2014/05/a-quantitative-analysis-of-stationarity-and-fat-tails/

 

In statistical arbitrage, for example, quantitative researchers often make use of cointegration models to build pairs trading strategies.  However the testing procedures used in current practice are not sufficient powerful to distinguish between cointegrated processes and those whose evolution just happens to correlate temporarily, resulting in the frequent breakdown in cointegrating relationships.  For instance, see this post:

http://jonathankinlay.com/2017/06/statistical-arbitrage-breaks/

Modeling Assumptions are Often Wrong – and We Know It

We are, of course, not the first to suggest that empirical models are misspecified:

“All models are wrong, but some are useful” (Box 1976, Box and Draper 1987).

 

Martin Feldstein (1982: 829): “In practice all econometric specifications are necessarily false models.”

 

Luke Keele (2008: 1): “Statistical models are always simplifications, and even the most complicated model will be a pale imitation of reality.”

 

Peter Kennedy (2008: 71): “It is now generally acknowledged that econometric models are false and there is no hope, or pretense, that through them truth will be found.”

During the crash of 2008 quantitative Analysts and risk managers found out the hard way that the assumptions underpinning the copula models used to price and hedge credit derivative products were highly sensitive to market conditions.  In other words, they were not robust.  See this post for more on the application of copula theory in risk management:

http://jonathankinlay.com/2017/01/copulas-risk-management/

 

Robustness Testing in Quantitative Research and Trading

We interpret model misspecification as model uncertainty. Robustness tests analyze model uncertainty by comparing a baseline model to plausible alternative model specifications.  Rather than trying to specify models correctly (an impossible task given causal complexity), researchers should test whether the results obtained by their baseline model, which is their best attempt of optimizing the specification of their empirical model, hold when they systematically replace the baseline model specification with plausible alternatives. This is the practice of robustness testing.

SSALGOTRADING AD

Robustness testing analyzes the uncertainty of models and tests whether estimated effects of interest are sensitive to changes in model specifications. The uncertainty about the baseline model’s estimated effect size shrinks if the robustness test model finds the same or similar point estimate with smaller standard errors, though with multiple robustness tests the uncertainty likely increases. The uncertainty about the baseline model’s estimated effect size increases of the robustness test model obtains different point estimates and/or gets larger standard errors. Either way, robustness tests can increase the validity of inferences.

Robustness testing replaces the scientific crowd by a systematic evaluation of model alternatives.

Robustness in Quantitative Research

In the literature, robustness has been defined in different ways:

  • as same sign and significance (Leamer)
  • as weighted average effect (Bayesian and Frequentist Model Averaging)
  • as effect stability We define robustness as effect stability.

Parameter Stability and Properties of Robustness

Robustness is the share of the probability density distribution of the baseline model that falls within the 95-percent confidence interval of the baseline model.  In formulaeic terms:

Formula

  • Robustness is left-–right symmetric: identical positive and negative deviations of the robustness test compared to the baseline model give the same degree of robustness.
  • If the standard error of the robustness test is smaller than the one from the baseline model, ρ converges to 1 as long as the difference in point estimates is negligible.
  • For any given standard error of the robustness test, ρ is always and unambiguously smaller the larger the difference in point estimates.
  • Differences in point estimates have a strong influence on ρ if the standard error of the robustness test is small but a small influence if the standard errors are large.

Robustness Testing in Four Steps

  1. Define the subjectively optimal specification for the data-generating process at hand. Call this model the baseline model.
  2. Identify assumptions made in the specification of the baseline model which are potentially arbitrary and that could be replaced with alternative plausible assumptions.
  3. Develop models that change one of the baseline model’s assumptions at a time. These alternatives are called robustness test models.
  4. Compare the estimated effects of each robustness test model to the baseline model and compute the estimated degree of robustness.

Model Variation Tests

Model variation tests change one or sometimes more model specification assumptions and replace with an alternative assumption, such as:

  • change in set of regressors
  • change in functional form
  • change in operationalization
  • change in sample (adding or subtracting cases)

Example: Functional Form Test

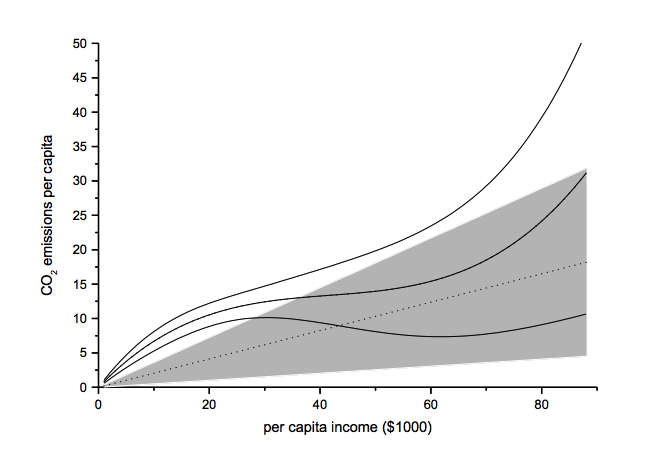
The functional form test examines the baseline model’s functional form assumption against a higher-order polynomial model. The two models should be nested to allow identical functional forms. As an example, we analyze the ‘environmental Kuznets curve’ prediction, which suggests the existence of an inverse u-shaped relation between per capita income and emissions.

Emissions and percapitaincome

Note: grey-shaded area represents confidence interval of baseline model

Another example of functional form testing is given in this review of Yield Curve Models:

http://jonathankinlay.com/2018/08/modeling-the-yield-curve/

Random Permutation Tests

Random permutation tests change specification assumptions repeatedly. Usually, researchers specify a model space and randomly and repeatedly select model from this model space. Examples:

  • sensitivity tests (Leamer 1978)
  • artificial measurement error (Plümper and Neumayer 2009)
  • sample split – attribute aggregation (Traunmüller and Plümper 2017)
  • multiple imputation (King et al. 2001)

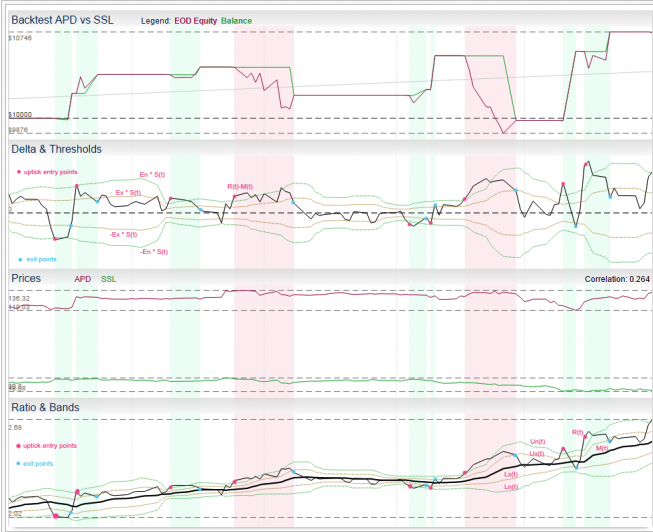
We use Monte Carlo simulation to test the sensitivity of the performance of our Quantitative Equity strategy to changes in the price generation process and also in model parameters:

http://jonathankinlay.com/2017/04/new-longshort-equity/

Structured Permutation Tests

Structured permutation tests change a model assumption within a model space in a systematic way. Changes in the assumption are based on a rule, rather than random.  Possibilities here include:

  • sensitivity tests (Levine and Renelt)
  • jackknife test
  • partial demeaning test

Example: Jackknife Robustness Test

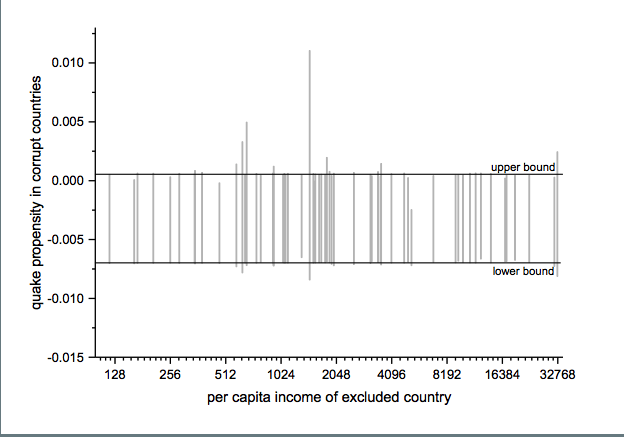
The jackknife robustness test is a structured permutation test that systematically excludes one or more observations from the estimation at a time until all observations have been excluded once. With a ‘group-wise jackknife’ robustness test, researchers systematically drop a set of cases that group together by satisfying a certain criterion – for example, countries within a certain per capita income range or all countries on a certain continent. In the example, we analyse the effect of earthquake propensity on quake mortality for countries with democratic governments, excluding one country at a time. We display the results using per capita income as information on the x-axes.

jackknife

Upper and lower bound mark the confidence interval of the baseline model.

Robustness Limit Tests

Robustness limit tests provide a way of analyzing structured permutation tests. These tests ask how much a model specification has to change to render the effect of interest non-robust. Some examples of robustness limit testing approaches:

  • unobserved omitted variables (Rosenbaum 1991)
  • measurement error
  • under- and overrepresentation
  • omitted variable correlation

For an example of limit testing, see this post on a review of the Lognormal Mixture Model:

http://jonathankinlay.com/2018/08/the-lognormal-mixture-variance-model/

Summary on Robustness Testing

Robustness tests have become an integral part of research methodology. Robustness tests allow to study the influence of arbitrary specification assumptions on estimates. They can identify uncertainties that otherwise slip the attention of empirical researchers. Robustness tests offer the currently most promising answer to model uncertainty.

Posted on

Correlation Copulas

Continuing a previous post, in which we modeled the relationship in the levels of the VIX Index and the Year 1 and Year 2 CBOE Correlation Indices, we next turn our attention to modeling changes in the VIX index.

In case you missed it, the post can be found here:

http://jonathankinlay.com/2017/08/correlation-cointegration/

We saw previously that the levels of the three indices are all highly correlated, and we were able to successfully account for approximately half the variation in the VIX index using either linear regression models or non-linear machine-learning models that incorporated the two correlation indices.  It turns out that the log-returns processes are also highly correlated:

Fig1 Fig2

A Linear Model of VIX Returns

We can create a simple linear regression model that relates log-returns in the VIX index to contemporaneous log-returns in the two correlation indices, as follows.  The derived model accounts for just under 40% of the variation in VIX index returns, with each correlation index contributing approximately one half of the total VIX return.

SSALGOTRADING AD

Fig3

Non-Linear Model of VIX Returns

Although the linear model is highly statistically significant, we see clear evidence of lack of fit in the model residuals, which indicates non-linearities present in the relationship.  So, ext we use a nearest-neighbor algorithm, a machine learning technique that allows us to model non-linear components of the relationship.  The residual plot from the nearest neighbor model clearly shows that it does a better job of capturing these nonlinearities, with lower standard in the model residuals, compared to the linear regression model:

Fig4

Correlation Copulas

Another approach entails the use of copulas to model the inter-dependency between the volatility and correlation indices.  For a fairly detailed exposition on copulas, see the following blog posts:

http://jonathankinlay.com/2017/01/copulas-risk-management/

 

http://jonathankinlay.com/2017/03/pairs-trading-copulas/

We begin by taking a smaller sample comprising around three years of daily returns in the indices.  This minimizes the impact of any long-term nonstationarity in the processes and enables us to fit marginal distributions relatively easily.  First, let’s look at the correlations in our sample data:

Fig5

We next proceed to fit margin distributions to the VIX and Correlation Index processes.  It turns out that the VIX process is well represented by a Logistic distribution, while the two Correlation Index returns processes are better represented by a Student-T density.  In all three cases there is little evidence of lack of fit, wither in the body or tails of the estimated probability density functions:

Fig6 Fig7 Fig8

The final step is to fit a copula to model the joint density between the indices.  To keep it simple I have chosen to carry out the analysis for the combination of the VIX index with only the first of the correlation indices, although in principle there no reason why a copula could not be estimated for all three indices.  The fitted model is a multinormal Gaussian copula with correlation coefficient of 0.69.  of course, other copulas are feasible (Clayton, Gumbel, etc), but Gaussian model appears to provide an adequate fit to the empirical copula, with approximate symmetry in the left and right tails.

Fig9

 

 

 

 

 

Posted on

Pairs Trading with Copulas

Introduction

In a previous post, Copulas in Risk Management, I covered in detail the theory and applications of copulas in the area of risk management, pointing out the potential benefits of the approach and how it could be used to improve estimates of Value-at-Risk by incorporating important empirical features of asset processes, such as asymmetric correlation and heavy tails.

In this post I will take a very different tack, demonstrating how copula models have potential applications in trading strategy design, in particular in pairs trading and statistical arbitrage strategies.

SSALGOTRADING AD

This is not a new concept – in fact the idea occurred to me (and others) many years ago, when copulas began to be widely adopted in financial engineering, risk management and credit derivatives modeling. But it remains relatively under-explored compared to more traditional techniques in this field. Fresh research suggests that it may be a useful adjunct to the more common methods applied in pairs trading, and may even be a more robust methodology altogether, as we shall see.

Recommended Background Reading

http://jonathankinlay.com/2017/01/copulas-risk-management/

http://jonathankinlay.com/2015/02/statistical-arbitrage-using-kalman-filter/

http://jonathankinlay.com/2015/02/developing-statistical-arbitrage-strategies-using-cointegration/

 

Pairs Trading with Copulas

Posted on

Pairs Trading in Practice

Part 1 – Methodologies

It is perhaps a little premature for a deep dive into the Gemini Pairs Trading strategy which trades on our Systematic Algotrading platform.  At this stage all one can say for sure is that the strategy has made a pretty decent start – up around 17% from October 2018.  The strategy does trade multiple times intraday, so the record in terms of completed trades – numbering over 580 – is appreciable (the web site gives a complete list of live trades).  And despite the turmoil through the end of last year the Sharpe Ratio has ranged consistently around 2.5.

One of the theoretical advantages of pairs trading is, of course, that the coupling of long and short positions in a relative value trade is supposed to provide a hedge against market downdrafts, such as we saw in Q4 2018.  In that sense pairs trading is the quintessential hedge fund strategy, embodying the central concept on which the entire edifice of hedge fund strategies is premised.
In practice, however, things often don’t work out as they should. In this thread I want to spend a little time reviewing why that is and to offer some thoughts based on my own experience of working with statistical arbitrage strategies over many years.

Methodology

There is no “secret recipe” for pairs trading:  the standard methodologies are as well known as the strategy concept.  But there are some important practical considerations that I would like to delve into in this post.  Before doing that, let me quickly review the tried and tested approaches used by statistical arbitrageurs.

The Ratio Model is one of the standard pair trading models described in literature. It is based in ratio of instrument prices, moving average and standard deviation. In other words, it is based on Bollinger Bands indicator.

  • we trade pair of stocks A, B, having price series A(t), B(t)
  • we need to calculate ratio time series R(t) = A(t) / B(t)
  • we apply a moving average of type T with period Pm on R(t) to get time series M(t)
  • Next we apply the standard deviation with period Ps on R(t) to get time series S(t)
  • now we can create Z-score series Z(t) as Z(t) = (R(t) – M(t)) / S(t), this time series can give us z-score to signal trading decision directly (in reality we have two Z-scores: Z-scoreask and Z-scorebid as they are calculated using different prices, but for the sake of simplicity let’s now pretend we don’t pay bid-ask spread and we have just one Z-score)

Another common way to visualize  this approach is to think in terms of bands around the moving average M(t):

  • upper entry band Un(t) = M(t) + S(t) * En
  • lower entry band Ln(t) = M(t) – S(t) * En
  • upper exit band Ux(t) = M(t) + S(t) * Ex
  • lower exit band Lx(t) = M(t) – S(t) * Ex

These bands are actually the same bands as in Bollinger Bands indicator and we can use crossing of R(t) and bands as trade signals.

  • We open short pair position, if the Z-score Z(t) >= En (equivalent to R(t) >= Un(t))
  • We open long pair position if the Z-score Z(t) <= -En (equivalent to R(t) <= Ln(t))

In the Regression, Residual or Cointegration approach we construct a linear regression between A(t), B(t) using OLS, where A(t) = β * B(t) + α + R(t)

Because we use a moving window of period P (we calculate new regression each day), we actually get new series β(t), α(t), R(t), where β(t), α(t) are series of regression coefficients and R(t) are residuals (prediction errors)

  • We look at the residuals series  R(t) = A(t) – (β(t) * B(t) + α(t))
  • We next calculate the standard deviation of the residuals R(t), which we designate S(t)
  • Now we can create Z-score series Z(t) as Z(t) = R(t) / S(t) – the time series that is used to generate trade signals, just as in the Ratio model.

The Kalman Filter model provides superior estimates of the current hedge ratio compared to the Regression method.  For a detailed explanation of the techniques, see the following posts (the post on ETF trading contains complete Matlab code).

 

 

Finally,  the rather complex Copula methodology models the joint and margin distributions of the returns process in each stock as described in the following post