Implied Volatility in Merton’s Jump Diffusion Model
The “implied volatility” corresponding to an option price is the value of the volatility parameter for which the Black-Scholes model gives the same price. A well-known phenomenon in market option prices is the “volatility smile”, in which the implied volatility increases for strike values away from the spot price. The jump diffusion model is a generalization of Black\[Dash]Scholes in which the stock price has randomly occurring jumps in addition to the random walk behavior. One of the interesting properties of this model is that it displays the volatility smile effect. In this Demonstration, we explore the Black-Scholes implied volatility of option prices (equal for both put and call options) in the jump diffusion model. The implied volatility is modeled as a function of the ratio of option strike price to spot price.
Option Prices in the Variance Gamma Model
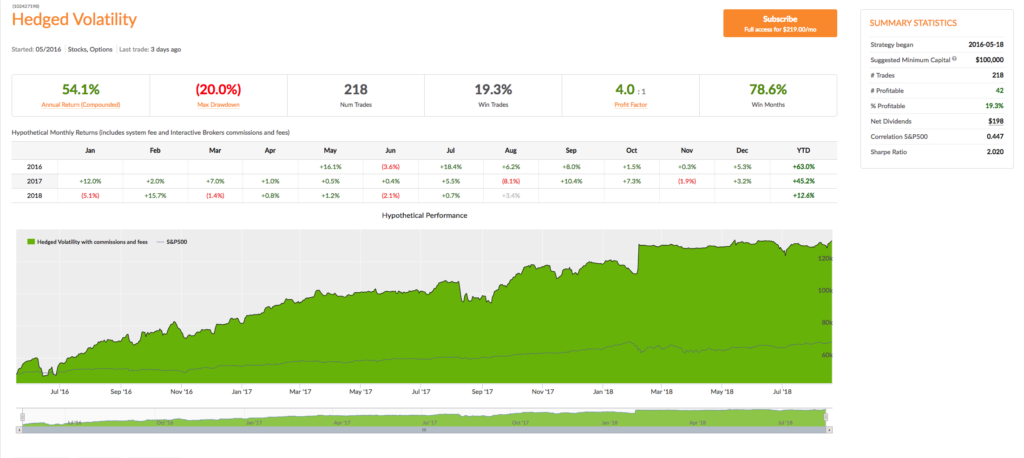
The Hedged Volatility Strategy
Being short regular Volatility ETFs or long Inverse Volatility ETFs are winning strategies…most of the time. The challenge is that when the VIX spikes or when the VIX futures curve is downward sloping instead of upward sloping, very significant losses can occur. Many people have built and back-tested models that attempt to move from long to short to neutral positions in the various Volatility ETFs, but almost all of them have one or both of these very significant flaws: 1) Failure to use “out of sample” back-testing and 2) Failure to protect against “black swan” events.
In this strategy a position and weighting in the appropriate Volatility ETFs are established based on a multi-factor model which always uses out of sample back-testing to determine effectiveness. Volatility Options are always used to protect against significant short-term moves which left unchecked could result in the total loss of one’s portfolio value; these options will usually lose money, but that is a small price to pay for the protection they provide. (Strategies should be scaled at a minimum of 20% to ensure options protection.)
This is a good strategy for IRA accounts in which short selling is not allowed. Long positions in Inverse Volatility ETFs are typically held. Suggested minimum capital: $26,000 (using 20% scaling).
Covered Writes, Covered Wrongs
What is a Covered Call?
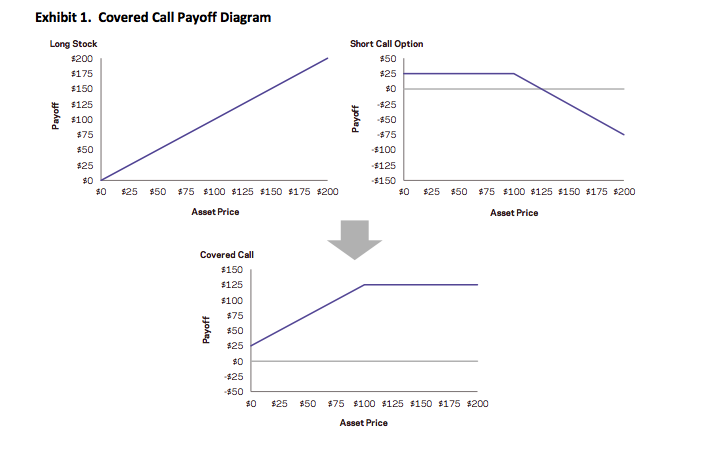
A covered call (or covered write or buy-write) is a long position in a security and a short position in a call option on that security. The diagram below constructs the covered call payoff diagram, including the option premium, at expiration when the call option is written at a $100 strike with a $25 option premium.
Equity index covered calls are an attractive strategy to many investors because they have realized returns not much lower than those of the equity market but with much lower volatility. But investors often do the trade for the wrong reasons: there are a number of myths about covered writes that persist even amongst professional options traders. I have heard most, if not all of them professed by seasons floor traders on the American Stock Exchange and, I confess, I have even used one or two of them myself. Roni Israelov and Larn Nielsen of AQR Capital Management, LLC have done a fine job of elucidating and then dispelling these misunderstandings about the strategy, in their paper Covered Call Strategies: One Fact and Eight Myths, Financial Analysts Journal, Vol. 70, No. 6, 2014.
The Cover Call Strategy and its Benefits for Investors
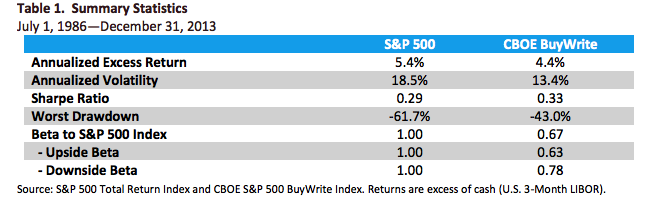
The covered call strategy has generated attention due to its attractive historical risk-adjusted returns. For example, the CBOE S&P 500 BuyWrite Index, the industry-standard covered call benchmark, is commonly described as providing average returns comparable to the S&P 500 Index with approximately two-thirds the volatility, supported by statistics such as those shown below.
The key advantages of the strategy (compared to an outright, delta-one position) include lower volatility, beta and tail risk. As a consequence, the strategy produces higher risk-adjusted rates if return (Sharpe Ratio). Note, too, the beta convexity of the strategy, a topic I cover in this post:
http://jonathankinlay.com/2017/05/beta-convexity/
Although the BuyWrite Index has historically demonstrated similar total returns to the S&P 500, it does so with a reduced beta to the S&P 500 Index. However, it is important to also understand that the BuyWrite Index is more exposed to negative S&P 500 returns than positive returns. This asymmetric relationship to the S&P 500 is consistent with its payoff characteristics and results from the fact that a covered call strategy sells optionality. What this means in simple terms is that while drawdowns are somewhat mitigated by the revenue associated with call writing, the upside is capped by those same call options.
Understandably, a strategy that produces equity-like return with lower beta and lower risk attracts considerable attention from investors. According to Moringstar, growth in assets under management in covered call strategies has been over 25% per year over the 10 years through June 2014 with over $45 billion currently invested.
Myths about the Covered Call Strategy
Many option strategies are the subject of investor myths, partly, I suppose, because option strategies are relatively complicated and entail risks in several dimensions. So it is quite easy for investors to become confused. Simple anecdotes are attractive because they appear to cut through the complexity with an easily understood metaphor, but they can often be misleading. An example is the widely-held view – even amongst professional option traders – is that selling volatility via strangles is a less risk approach than selling at-the-money straddles. Intuitively, this makes sense: why wouldn’t selling straddles that have strike prices (far) away from the current spot price be less risky than selling straddles that have strike prices close to the spot price? But, in fact, it turns out that selling straddles is the less risky the two strategies – see this post for details:
http://jonathankinlay.com/2016/11/selling-volatility/
Likewise, the covered call strategy is subject to a number of “urban myths”, that turn out to be unfounded:
Myth 1: Risk exposure is described by the payoff diagram
That is only true at expiration. Along the way, the positions will be marked-to-market and may produce a substantially different payoff if the trade is terminated early. The same holds true for a zero-coupon bond – we know the terminal value for certain, but there can be considerable variation in the value of the asset from day to day.
Myth 2: Covered calls provide downside protection
This is partially true, but only in a very limited sense. Unlike a long option hedge, the “protection” in a buy-write strategy is limited to only the premium collected on the option sale, a relatively modest amount in most cases. Consider a covered call position on a $100 stock with a $10 at-the-money call premium. The covered call can potentially lose $90 and the long call option can lose $10. Each position has the same 50% exposure to the stock, but the covered call’s downside risk is disproportionate to its stock exposure. This is consistent with the covered call’s realized upside and downside betas as discussed earlier.
Myth 3: Covered calls generate income.
Remember that income is revenue minus costs.
It is true that option selling generates positive cash flow, but this incorrectly leads investors to the conclusion that covered calls generate investment income. Just as is the case with bond issuance, the revenue generated from selling the call option is not income (though, like income, the cash flows received from selling options are considered taxable for many investors). In order for there to be investment income or earnings, the option must be sold at a favorable price – the option’s implied volatility needs to be higher than the stock’s expected volatility.
Myth 4: Covered calls on high-volatility stocks and/or shorter-dated options provide higher yield.
Though true that high volatility stocks and short-dated options command higher annualized premiums, insurance on riskier assets should rationally command a higher premium and selling insurance more often per year should provide higher annual premiums. However, these do not equate to higher net income or yield. For instance, if options are properly priced (e.g., according to the Black-Scholes pricing model), then selling 12 at-the-money options will generate approximately 3.5 times the cash flow of selling a single annual option, but this does not unequivocally translate into higher net profits as discussed earlier. Assuming fairly priced options, higher revenue is not necessarily a mechanism for increasing investment income.
The key point here is that what matters is value, not price. In other words, expected investment profits are generated by the option’s richness, not the option’s price. For example, if you want to short a stock with what you consider to be a high valuation, then the goal is not to find a stock with a high price, but rather one that is overpriced relative to its fundamental value. The same principle applies to options. It is not appropriate to seek an option with a high price or other characteristics associated with high prices. Investors must instead look for options that are expensive relative to their fundamental value. Put another way, the investor should seek out options trading at a higher implied volatility than the likely futures realized volatility over the life of the option.
Myth 5: Time decay of options written works in your favor.
While it is true that the value of an option declines over time as it approaches expiration, that is not the whole story. In fact an option’s expected intrinsic value increases as the underlying security realizes volatility. What matters is whether the realized volatility turns out to be lower than the volatility baked into the option price – the implied volatility. In truth, an option’s time decay only works in the seller’s favor if the option is initially priced expensive relative to its fundamental value. If the option is priced cheaply, then time decay works very much against the seller.
Myth 6: Covered calls are appropriate if you have a neutral to moderately bullish view.
This myth is an over-simplification. In selling a call option you are expressing a view, not only on the future prospects for the stock, but also on its likely future volatility. It is entirely possible that the stock could stall (or even decline) and yet the value of the option you have sold rises due, say, to takeover rumors. A neutral view on the stock may imply a belief that the security price will not move far from its current price rather than its expected return is zero. If so, then a short straddle position is a way to express that view — not a covered call — because, in this case, no active position should be taken in the security.
Myth 7: Overwriting pays you for doing what you were going to do anyway
This myth is typically posed as the following question: if you have a price target for selling a stock you own, why not get paid to write a call option struck at that price target?
In fact this myth exposes the critical difference between a plan and a contractual obligation. If the former case, suppose that the stock hits your target price very much more quickly than you had anticipated, perhaps as a result of a new product announcement that you had not anticipated at the time you set your target. In those circumstances you might very well choose to maintain your long position and revise your price target upwards. This is an example of a plan – a successful one – that can be adjusted to suit circumstances as they change.
A covered call strategy is an obligation, rather than a plan. You have pre-sold the stock at the target price and, in the above scenario, you cannot change your mind in order to benefit from additional potential upside in the stock.
In other words, with a covered call strategy you have monetized the optionality that is inherent in any plan and turned it into a contractual obligation in exchange for a fee.
Myth 8: Overwriting allows you to buy a stock at a discounted price.
Here is how this myth is typically framed: if a stock that you would like to own is currently priced at $100 and that you think is currently expensive, you can act on that opinion by selling a naked put option at a $95 strike price and collect a premium of say $1. Then, if the price subsequently declines below the strike price, the option will likely be exercised thus requiring you to buy the stock for $95. Including the $1 premium, you effectively buy the stock at a 6% discount. If the option is not exercised you keep the premium as income. So, this type of outcome for selling naked put options may also lead you to conclude that the equivalent covered call strategy makes sense and is valuable.
But this argument is really a sleight of hand. In our example above, if the option is exercised, then when you buy the stock for $95 you won’t care what the stock price was when you sold the option. What matters is the stock price on the date the option was exercised. If the stock price dropped all the way down to $80, the $95 purchase price no longer seems like a discount. Your P&L will show a mark-to-market loss of $14 ($95 – $80 – $1). The initial stock price is irrelevant and the $1 premium hardly helps.
Conclusion: How to Think About the Covered Call Strategy
Investors should ignore the misleading storytelling about obtaining downside buffers and generating income. A covered call strategy only generates income to the extent that any other strategy generates income, by buying or selling mispriced securities or securities with an embedded risk premium. Avoid the temptation to overly focus on payoff diagrams. If you believe the index will rise and implied volatilities are rich, a covered call is a step in the right direction towards expressing that view.
If you have no view on implied volatility, there is no reason to sell options, or covered calls
Aby znaleźć legalne kasyna online w Polsce, odwiedź stronę pl.kasynopolska10.com/legalne-kasyna/, partnera serwisu recenzującego kasyna online – KasynoPolska10.
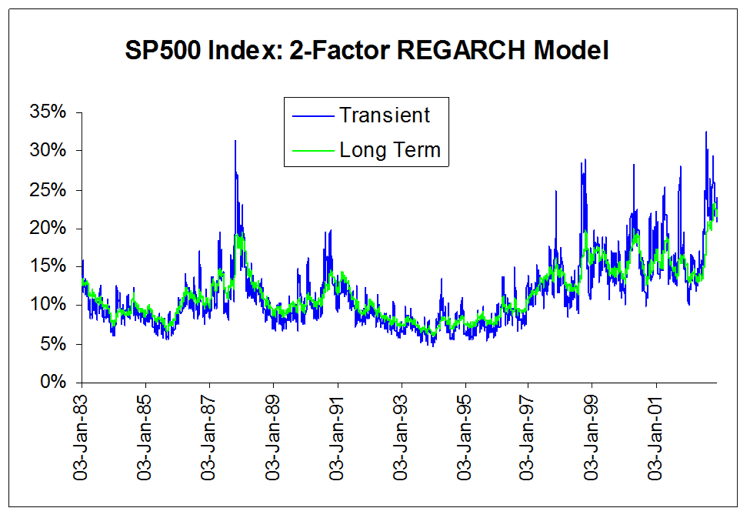
Range-Based EGARCH Option Pricing Models (REGARCH)
The research in this post and the related paper on Range Based EGARCH Option pricing Models is focused on the innovative range-based volatility models introduced in Alizadeh, Brandt, and Diebold (2002) (hereafter ABD). We develop new option pricing models using multi-factor diffusion approximations couched within this theoretical framework and examine their properties in comparison with the traditional Black-Scholes model.
The two-factor version of the model, which I have applied successfully in various option arbitrage strategies, encapsulates the intuively appealing idea of a trending long term mean volatility process, around which oscillates a mean-reverting, transient volatility process. The option pricing model also incorporates asymmetry/leverage effects and well as correlation effects between the asset return and volatility processes, which results in a volatility skew.
The core concept behind Range-Based Exponential GARCH model is Log-Range estimator discussed in an earlier post on volatility metrics, which contains a lengthy exposition of various volatility estimators and their properties. (Incidentally, for those of you who requested a copy of my paper on Estimating Historical Volatility, I have updated the post to include a link to the pdf).
We assume that the log stock price s follows a drift-less Brownian motion ds = sdW. The volatility of daily log returns, denoted h= s/sqrt(252), is assumed constant within each day, at ht from the beginning to the end of day t, but is allowed to change from one day to the next, from ht at the end of day t to ht+1 at the beginning of day t+1. Under these assumptions, ABD show that the log range, defined as:
is to a very good approximation distributed as
where N[m; v] denotes a Gaussian distribution with mean m and variance v. The above equation demonstrates that the log range is a noisy linear proxy of log volatility ln ht. By contrast, according to the results of Alizadeh, Brandt,and Diebold (2002), the log absolute return has a mean of 0.64 + ln ht and a variance of 1.11. However, the distribution of the log absolute return is far from Gaussian. The fact that both the log range and the log absolute return are linear log volatility proxies (with the same loading of one), but that the standard deviation of the log range is about one-quarter of the standard deviation of the log absolute return, makes clear that the range is a much more informative volatility proxy. It also makes sense of the finding of Andersen and Bollerslev (1998) that the daily range has approximately the same informational content as sampling intra-daily returns every four hours.
Except for the model of Chou (2001), GARCH-type volatility models rely on squared or absolute returns (which have the same information content) to capture variation in the conditional volatility ht. Since the range is a more informative volatility proxy, it makes sense to consider range-based GARCH models, in which the range is used in place of squared or absolute returns to capture variation in the conditional volatility. This is particularly true for the EGARCH framework of Nelson (1990), which describes the dynamics of log volatility (of which the log range is a linear proxy).
ABD consider variants of the EGARCH framework introduced by Nelson (1990). In general, an EGARCH(1,1) model performs comparably to the GARCH(1,1) model of Bollerslev (1987). However, for stock indices the in-sample evidence reported by Hentschel (1995) and the forecasting performance presented by Pagan and Schwert (1990) show a slight superiority of the EGARCH specification. One reason for this superiority is that EGARCH models can accommodate asymmetric volatility (often called the “leverage effect,” which refers to one of the explanations of asymmetric volatility), where increases in volatility are associated more often with large negative returns than with equally large positive returns.
The one-factor range-based model (REGARCH 1) takes the form:
where the returns process Rt is conditionally Gaussian: Rt ~ N[0, ht2]
and the process innovation is defined as the standardized deviation of the log range from its expected value:
Following Engle and Lee (1999), ABD also consider multi-factor volatility models. In particular, for a two-factor range-based EGARCH model (REGARCH2), the conditional volatility dynamics) are as follows:
and
where ln qt can be interpreted as a slowly-moving stochastic mean around which log volatility ln ht makes large but transient deviations (with a process determined by the parameters kh, fh and dh).
The parameters q, kq, fq and dq determine the long-run mean, sensitivity of the long run mean to lagged absolute returns, and the asymmetry of absolute return sensitivity respectively.
The intuition is that when the lagged absolute return is large (small) relative to the lagged level of volatility, volatility is likely to have experienced a positive (negative) innovation. Unfortunately, as we explained above, the absolute return is a rather noisy proxy of volatility, suggesting that a substantial part of the volatility variation in GARCH-type models is driven by proxy noise as opposed to true information about volatility. In other words, the noise in the volatility proxy introduces noise in the implied volatility process. In a volatility forecasting context, this noise in the implied volatility process deteriorates the quality of the forecasts through less precise parameter estimates and, more importantly, through less precise estimates of the current level of volatility to which the forecasts are anchored.
read more…
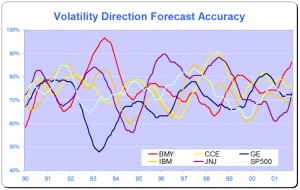
On Testing Direction Prediction Accuracy
As regards the question of forecasting accuracy discussed in the paper on Forecasting Volatility in the S&P 500 Index, there are two possible misunderstandings here that need to be cleared up. These arise from remarks by one commentator as follows:
“An above 50% vol direction forecast looks good,.. but “direction” is biased when working with highly skewed distributions! ..so it would be nice if you could benchmark it against a simple naive predictors to get a feel for significance, -or- benchmark it with a trading strategy and see how the risk/return performs.”
(i) The first point is simple, but needs saying: the phrase “skewed distributions” in the context of volatility modeling could easily be misconstrued as referring to the volatility skew. This, of course, is used to describe to the higher implied vols seen in the Black-Scholes prices of OTM options. But in the Black-Scholes framework volatility is constant, not stochastic, and the “skew” referred to arises in the distribution of the asset return process, which has heavier tails than the Normal distribution (excess Kurtosis and/or skewness). I realize that this is probably not what the commentator meant, but nonetheless it’s worth heading that possible misunderstanding off at the pass, before we go on.
(ii) I assume that the commentator was referring to the skewness in the volatility process, which is characterized by the LogNormal distribution. But the forecasting tests referenced in the paper are tests of the ability of the model to predict the direction of volatility, i.e. the sign of the change in the level of volatility from the current period to the next period. Thus we are looking at, not a LogNormal distribution, but the difference in two LogNormal distributions with equal mean – and this, of course, has an expectation of zero. In other words, the expected level of volatility for the next period is the same as the current period and the expected change in the level of volatility is zero. You can test this very easily for yourself by generating a large number of observations from a LogNormal process, taking the difference and counting the number of positive and negative changes in the level of volatility from one period to the next. You will find, on average, half the time the change of direction is positive and half the time it is negative.
For instance, the following chart shows the distribution of the number of positive changes in the level of a LogNormally distributed random variable with mean and standard deviation of 0.5, for a sample of 1,000 simulations, each of 10,000 observations. The sample mean (5,000.4) is very close to the expected value of 5,000.
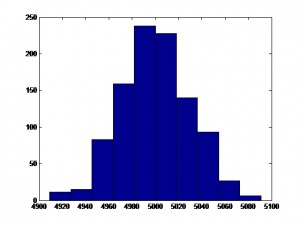
So, a naive predictor will forecast volatility to remain unchanged for the next period and by random chance approximately half the time volatility will turn out to be higher and half the time it will turn out to be lower than in the current period. Hence the default probability estimate for a positive change of direction is 50% and you would expect to be right approximately half of the time. In other words, the direction prediction accuracy of the naive predictor is 50%. This, then, is one of the key benchmarks you use to assess the ability of the model to predict market direction. That is what test statistics like Theil’s-U does – measures the performance relative to the naive predictor. The other benchmark we use is the change of direction predicted by the implied volatility of ATM options.
In this context, the model’s 61% or higher direction prediction accuracy is very significant (at the 4% level in fact) and this is reflected in the Theil’s-U statistic of 0.82 (lower is better). By contrast, Theil’s-U for the Implied Volatility forecast is 1.46, meaning that IV is a much worse predictor of 1-period-ahead changes in volatility than the naive predictor.
On its face, it is because of this exceptional direction prediction accuracy that a simple strategy is able to generate what appear to be abnormal returns using the change of direction forecasts generated by the model, as described in the paper. In fact, the situation is more complicated than that, once you introduce the concept of a market price of volatility risk.
Modeling Asset Volatility
I am planning a series of posts on the subject of asset volatility and option pricing and thought I would begin with a survey of some of the central ideas. The attached presentation on Modeling Asset Volatility sets out the foundation for a number of key concepts and the basis for the research to follow.
Perhaps the most important feature of volatility is that it is stochastic rather than constant, as envisioned in the Black Scholes framework. The presentation addresses this issue by identifying some of the chief stylized facts about volatility processes and how they can be modelled. Certain characteristics of volatility are well known to most analysts, such as, for instance, its tendency to “cluster” in periods of higher and lower volatility. However, there are many other typical features that are less often rehearsed and these too are examined in the presentation.
Long Memory
For example, while it is true that GARCH models do a fine job of modeling the clustering effect they typically fail to capture one of the most important features of volatility processes – long term serial autocorrelation. In the typical GARCH model autocorrelations die away approximately exponentially, and historical events are seen to have little influence on the behaviour of the process very far into the future. In volatility processes that is typically not the case, however: autocorrelations die away very slowly and historical events may continue to affect the process many weeks, months or even years ahead.
There are two immediate and very important consequences of this feature. The first is that volatility processes will tend to trend over long periods – a characteristic of Black Noise or Fractionally Integrated processes, compared to the White Noise behavior that typically characterizes asset return processes. Secondly, and again in contrast with asset return processes, volatility processes are inherently predictable, being conditioned to a significant degree on past behavior. The presentation considers the fractional integration frameworks as a basis for modeling and forecasting volatility.
Mean Reversion vs. Momentum
A puzzling feature of much of the literature on volatility is that it tends to stress the mean-reverting behavior of volatility processes. This appears to contradict the finding that volatility behaves as a reinforcing process, whose long-term serial autocorrelations create a tendency to trend. This leads to one of the most important findings about asset processes in general, and volatility process in particular: i.e. that the assets processes are simultaneously trending and mean-reverting. One way to understand this is to think of volatility, not as a single process, but as the superposition of two processes: a long term process in the mean, which tends to reinforce and trend, around which there operates a second, transient process that has a tendency to produce short term spikes in volatility that decay very quickly. In other words, a transient, mean reverting processes inter-linked with a momentum process in the mean. The presentation discusses two-factor modeling concepts along these lines, and about which I will have more to say later.
Cointegration
One of the most striking developments in econometrics over the last thirty years, cointegration is now a principal weapon of choice routinely used by quantitative analysts to address research issues ranging from statistical arbitrage to portfolio construction and asset allocation. Back in the late 1990’s I and a handful of other researchers realized that volatility processes exhibited very powerful cointegration tendencies that could be harnessed to create long-short volatility strategies, mirroring the approach much beloved by equity hedge fund managers. In fact, this modeling technique provided the basis for the Caissa Capital volatility fund, which I founded in 2002. The presentation examines characteristics of multivariate volatility processes and some of the ideas that have been proposed to model them, such as FIGARCH (fractionally-integrated GARCH).
Dispersion Dynamics
Finally, one topic that is not considered in the presentation, but on which I have spent much research effort in recent years, is the behavior of cross-sectional volatility processes, which I like to term dispersion. It turns out that, like its univariate cousin, dispersion displays certain characteristics that in principle make it highly forecastable. Given an appropriate model of dispersion dynamics, the question then becomes how to monetize efficiently the insight that such a model offers. Again, I will have much more to say on this subject, in future.
Forecasting Volatility in the S&P500 Index
Several people have asked me for copies of this research article, which develops a new theoretical framework, the ARFIMA-GARCH model as a basis for forecasting volatility in the S&P 500 Index. I am in the process of updating the research, but in the meantime a copy of the original paper is available here
In this analysis we are concerned with the issue of whether market forecasts of volatility, as expressed in the Black-Scholes implied volatilities of at-the-money European options on the S&P500 Index, are superior to those produced by a new forecasting model in the GARCH framework which incorporates long-memory effects. The ARFIMA-GARCH model, which uses high frequency data comprising 5-minute returns, makes volatility the subject process of interest, to which innovations are introduced via a volatility-of-volatility (kurtosis) process. Despite performing robustly in- and out-of-sample, an encompassing regression indicates that the model is unable to add to the information already contained in market forecasts. However, unlike model forecasts, implied volatility forecasts show evidence of a consistent and substantial bias. Furthermore, the model is able to correctly predict the direction of volatility approximately 62% of the time whereas market forecasts have very poor direction prediction ability. This suggests that either option markets may be inefficient, or that the option pricing model is mis-specified. To examine this hypothesis, an empirical test is carried out in which at-the-money straddles are bought or sold (and delta-hedged) depending on whether the model forecasts exceed or fall below implied volatility forecasts. This simple strategy generates an annual compound return of 18.64% over a four year out-of-sample period, during which the annual return on the S&P index itself was -7.24%. Our findings suggest that, over the period of analysis, investors required an additional risk premium of 88 basis points of incremental return for each unit of volatility risk.
Riders on the Storm
The Worst Volatility Scare for Years
February 2018 was an insane month for stocks, wrote CNN:
A profound inflation scare. Not one but two 1,000-point plunges for the Dow. And a powerful comeback that almost went straight back up.
The CNN story-line continues:
The Dow plummeted more than 3,200 points, or 12%, in just two weeks. Then stocks raced back to life, at one point recovering about three-quarters of those losses.
Fittingly, February ended with more drama. The Dow tumbled 680 points during the month’s final two days, leaving it down about 1,600 points from the record high in late January.
The headline in the Financial Times was a little more nuanced, focusing on the impact of the market turmoil on quant hedge funds:
Quant Funds Get Trashed
The FT reported:
Computer-driven, trend-following hedge funds are heading for their worst month in nearly 17 years after getting whipsawed when the stock market’s steady soar abruptly reversed into one of the quickest corrections in history earlier in February.
The carnage amongst hedge funds was widespread, according to the article:
Société Générale’s CTA index is down 5.55 per cent this month, even after the recent market rebound, making it the worst period for these systematic hedge funds since November 2001.
Man AHL’s $1.1bn Diversified fund lost almost 10 per cent in the month to February 16, while the London investment firm’s AHL Evolution and Alpha funds were down about 4-5 per cent over the same period. The flagship funds of GAM’s Cantab Capital, Systematica and Winton lost 9.5 per cent, 7.2 per cent and 4.6 per cent* respectively between the start of the month and February 16. Aspect Capital’s Diversified Fund dropped 9.5 per cent in the month to February 20, while a trend-following fund run by Lynx Asset Management slumped 12.7 per cent. A leveraged version of the same fund tumbled 18.8 per cent. One of the other big victims is Roy Niederhoffer, whose fund lost 21.1 per cent in the month to February 20.
Painful reading, indeed.
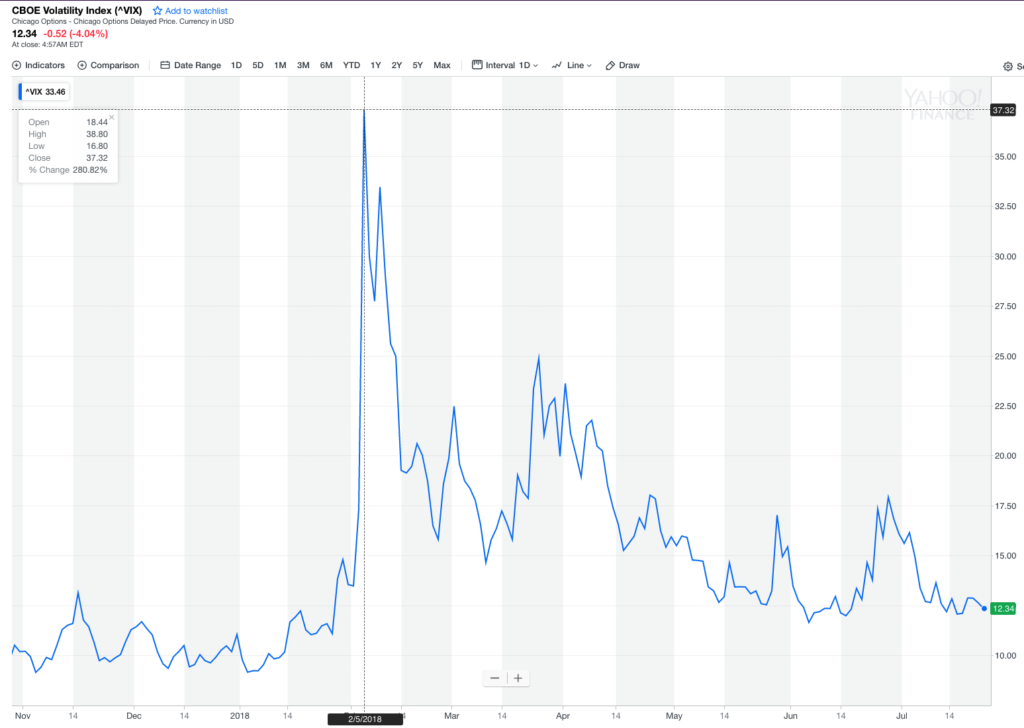
Traders conditioned to a state of somnambulance were shocked by the ferocity of the volatility spike, as the CBOE VIX index soared by over 200% in a single day, reaching a high of over 38 on Feb 5th:
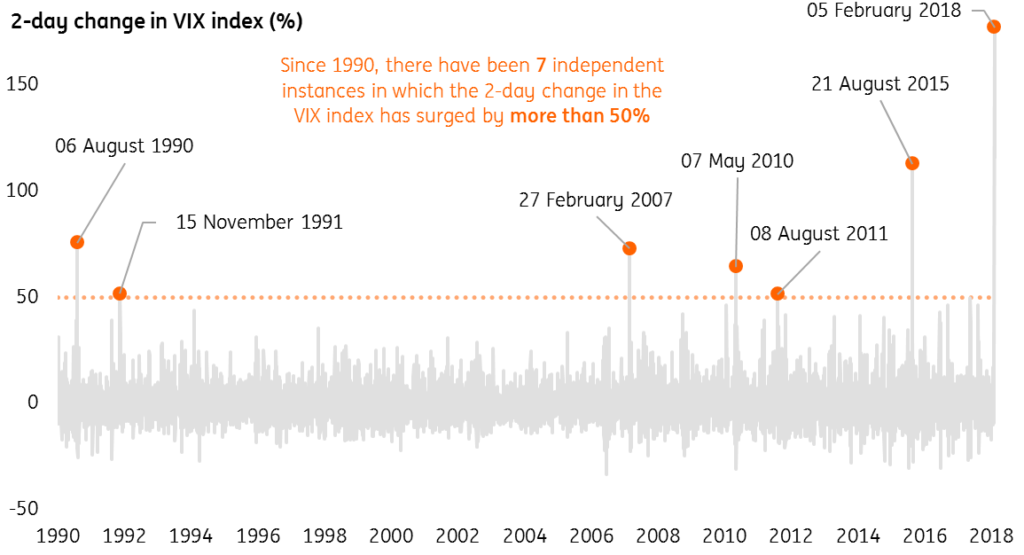
Indeed, this turned out to be the largest ever two-day increase in the history of the index:
This Quant Strategy Made 27% In February Alone
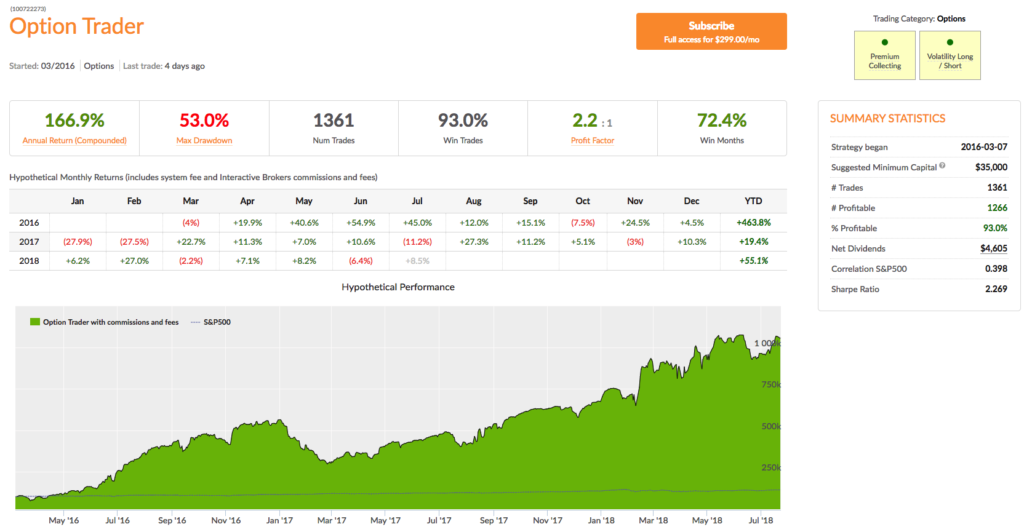
So, for a quant-driven options strategy that is typically a premium seller, February must surely have been a disaster, if not a total wipe-out. Not quite. On the contrary, our Option Trader strategy made a massive gain of 27% for the month. As a result strategy performance is now running at over 55% for 2018 YTD, while maintaining a Sharpe Ratio of 2.23.
You can tell that the strategy has a tendency to collect option premiums, not only because the strategy description says as much, but also from the observation that over 90% of strategy trades have been profitable – one of the defining characteristics of volatility strategies that are short-Vega, long-Theta. The theory is that such strategies make money most of the time, but then give it all back (and more) when volatility inevitably spikes. While that is generally true, in my experience, that clearly didn’t occur here. So what’s the story?
One of the advantages of our Algo Trading Platform is that it not only reports in detail the live performance of our strategies, but it also reveals the actual trades on the site (typically delayed by 24-72 hours). A review of the trades made by the Option Trader strategy from the end of January though early February indicates a strongly bullish bias, with short put trades in stocks such as Netflix, Inc. (NFLX), Shopify Inc. (SHOP), The Goldman Sachs Group, Inc. (GS) and Facebook, Inc. (FB), coupled with short call trades in VIX ETF products such as ProShares Ultra VIX Short-Term Futures (UVXY) and iPath S&P 500 VIX ST Futures ETN (VXX). As volatility began to spike on 2/5, more calls were sold at increasingly fat premiums in several of the VIX Index ETFs. These short volatility positions were later hedged with long trades in the underlying ETFs and, over time, both the hedges and the original option sales proved highly profitable. In other words, the extremely high levels of volatility enabled the strategy to profit on both legs of the trade, a highly unusual occurrence. Meanwhile, while it was hedging its bets in the VIX ETF option trades, the strategy was becoming increasingly aggressive in the single stocks sector, taking outright long positions in Baidu, Inc. (BIDU), Align Technology, Inc. (ALGN), Netflix, Inc. (NFLX) and others, just as they became trading off their lows in the second week of the month. By around Feb 12th the strategy recognized that the volatility shock had begun to subside and took advantage of the inflated option premia, selling puts across the board, in particular in the technology (Tesla, Inc. (TSLA), NVIDIA Corporation (NVDA)) and retail sectors (GrubHub Inc. (GRUB), Alibaba Group Holding Limited (BABA)) that had suffered especially heavy declines. Many of these trades were closed at a substantial profit within a span of just a few days as the market stabilized and volatility subsided. The strategy broadened the scope of its option selling as the month progressed, initially recovering the entirety of the drawdown it had initially suffered, before going on to register substantial profits on almost every trade.
To summarize:
- Like many other market players, the Volatility Trader strategy was initially caught on the wrong side of the volatility spike and suffered a significant drawdown.
- Instead of liquidating positions, the strategy began hedging aggressively in sectors holding the greatest danger – VIX ETFs, in particular. These trades ultimately proved profitable on both option and hedge legs as the market turned around and volatility collapsed.
- As soon as volatility showed signed of easing, the strategy began making aggressive bets on market stabilization and recovery, taking long positions in some of the most beaten-down stocks and selling puts across the board to capture inflated option premia.
Lesson Learned: Aggressive Defense is the best Options Strategy in a Volatile Market
If there is one lesson above all others to be learned from this case study it is this: that a period of market turmoil is a time of opportunity for option traders, but only if they play aggressively, both in defense and offense. Many traders run scared at times like this and liquidate positions, taking heavy losses in the process that can prove impossible to recover from if, as here, the drawdown is severe. This study shows that by holding one’s nerve and hedging rather than liquidating loss-making positions and then moving aggressively to capitalize on inflated option prices a trader can not only weather the storm but, as in this case, produce exceptional returns.
The key take-away is this: in order to play aggressively you have to have sufficient reserves in the tank to enable you to hold positions rather than liquidate them and, later on, to transition to selling expensive option premiums. The mistake many option traders make is to trade too close to the line in term of margin limits, resulting in a forced liquidation of positions that would otherwise have been profitable.
You can trade the Option Trader strategy live in your own brokerage account – go here for details.