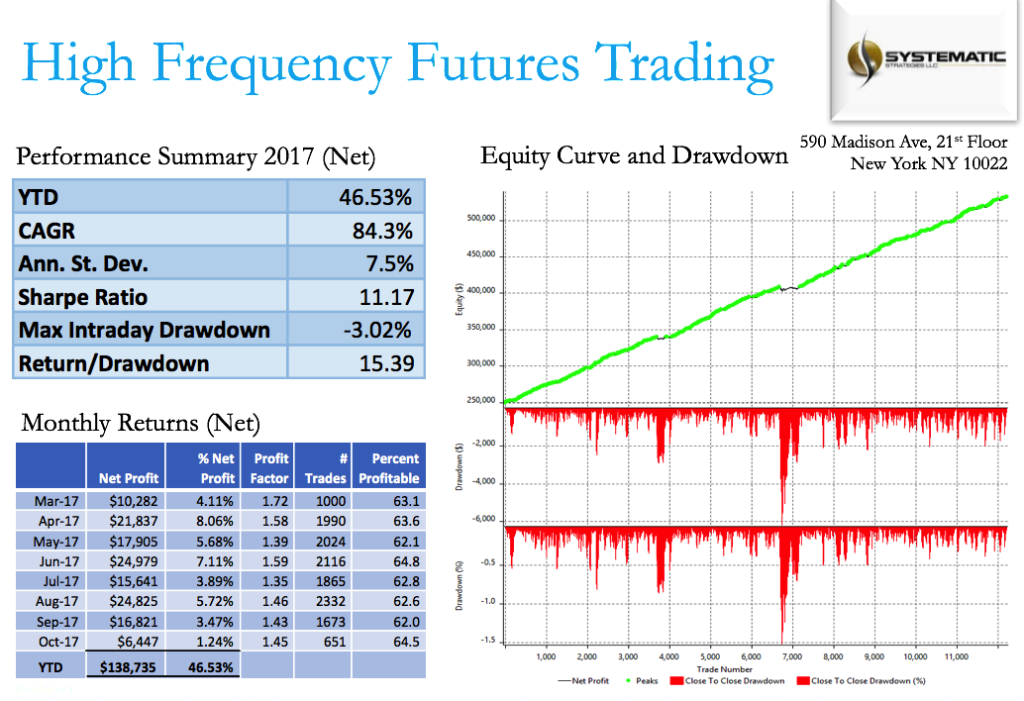
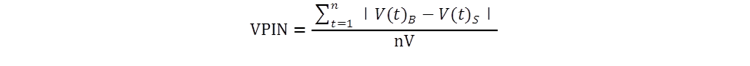Tag: Market Microstructure

Posted on

Measuring Toxic Flow for Trading & Risk Management

A common theme of microstructure modeling is that trade flow is often predictive of market direction.  One concept in particular that has gained traction is flow toxicity, i.e. flow where resting orders tend to be filled more quickly than expected, while aggressive orders rarely get filled at all, due to the participation of informed traders trading against uninformed traders.  The fundamental insight from microstructure research is that the order arrival process is informative of subsequent price moves in general and toxic flow in particular.  This is turn has led researchers to try to measure the probability of informed trading  (PIN).  One recent attempt to model flow toxicity, the Volume-Synchronized Probability of Informed Trading (VPIN)metric, seeks to estimate PIN based on volume imbalance and trade intensity.  A major advantage of this approach is that it does not require the estimation of unobservable parameters and, additionally, updating VPIN in trade time rather than clock time improves its predictive power.  VPIN has potential applications both in high frequency trading strategies, but also in risk management, since highly toxic flow is likely to lead to the withdrawal of liquidity providers, setting up the conditions for a flash-crash” type of market breakdown.

The procedure for estimating VPIN is as follows.  We begin by grouping sequential trades into equal volume buckets of size V.  If the last trade needed to complete a bucket was for a size greater than needed, the excess size is given to the next bucket.  Then we classify trades within each bucket into two volume groups:  Buys (V(t)B) and Sells (V(t)S), with V = V(t)B + V(t)S
The Volume-Synchronized Probability of Informed Trading is then derived as:

risk management

Typically one might choose to estimate VPIN using a moving average over n buckets, with n being in the range of 50 to 100.

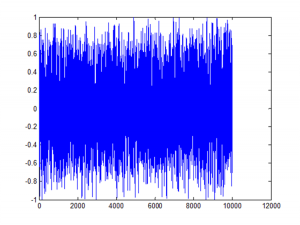
Another related statistic of interest is the single-period signed VPIN. This will take a value of between -1 and =1, depending on the proportion of buying to selling during a single period t.

Toxic Flow

Fig 1. Single-Period Signed VPIN for the ES Futures Contract

It turns out that quote revisions condition strongly on the signed VPIN. For example, in tests of the ES futures contract, we found that the change in the midprice from one volume bucket the next  was highly correlated to the prior bucket’s signed VPIN, with a coefficient of 0.5.  In other words, market participants offering liquidity will adjust their quotes in a way that directly reflects the direction and intensity of toxic flow, which is perhaps hardly surprising.

Of greater interest is the finding that there is a small but statistically significant dependency of price changes, as measured by first buy (sell) trade price to last sell (buy) trade price, on the prior period’s signed VPIN.  The correlation is positive, meaning that strongly toxic flow in one direction has a tendency  to push prices in the same direction during the subsequent period. Moreover, the single period signed VPIN turns out to be somewhat predictable, since its autocorrelations are statistically significant at two or more lags.  A simple linear auto-regression ARMMA(2,1) model produces an R-square of around 7%, which is small, but statistically significant.

A more useful model, however , can be constructed by introducing the idea of Markov states and allowing the regression model to assume different parameter values (and error variances) in each state.  In the Markov-state framework, the system transitions from one state to another with conditional probabilities that are estimated in the model.

SSALGOTRADING AD

An example of such a model  for the signed VPIN in ES is shown below. Note that the model R-square is over 27%, around 4x larger than for a standard linear ARMA model.

We can describe the regime-switching model in the following terms.  In the regime 1 state  the model has two significant autoregressive terms and one significant moving average term (ARMA(2,1)).  The AR1 term is large and positive, suggesting that trends in VPIN tend to be reinforced from one period to the next. In other words, this is a momentum state. In the regime 2 state the AR2 term is not significant and the AR1 term is large and negative, suggesting that changes in VPIN in one period tend to be reversed in the following period, i.e. this is a mean-reversion state.

The state transition probabilities indicate that the system is in mean-reversion mode for the majority of the time, approximately around 2 periods out of 3.  During these periods, excessive flow in one direction during one period tends to be corrected in the
ensuring period.  But in the less frequently occurring state 1, excess flow in one direction tends to produce even more flow in the same direction in the following period.  This first state, then, may be regarded as the regime characterized by toxic flow.

Markov State Regime-Switching Model

Markov Transition Probabilities

P(.|1)       P(.|2)

P(1|.)        0.54916      0.27782

P(2|.)       0.45084      0.7221

Regime 1:

AR1           1.35502    0.02657   50.998        0

AR2         -0.33687    0.02354   -14.311        0

MA1          0.83662    0.01679   49.828        0

Error Variance^(1/2)           0.36294     0.0058

Regime 2:

AR1      -0.68268    0.08479    -8.051        0

AR2       0.00548    0.01854    0.296    0.767

MA1     -0.70513    0.08436    -8.359        0

Error Variance^(1/2)           0.42281     0.0016

Log Likelihood = -33390.6

Schwarz Criterion = -33445.7

Hannan-Quinn Criterion = -33414.6

Akaike Criterion = -33400.6

Sum of Squares = 8955.38

R-Squared =  0.2753

R-Bar-Squared =  0.2752

Residual SD =  0.3847

Residual Skewness = -0.0194

Residual Kurtosis =  2.5332

Jarque-Bera Test = 553.472     {0}

Box-Pierce (residuals):         Q(9) = 13.9395 {0.124}

Box-Pierce (squared residuals): Q(12) = 743.161     {0}

 

A Simple Trading Strategy

One way to try to monetize the predictability of the VPIN model is to use the forecasts to take directional positions in the ES
contract.  In this simple simulation we assume that we enter a long (short) position at the first buy (sell) price if the forecast VPIN exceeds some threshold value 0.1  (-0.1).  The simulation assumes that we exit the position at the end of the current volume bucket, at the last sell (buy) trade price in the bucket.

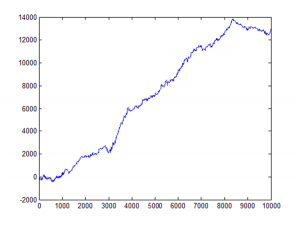
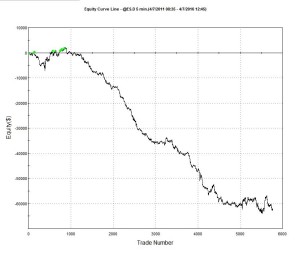
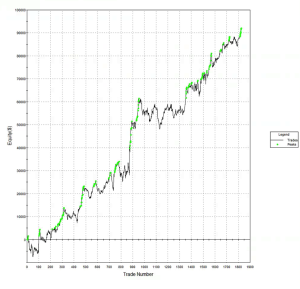
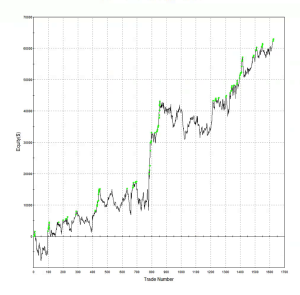
This simple strategy made 1024 trades over a 5-day period from 8/8 to 8/14, 90% of which were profitable, for a total of $7,675 – i.e. around ½ tick per trade.

The simulation is, of course, unrealistically simplistic, but it does give an indication of the prospects for  more realistic version of the strategy in which, for example, we might rest an order on one side of the book, depending on our VPIN forecast.

informed trading

Figure 2 – Cumulative Trade PL

References

Easley, D., Lopez de Prado, M., O’Hara, M., Flow Toxicity and Volatility in a High frequency World, Johnson School Research paper Series # 09-2011, 2011

Easley, D. and M. O‟Hara (1987), “Price, Trade Size, and Information in Securities Markets”, Journal of Financial Economics, 19.

Easley, D. and M. O‟Hara (1992a), “Adverse Selection and Large Trade Volume: The Implications for Market Efficiency”,
Journal of Financial and Quantitative Analysis, 27(2), June, 185-208.

Easley, D. and M. O‟Hara (1992b), “Time and the process of security price adjustment”, Journal of Finance, 47, 576-605.

 

Posted on

Master’s in High Frequency Finance

I have been discussing with some potential academic partners the concept for a new graduate program in High Frequency Finance.  The idea is to take the concept of the Computational Finance program developed in the 1990s and update it to meet the needs of students in the 2010s.

The program will offer a thorough grounding in the modeling concepts, trading strategies and risk management procedures currently in use by leading investment banks, proprietary trading firms and hedge funds in US and international financial markets.  Students will also learn the necessary programming and systems design skills to enable them to make an effective contribution as quantitative analysts, traders, risk managers and developers.

I would be interested in feedback and suggestions as to the proposed content of the program.

Posted on

Systematic Futures Trading

In its proprietary trading, Systematic Strategies primary focus in on equity and volatility strategies, both low and high frequency. In futures, the emphasis is on high frequency trading, although we also run one or two lower frequency strategies that have higher capacity, such as the Futures WealthBuilder. The version of WealthBuilder running on the Collective 2 site has performed very well in 2017, with net returns of 30% and a Sharpe Ratio of 3.4:

Futures C2 oct 2017

 

In the high frequency space, our focus is on strategies with very high Sharpe Ratios and low drawdowns. We trade a range of futures products, including equity, fixed income, metals and energy markets. Despite the current low levels of market volatility, these strategies have performed well in 2017:

HFT Futures Oct 2017 (NFA)

Building high frequency strategies with double-digit Sharpe Ratios requires a synergy of computational capability and modeling know-how. The microstructure of futures markets is, of course, substantially different to that of equity or forex markets and the components of the model that include microstructure effects vary widely from one product to another. There can be substantial variations too in the way that time is handled in the model – whether as discrete or continuous “wall time”, in trade time, or some other measure. But some of the simple technical indicators we use – moving averages, for example – are common to many models across different products and markets. Machine learning plays a role in most of our trading strategies, including high frequency.

Here are some relevant blog posts that you may find interesting:

http://jonathankinlay.com/2016/04/high-frequency-trading-equities-vs-futures/

 

http://jonathankinlay.com/2015/05/designing-scalable-futures-strategy/

 

http://jonathankinlay.com/2014/10/day-trading-system-in-vix-futures/

Posted on

High Frequency Trading: Equities vs. Futures

A talented young system developer I know recently reached out to me with an interesting-looking equity curve for a high frequency strategy he had designed in E-mini futures:

Fig1

Pretty obviously, he had been making creative use of the “money management” techniques so beloved by futures systems designers.  I invited him to consider how it would feel to be trading a 1,000-lot E-mini position when the market took a 20 point dive.  A $100,000 intra-day drawdown might make the strategy look a little less appealing.  On the other hand, if you had already made millions of dollars in the strategy, you might no longer care so much.

SSALGOTRADING AD

A more important criticism of money management techniques is that they are typically highly path-dependent:  if you had started your strategy slightly closer to one of the drawdown periods that are almost unnoticeable on the chart, it could have catastrophic consequences for your trading account.  The only way to properly evaluate this, I advised, was to backtest the strategy over many hundreds of thousands of test-runs using Monte Carlo simulation.  That would reveal all too clearly that the risk of ruin was far larger than might appear from a single backtest.

Next, I asked him whether the strategy was entering and exiting passively, by posting bids and offers, or aggressively, by crossing the spread to sell at the bid and buy at the offer.  I had a pretty good idea what his answer would be, given the volume of trades in the strategy and, sure enough he confirmed the strategy was using passive entries and exits.  Leaving to one side the challenge of executing a trade for 1,000 contracts in this way, I instead ask him to show me the equity curve for a single contract in the underlying strategy, without the money-management enhancement. It was still very impressive.

Fig2

 

The Critical Fill Assumptions For Passive Strategies

But there is an underlying assumption built into these results, one that I have written about in previous posts: the fill rate.  Typically in a retail trading platform like Tradestation the assumption is made that your orders will be filled if a trade occurs at the limit price at which the system is attempting to execute.  This default assumption of a 100% fill rate is highly unrealistic.  The system’s orders have to compete for priority in the limit order book with the orders of many thousands of other traders, including HFT firms who are likely to beat you to the punch every time.  As a consequence, the actual fill rate is likely to be much lower: 10% to 20%, if you are lucky.  And many of those fills will be “toxic”:  buy orders will be the last to be filled just before the market  moves lower and sell orders will be the last to get filled just as the market moves higher. As a result, the actual performance of the strategy will be a very long way from the pretty picture shown in the chart of the hypothetical equity curve.

One way to get a handle on the problem is to make a much more conservative assumption, that your limit orders will only get filled when the market moves through them.  This can easily be achieved in a product like Tradestation by selecting the appropriate backtest option:

fig3

 

The strategy performance results often look very different when this much more conservative fill assumption is applied.  The outcome for this system was not at all unusual:

Fig4

 

Of course, the more conservative assumption applied here is also unrealistic:  many of the trading system’s sell orders would be filled at the limit price, even if the market failed to move higher (or lower in the case of a buy order).  Furthermore, even if they were not filled during the bar-interval in which they were issued, many limit orders posted by the system would be filled in subsequent bars.  But the reality is likely to be much closer to the outcome assuming a conservative fill-assumption than an optimistic one.    Put another way:  if the strategy demonstrates good performance under both pessimistic and optimistic fill assumptions there is a reasonable chance that it will perform well in practice, other considerations aside.

An Example of a HFT Equity Strategy

Let’s contrast the futures strategy with an example of a similar HFT strategy in equities.  Under the optimistic fill assumption the equity curve looks as follows:

Fig5

Under the more conservative fill assumption, the equity curve is obviously worse, but the strategy continues to produce excellent returns.  In other words, even if the market moves against the system on every single order, trading higher after a sell order is filled, or lower after a buy order is filled, the strategy continues to make money.

Fig6

Market Microstructure

There is a fundamental reason for the discrepancy in the behavior of the two strategies under different fill scenarios, which relates to the very different microstructure of futures vs. equity markets.   In the case of the E-mini strategy the average trade might be, say, $50, which is equivalent to only 4 ticks (each tick is worth $12.50).  So the average trade: tick size ratio is around 4:1, at best.  In an equity strategy with similar average trade the tick size might be as little as 1 cent.  For a futures strategy, crossing the spread to enter or exit a trade more than a handful of times (or missing several limit order entries or exits) will quickly eviscerate the profitability of the system.  A HFT system in equities, by contrast, will typically prove more robust, because of the smaller tick size.

Of course, there are many other challenges to high frequency equity trading that futures do not suffer from, such as the multiplicity of trading destinations.  This means that, for instance, in a consolidated market data feed your system is likely to see trading opportunities that simply won’t arise in practice due to latency effects in the feed.  So the profitability of HFT equity strategies is often overstated, when measured using a consolidated feed.  Futures, which are traded on a single exchange, don’t suffer from such difficulties.  And there are a host of other differences in the microstructure of futures vs equity markets that the analyst must take account of.  But, all that understood, in general I would counsel that equities make an easier starting point for HFT system development, compared to futures.