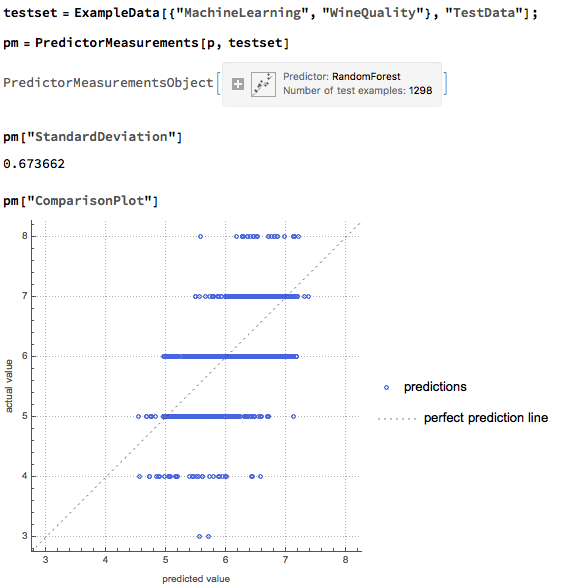
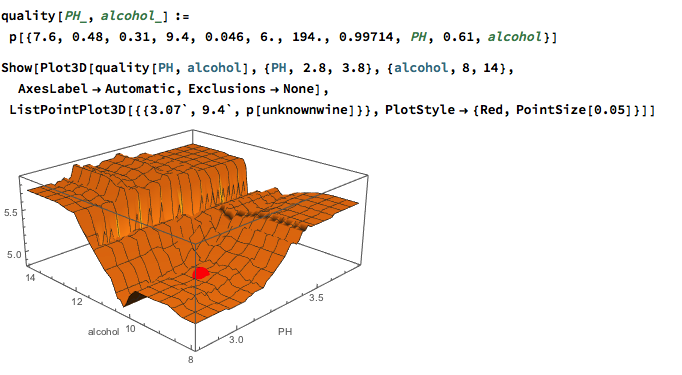
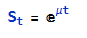Tag: Mathematica

Posted on

Python vs. Wolfram Language

Python vs. Wolfram Language

As an avid user of both Python and Wolfram Language for technical computing, I’m often asked how they compare. Python’s strengths as an open-source language are clear:

  • Ubiquity – With millions of users, Python has become ubiquitous across fields like data science, ML engineering, web development, and scientific research. This massive adoption fuels continuous enhancement of its tools.
  • Comprehensive capabilities – Python’s expansive ecosystem of 200,000+ libraries spans everything from numerical computing to web frameworks to industrial automation. It is a versatile, widely-supported language for building end-to-end applications.
  • Approachability – Python’s straightforward syntax, multitude of online resources, and abundance of machine learning libraries like TensorFlow and PyTorch make it highly accessible for new programmers and non-CS domain experts alike.
  • Interoperability – Python integrates smoothly with everything from SQL and NoSQL databases to enterprise IT environments and microcontrollers like Raspberry Pi. This flexibility enables diverse production deployments.


In summary, Python offers benefits in ubiquity, breadth, approachability, and seamless interoperability with external systems. Together, they show the value of domain-specific and general-purpose languages for tackling modern analytics and engineering challenges.

However, while Python is a versatile, open-source language popular among developers, the Wolfram Language offers some unique advantages:

Powerful Symbolic Capabilities

One of the most powerful aspects of the Wolfram Language is its unparalleled symbolic manipulation abilities for mathematical computation. Operations like symbolic integration, solving equations analytically, theorem proving, model simplification and more are built deeply into the language in a way no other programming language matches. Python can conduct numeric computation and data analysis well, but does not have this domain of symbolic capabilities natively.

For any usage involving abstract mathematical development, derivation of analytical results, or formal proofs, the symbolic nature of the Wolfram Language is a major differentiator.


Wolfram Notebooks

offer notable advantages over Jupyter notebooks in Python:

  • More visual appeal – The Wolfram notebooks produce beautifully typeset output and publication-ready visualizations by default, whereas Jupyter’s output is more basic.
  • Greater configurability – Wolfram’s notebooks allow extensive styling, templating, and customization of content for different applications. Jupyter also enables some configuration, but not to the same degree.
  • Tighter integration – The Wolfram notebooks leverage the language’s underlying functions and capabilities more fluidly since it’s one integrated environment. Jupyter interfaces well with Python but there is still some separation.
  • Interactivity – Wolfram notebooks support advanced interactivity through Manipulate/Animate and instant visual output.

    Overall, while Jupyter notebooks are hugely popular among Python developers and enable great functionality, Wolfram’s notebook solution stands out as more robust, customizable, and visually polished. The tight integration with the Wolfram Language and computational capabilities augments interactive analysis in a way Jupyter can’t match.

Integrated Knowledge and Data

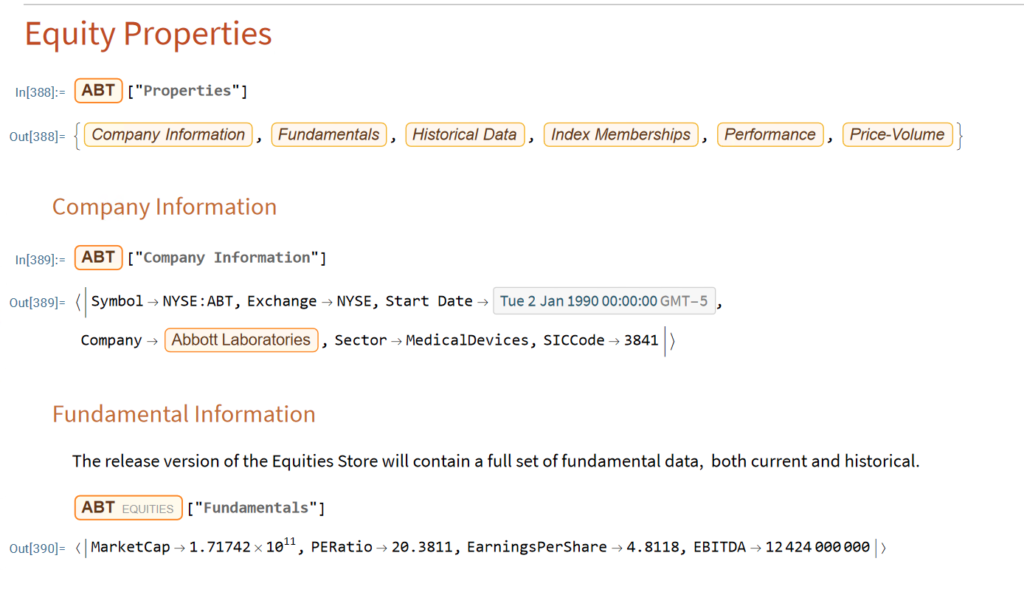
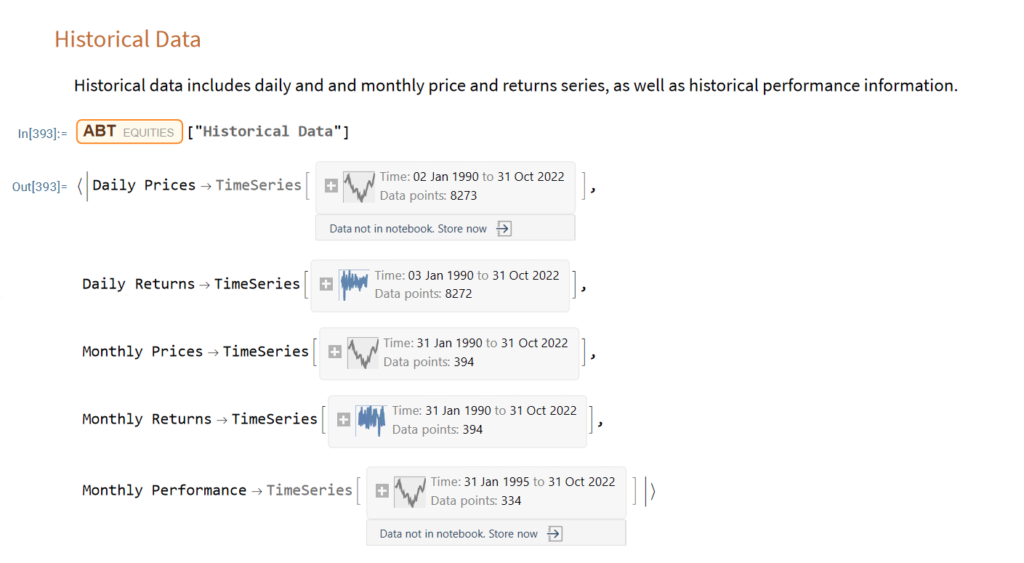
The Wolfram Language stands out in providing an “integrated knowledge base” that spans from sophisticated algorithms to real-world data across domains. This includes vast curated datasets on topics from architecture to chemistry to finance that can readily feed models and analyses without additional wrangling.

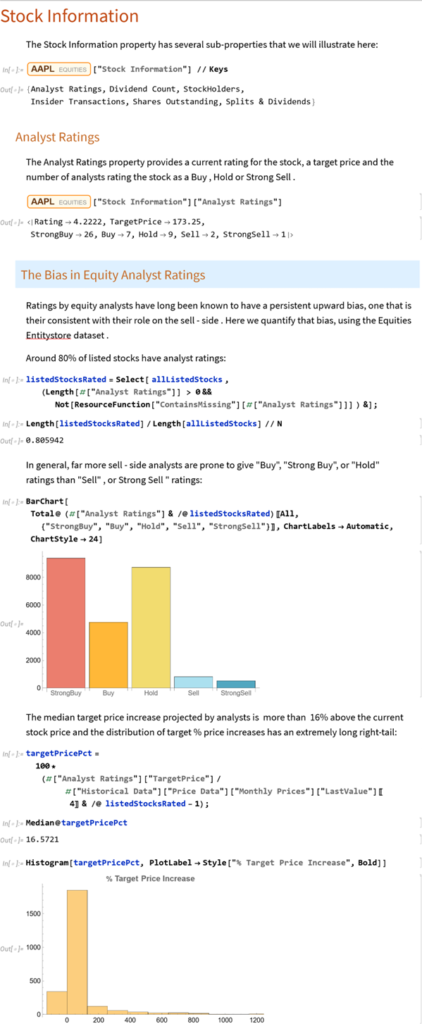
Additionally, the entity store concept allows users to author their own object-based, customizable data repositories. Python’s classes are focused on methods rather than data and while Python offers strong libraries for storing and accessing data, Wolfram facilitates more zero-friction application of real-world knowledge and entity-oriented data storage out-of-the-box. For minimizing time manipulating data or searching for reference algorithms before modeling, Wolfram Language excels.

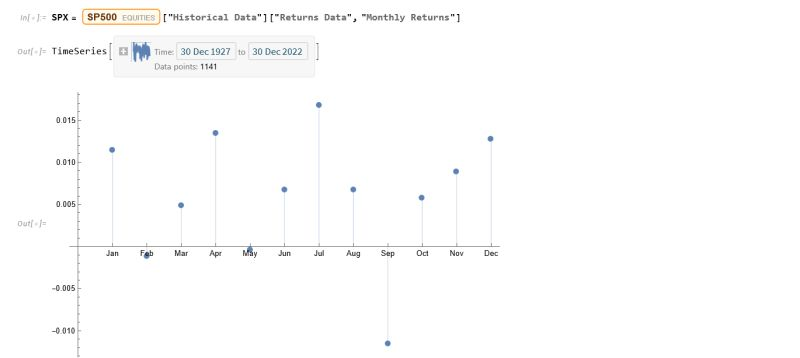
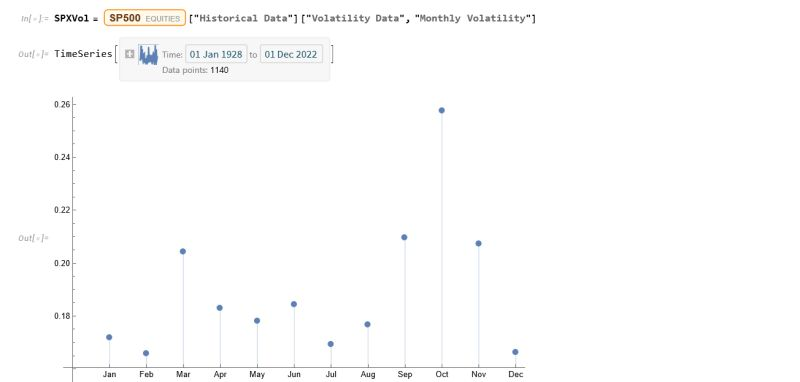
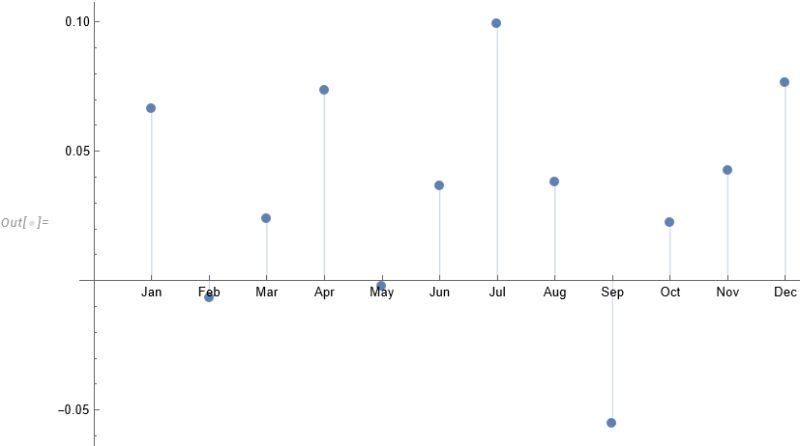
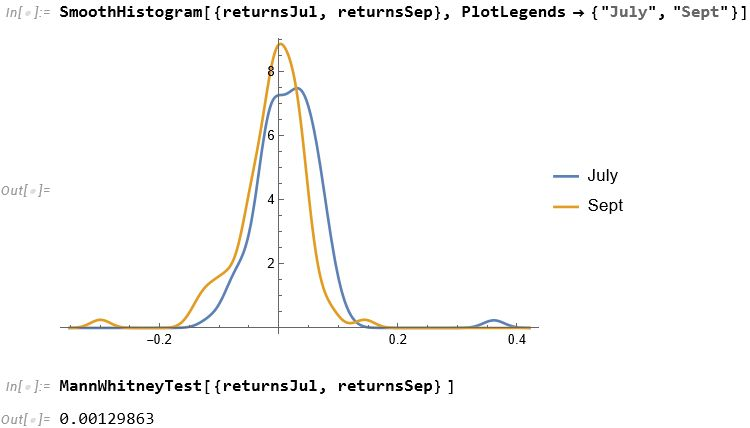
The entity store in particular enables a very natural object/entity-based programming style that can integrate smoothly with Wolfram’s class system and its underlying symbolic capabilities. This unique data representation system differentiation is a key strength (for example, see the Equities Entity Store).

Interactivity and Prototyping

The Wolfram Language excels in hands-on analysis and rapid iteration thanks to its line-by-line execution and built-in Manipulate/Animate functions for customizable graphics, animations and interactive simulations. Python does allow some interactivity in Jupyter notebooks, but does not match Wolfram’s capabilities for creating interactive visualizations on-the-fly. This makes Wolfram Language uniquely well-suited for highly iterative, prototyping tasks that involve visual output. If ease of exploration and fluid development is a priority, the Wolfram Language has clear strengths.

Seamless Parallelization

The Wolfram Language has seamless built-in parallelization capabilities that allow code to efficiently utilize multi-core systems without the developer needing to directly manage threads or processes. Python can achieve parallelism through libraries, but the developer bears responsibility for managing dependencies and avoiding conflicts. Similarly, the Wolfram Language directly interfaces with Nvidia GPUs out-of-the-box for high performance numerical code with minimal extra effort. Thus, for users focused on computational speedup, Wolfram simplifies parallelization and GPU integration in very useful ways.

Python libraries like TensorFlow and PyTorch do hide GPU complexities well for deep learning. But in general, achieving parallel execution in Python places a greater burden on the developer. Wolfram’s approach dramatically lowers the barriers to leveraging multiple cores and GPU power for everyday computations.

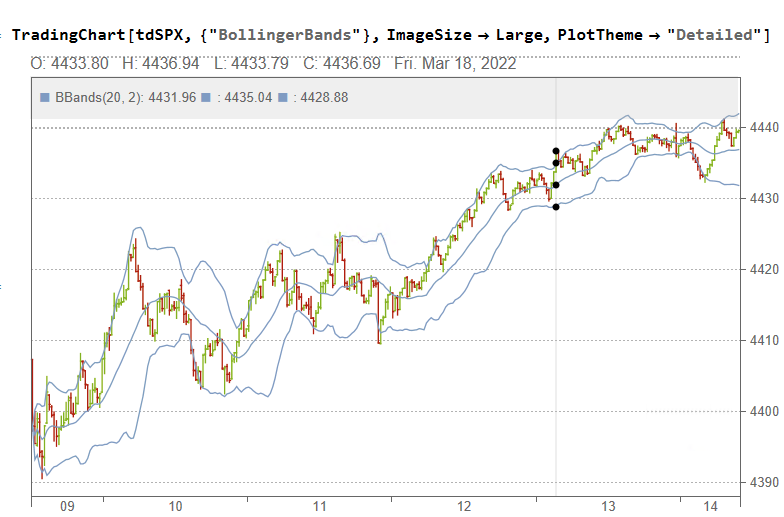
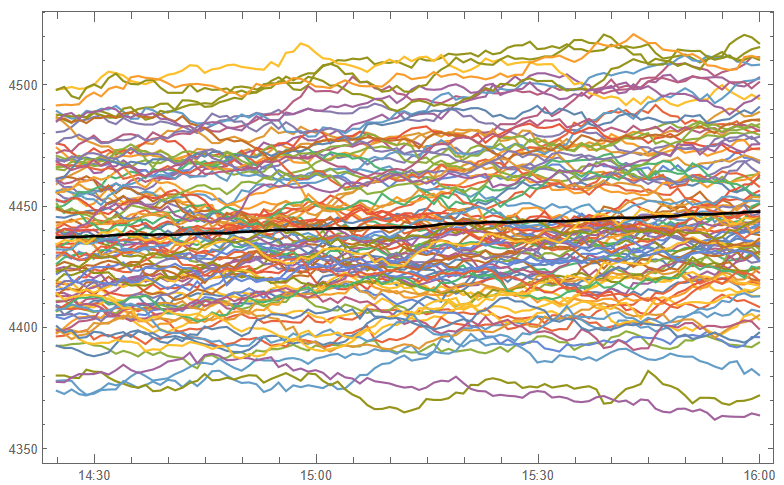
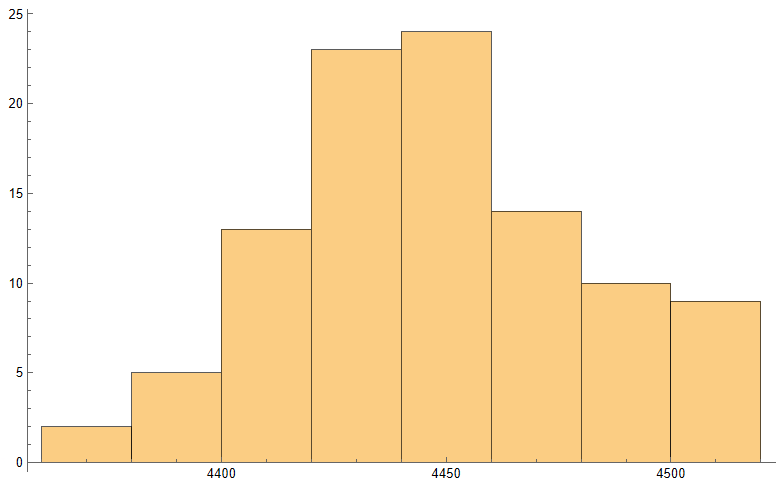
Sophisticated Visualization

Creating publication-quality, customized visualizations requires just lines of code in the Wolfram Language, thanks to the built-in graphics capabilities. While Python offers powerful visualization through add-on libraries like Matplotlib, Seaborn, Bokeh, and Plotly, Wolfram’s out-of-the-box solutions may provide greater ease of use. However, from low-level control to interactive web plots, Python’s visualization options are quite extensive despite requiring more setup. Ultimately, for rapid high-level plotting, Wolfram Language has advantageous default capabilities. But Python gives more flexibility and customization options through its ecosystem of graphic libraries.

In summary, while Python offers flexibility and a large user base – advantages in its own right – the Wolfram Language dramatically reduces lines of code and development time. By curating real-world data, algorithms, and visualization in one coherent language and platform, it streamlines and accelerates quantitative work for scientists, analysts, economists and more.

If you do significant data analysis or modeling, I encourage you to try the Wolfram Language and see the difference yourself. It’s been a gamechanger for my productivity.

Posted on

Seasonality in Equity Returns

To amplify Valérie Noël‘s post a little, we can use the Equities Entity Store (https://lnkd.in/epg-5wwM) to extract returns for the S&P500 index for (almost) the last century and compute the average return by month, as follows.

July is shown to be (by far) the most positive month for the index, with an average return of +1.67%, in stark contrast to the month of Sept. in which the index has experienced an average negative return of -1.15%.

Continuing the analysis a little further, we can again use the the Equities Entity Store (https://lnkd.in/epg-5wwM) to extract estimated average volatility for the S&P500 by calendar month since 1927:

As you can see, July is not only the month with highest average monthly return, but also has amongst the lowest levels of volatility, on average.

Consequently, risk-adjusted average rates of return in July far exceed other months of the year.

Conclusion: bears certainly have a case that the market is over-stretched here, but I would urge caution: hold off until end Q3 before shorting this market in significant size.

For those market analysts who prefer a little more analytical meat, we can compare the median returns for the #S&P500 Index for the months of July and September using the nonparametric MannWhitney test.

This indicates that there is only a 0.13% probability that the series of returns for the two months are generated from distributions with the same median.

Conclusion: Index performance in July really is much better than in September.

For more analysis along these lines, see my recent book, Equity Analytics:

Posted on

Equity Analytics in the Equities Data Store

Equities Entity Store  – A Brief Review

The Equities Entity Store applies the object-oriented concept of Entity Stores in the Wolfram Language to create a collection of equity objects, both stocks and stock indices, containing current and historical fundamental, technical and performance-related data. Also included in the release version of the product will be a collection of utility functions (a.k.a. “Methods”) that will facilitate equity analysis,  the formation and evaluation of equity portfolios and the development and back-testing of equities strategies, including cross-sectional strategies.

In the pre-release version of the store there are just over 1,000 equities, but this will rise to over 2,000 in the first release, as delisted securities are added to the store. This is important in order to eliminate survivor bias from the data set.

First Release of the Equities Entity Store – January 2023

The first release of the equities entity store product will contain around 2,000-2,500 equities, including at least 1,000 active stocks listed on the NYSE and NASDAQ exchanges and a further 1,000-1,500 delisted securities. All of the above information will be available for each equity and, in addition, the historical data will include quarterly fundamental data.

The other major component of the store will be analytics tools, including single-stock analytics functions such as those illustrated here. More important, however, is that the store will contain advanced analytics tools designed to assist the analyst in the construction of optimized equity portfolios and in the development and backtesting of long and long/short equity strategies.

Readers wishing to receive more information should contact me at algosciences (at) gmail.com

Posted on

Intraday Stock Index Forecasting

In a previous post I discussed modelling stock prices processes as Geometric brownian Motion processes:

Understanding Stock Price Range Forecasts

To recap briefly, we assume a process of the form:

Where S0 is the initial stock price at time t = 0.

The mean of such a process is:

and standard deviation:

In the post I showed how to estimate such a process with daily stock prices, using these to provide a forecast range of prices over a one-month horizon. This is potentially useful, for example, in choosing which strikes to select in an option hedge.

Of course, there is nothing to prevent you from using the same technique over different timescales. Here I use the MATH-TWS package to connect Mathematica to the IB TWS platform via the C++ api, to extract intraday prices for the S&P 500 Index at 1-minute intervals. These are used to estimate a short-term GBM process, which provides forecasts of the mean and variance of the index at the 4 PM close.

We capture the data using:

then create a time series of the intraday prices and plot them:

If we want something a little fancier we can create a trading chart, including technical indicators of our choice, for instance:

The charts can be updated in real time from IB, using MATHTWS.

From there we estimate a GBM process using 1-minute close prices:

and then simulate a number of price paths towards the 4 PM close (the mean price path is shown in black):

This indicates that the expected value of the SPX index at the close will be around 4450, which we could estimate directly from:

Where u is the estimated drift of the GBM process.

Similarly we can look at the projected terminal distribution of the index at 4pm to get a sense of the likely range of closing prices, which may assist a decision to open or close certain option (hedge) positions:

Of course, all this is predicated on the underlying process continuing on its current trajectory, with drift and standard deviation close to those seen in the process in the preceding time interval. But trends change, as do volatilities, which means that our forecasts may be inaccurate. Furthermore, the drift in asset processes tends to be dominated by volatility, especially at short time horizons.

So the best way to think of this is as a conditional expectation, i.e. “If the stock price continues on its current trajectory, then our expectation is that the closing price will be in the following range…”.

For more on MATH-TWS see:

MATH-TWS: Connecting Wolfram Mathematica to IB TWS

Posted on

DataScience| Handling Big Data

Handling Large Files in CSV format with NumPy and Pandas

One of the major challenges that users face when trying to do data science is how to handle big data. Leaving aside the important topic of database connectivity/functionality and the handling of data too large to fit in memory, my concern here is with the issue of how to handle large data files, which are often in csv format, but which are not too large to fit into available memory.

It is well known that, due to their generality, Mathematica’s Import and Export functions are horribly slow when handling large csv files. For example, writing out a list of 10 million 64-bit reals takes almost 5 minutes:

No alt text provided for this image

and reading is also unacceptably slow:

No alt text provided for this image

Performance results like these create the impression that Mathematica is suitable for handling only “toy” problems, rather than the kind of large and complex data challenges faced by data scientists in the real world.

Sure, you can speed this up with ReadLine, but not by much, after doing all the string processing. And while the mx binary file format speeds up data handling enormously, it doesn’t address the issue of how to get the data into the requisite file format, other than via the WL DumpSave function – in other words, the data already has to be in a Mathematica notebook in order to write an mx file.

With purely numerical data once way to address this by using non-proprietary binary file formats. For example, in Python we create a NumPy array and use the tofile() method to output the data in real64 binary format, in less then 2 seconds:

No alt text provided for this image

Then in Mathematica the read process is equally fast when processing a file of numerical data in binary format, around 50x faster than the time taken to process the same file in csv format:

No alt text provided for this image

The procedure is just as fast in the reverse direction, with binary data exports from Mathematica taking a fraction of the time required to process the same data in csv format (around 200x faster!):

No alt text provided for this image

And the data is extremely fast read back in Python using the numpy fromfile method:

No alt text provided for this image

This procedure is robust enough to accommodate missing data. For instance, let’s replace some of the values in our data array with np.nan values and export the file once again in binary format:

No alt text provided for this image

Reading the binary file into Mathematica, we find no reduction in speed, as the np.nan values are stored as decimals, which are replaced by the value Indeterminate in the imported Mathematica array:

No alt text provided for this image

So, for purely numerical data we have a fast and reliable procedure for transferring data between Python, R and Mathematica using binary format. This means that we can load very large csv files in Python, do some pre-processing in pandas and export the massaged data in binary format for further analysis in Mathematica, if required.

More Complex Data Structures: the HDF5 Format

A major step in the right direction has been achieved through the significant effort that WR has put into implementing the HDF5 binary file format standard in the Wolfram Language. This serves two purposes: firstly, it can speed up the storage and retrieval of large datasets, by orders of magnitudes (depending on the data type); secondly, unlike Wolfram’s proprietary mx file format, HDF5 is an open source format that can store large, complex & hierarchical datasets that are accessible via Python, R and MatLab, as well as other languages/platforms, including Mathematica. So, working with the same dataset as before, but using HDF5 format, we get an speed-up of around 500x on the file write and around 270x on the file read:

No alt text provided for this image

Another major benefit of working in binary format is the enormous saving in disk storage, compared to csv:

No alt text provided for this image

So it becomes feasible to envisage a workflow in which some pre-processing of a very large dataset in csv format takes place initially in e.g. Python Pandas, the results of which are exported to a HDF5 or binary format file for further processing in Mathematica.

This advance does a great deal to address some of the major concerns about using Mathematica for large data science projects. And I am not sure that users are necessarily aware of its significance, given all the hoopla over more glamorous features that tend to get all the attention in new version releases.

Posted on

A Winer Process

No doubt many of you sharp-eyed readers will have spotted a spelling error, thinking I intended to refer to one of these:

Fig 1

 

But, in fact, I really did have in mind something more like this:

 

wine pour

 

We are following an example from the recently published Mathematica Beyond Mathematics by Jose Sanchez Leon, an up-to-date text that describes many of the latest features in Mathematica, illustrated with interesting applications. Sanchez Leon shows how Mathematica’s machine learning capabilities can be applied to the craft of wine-making.

SSALGOTRADING AD

We begin by loading a curated Wolfram dataset comprising measurements of the physical properties and quality of wines:

Fig 2

A Machine Learning Prediction Model for Wine Quality

We’re going to apply Mathematica’s built-in machine learning algorithms to train a predictor of wine quality, using the training dataset. Mathematica determines that the most effective machine learning technique in this case is Random Forest and after a few seconds produces the predictor function:

Fig 3

 

Mathematica automatically selects what it considers to be the best performing model from several available machine learning algorithms:

machine learning methods

Let’s take a look at how well the predictor perform on the test dataset of 1,298 wines:

Fig 4

We can use the predictor function to predict the quality of an unknown wine, based on its physical properties:

Fig 5

Next we create a function to predict the quality of an unknown wine as a function of just two of its characteristics, its pH and alcohol level.  The analysis suggests that the quality of our unknown wine could be improved by increasing both its pH and alcohol content:

Fig 6

Applications and Examples

This simple toy example illustrates how straightforward it is to deploy machine learning techniques in Mathematica.  Machine Learning and Neural Networks became a major focus for Wolfram Research in version 10, and the software’s capabilities have been significantly enhanced in version 11, with several applications such as text and sentiment analysis that have direct relevance to trading system development:

Fig 7

For other detailed examples see:

http://jonathankinlay.com/2016/08/machine-learning-model-spy/

http://jonathankinlay.com/2016/11/trading-market-sentiment/

 

http://jonathankinlay.com/2016/08/dynamic-time-warping/

 

 

 

 

 

Posted on

Conditional Value at Risk Models

One of the most widely used risk measures is the Value-at-Risk, defined as the expected loss on a portfolio at a specified confidence level. In other words, VaR is a percentile of a loss distribution.
But despite its popularity VaR suffers from well-known limitations: its tendency to underestimate the risk in the (left) tail of the loss distribution and its failure to capture the dynamics of correlation between portfolio components or nonlinearities in the risk characteristics of the underlying assets.

SSALGOTRADING AD

One method of seeking to address these shortcomings is discussed in a previous post Copulas in Risk Management. Another approach known as Conditional Value at Risk (CVaR), which seeks to focus on tail risk, is the subject of this post.  We look at how to estimate Conditional Value at Risk in both Gaussian and non-Gaussian frameworks, incorporating loss distributions with heavy tails and show how to apply the concept in the context of nonlinear time series models such as GARCH.

 

Var, CVaR and Heavy Tails