Robustness Archives - QUANTITATIVE RESEARCH AND TRADING

September 29, 2020

Robustness in Quantitative Research and Trading

What is Strategy Robustness? What is its relevance to Quantitative Research and Trading?

One of the most highly desired properties of any financial model or investment strategy, by investors and managers alike, is robustness. I would define robustness as the ability of the strategy to deliver a consistent results across a wide range of market conditions. It, of course, by no means the only desirable property – investing in Treasury bills is also a pretty robust strategy, although the returns are unlikely to set an investor’s pulse racing – but it does ensure that the investor, or manager, is unlikely to be on the receiving end of an ugly surprise when market conditions adjust.

Robustness is not the same thing as low volatility, which also tends to be a characteristic highly prized by many investors. A strategy may operate consistently, with low volatility in certain market conditions, but behave very differently in other. For instance, a delta-hedged short-volatility book containing exotic derivative positions. The point is that empirical researchers do not know the true data-generating process for the markets they are modeling. When specifying an empirical model they need to make arbitrary assumptions. An example is the common assumption that assets returns follow a Gaussian distribution. In fact, the empirical distribution of the great majority of asset process exhibit the characteristic of “fat tails”, which can result from the interplay between multiple market states with random transitions. See this post for details:

http://jonathankinlay.com/2014/05/a-quantitative-analysis-of-stationarity-and-fat-tails/

In statistical arbitrage, for example, quantitative researchers often make use of cointegration models to build pairs trading strategies. However the testing procedures used in current practice are not sufficient powerful to distinguish between cointegrated processes and those whose evolution just happens to correlate temporarily, resulting in the frequent breakdown in cointegrating relationships. For instance, see this post:

http://jonathankinlay.com/2017/06/statistical-arbitrage-breaks/

Modeling Assumptions are Often Wrong – and We Know It

We are, of course, not the first to suggest that empirical models are misspecified:

“All models are wrong, but some are useful” (Box 1976, Box and Draper 1987).

Martin Feldstein (1982: 829): “In practice all econometric specifications are necessarily false models.”

Luke Keele (2008: 1): “Statistical models are always simplifications, and even the most complicated model will be a pale imitation of reality.”

Peter Kennedy (2008: 71): “It is now generally acknowledged that econometric models are false and there is no hope, or pretense, that through them truth will be found.”

During the crash of 2008 quantitative Analysts and risk managers found out the hard way that the assumptions underpinning the copula models used to price and hedge credit derivative products were highly sensitive to market conditions. In other words, they were not robust. See this post for more on the application of copula theory in risk management:

http://jonathankinlay.com/2017/01/copulas-risk-management/

Robustness Testing in Quantitative Research and Trading

We interpret model misspecification as model uncertainty. Robustness tests analyze model uncertainty by comparing a baseline model to plausible alternative model specifications. Rather than trying to specify models correctly (an impossible task given causal complexity), researchers should test whether the results obtained by their baseline model, which is their best attempt of optimizing the specification of their empirical model, hold when they systematically replace the baseline model specification with plausible alternatives. This is the practice of robustness testing.

Robustness testing analyzes the uncertainty of models and tests whether estimated effects of interest are sensitive to changes in model specifications. The uncertainty about the baseline model’s estimated effect size shrinks if the robustness test model finds the same or similar point estimate with smaller standard errors, though with multiple robustness tests the uncertainty likely increases. The uncertainty about the baseline model’s estimated effect size increases of the robustness test model obtains different point estimates and/or gets larger standard errors. Either way, robustness tests can increase the validity of inferences.

Robustness testing replaces the scientific crowd by a systematic evaluation of model alternatives.

Robustness in Quantitative Research

In the literature, robustness has been defined in different ways:

as same sign and significance (Leamer)
as weighted average effect (Bayesian and Frequentist Model Averaging)
as effect stability We define robustness as effect stability.

Parameter Stability and Properties of Robustness

Robustness is the share of the probability density distribution of the baseline model that falls within the 95-percent confidence interval of the baseline model. In formulaeic terms:

Robustness is left-–right symmetric: identical positive and negative deviations of the robustness test compared to the baseline model give the same degree of robustness.
If the standard error of the robustness test is smaller than the one from the baseline model, ρ converges to 1 as long as the difference in point estimates is negligible.
For any given standard error of the robustness test, ρ is always and unambiguously smaller the larger the difference in point estimates.
Differences in point estimates have a strong influence on ρ if the standard error of the robustness test is small but a small influence if the standard errors are large.

Robustness Testing in Four Steps

Define the subjectively optimal specification for the data-generating process at hand. Call this model the baseline model.
Identify assumptions made in the specification of the baseline model which are potentially arbitrary and that could be replaced with alternative plausible assumptions.
Develop models that change one of the baseline model’s assumptions at a time. These alternatives are called robustness test models.
Compare the estimated effects of each robustness test model to the baseline model and compute the estimated degree of robustness.

Model Variation Tests

Model variation tests change one or sometimes more model specification assumptions and replace with an alternative assumption, such as:

change in set of regressors
change in functional form
change in operationalization
change in sample (adding or subtracting cases)

Example: Functional Form Test

The functional form test examines the baseline model’s functional form assumption against a higher-order polynomial model. The two models should be nested to allow identical functional forms. As an example, we analyze the ‘environmental Kuznets curve’ prediction, which suggests the existence of an inverse u-shaped relation between per capita income and emissions.

Note: grey-shaded area represents confidence interval of baseline model

Another example of functional form testing is given in this review of Yield Curve Models:

http://jonathankinlay.com/2018/08/modeling-the-yield-curve/

Random Permutation Tests

Random permutation tests change specification assumptions repeatedly. Usually, researchers specify a model space and randomly and repeatedly select model from this model space. Examples:

sensitivity tests (Leamer 1978)
artificial measurement error (Plümper and Neumayer 2009)
sample split – attribute aggregation (Traunmüller and Plümper 2017)
multiple imputation (King et al. 2001)

We use Monte Carlo simulation to test the sensitivity of the performance of our Quantitative Equity strategy to changes in the price generation process and also in model parameters:

http://jonathankinlay.com/2017/04/new-longshort-equity/

Structured Permutation Tests

Structured permutation tests change a model assumption within a model space in a systematic way. Changes in the assumption are based on a rule, rather than random. Possibilities here include:

sensitivity tests (Levine and Renelt)
jackknife test
partial demeaning test

Example: Jackknife Robustness Test

The jackknife robustness test is a structured permutation test that systematically excludes one or more observations from the estimation at a time until all observations have been excluded once. With a ‘group-wise jackknife’ robustness test, researchers systematically drop a set of cases that group together by satisfying a certain criterion – for example, countries within a certain per capita income range or all countries on a certain continent. In the example, we analyse the effect of earthquake propensity on quake mortality for countries with democratic governments, excluding one country at a time. We display the results using per capita income as information on the x-axes.

Upper and lower bound mark the confidence interval of the baseline model.

Robustness Limit Tests

Robustness limit tests provide a way of analyzing structured permutation tests. These tests ask how much a model specification has to change to render the effect of interest non-robust. Some examples of robustness limit testing approaches:

unobserved omitted variables (Rosenbaum 1991)
measurement error
under- and overrepresentation
omitted variable correlation

For an example of limit testing, see this post on a review of the Lognormal Mixture Model:

http://jonathankinlay.com/2018/08/the-lognormal-mixture-variance-model/

Summary on Robustness Testing

Robustness tests have become an integral part of research methodology. Robustness tests allow to study the influence of arbitrary specification assumptions on estimates. They can identify uncertainties that otherwise slip the attention of empirical researchers. Robustness tests offer the currently most promising answer to model uncertainty.

September 21, 2018

Building Systematic Strategies – A New Approach

Anyone active in the quantitative space will tell you that it has become a great deal more competitive in recent years. Many quantitative trades and strategies are a lot more crowded than they used to be and returns from existing strategies are on the decline.

THE CHALLENGE

Meanwhile, costs have been steadily rising, as the technology arms race has accelerated, with more money being spent on hardware, communications and software than ever before. As lead times to develop new strategies have risen, the cost of acquiring and maintaining expensive development resources have spiraled upwards. It is getting harder to find new, profitable strategies, due in part to the over-grazing of existing methodologies and data sets (like the E-Mini futures, for example). There has, too, been a change in the direction of quantitative research in recent years. Where once it was simply a matter of acquiring the fastest pipe to as many relevant locations as possible, the marginal benefit of each extra $ spent on infrastructure has since fallen rapidly. New strategy research and development is now more model-driven than technology driven.

THE OPPORTUNITY

What is needed at this point is a new approach: one that accelerates the process of identifying new alpha signals, prototyping and testing new strategies and bringing them into production, leveraging existing battle-tested technologies and trading platforms.

GENETIC PROGRAMMING

Genetic programming, which has been around since the 1990’s when its use was pioneered in proteomics, enjoys significant advantages over traditional research and development methodologies.

GP is an evolutionary-based algorithmic methodology in which a system is given a set of simple rules, some data, and a fitness function that produces desired outcomes from combining the rules and applying them to the data. The idea is that, by testing large numbers of possible combinations of rules, typically in the millions, and allowing the most successful rules to propagate, eventually we will arrive at a strategy solution that offers the required characteristics.

ADVANTAGES OF GENETIC PROGRAMMING

The potential benefits of the GP approach are considerable: not only are strategies developed much more quickly and cost effectively (the price of some software and a single CPU vs. a small army of developers), the process is much more flexible. The inflexibility of the traditional approach to R&D is one of its principle shortcomings. The researcher produces a piece of research that is subsequently passed on to the development team. Developers are usually extremely rigid in their approach: when asked to deliver X, they will deliver X, not some variation on X. Unfortunately research is not an exact science: what looks good in a back-test environment may not pass muster when implemented in live trading. So researchers need to “iterate around” the idea, trying different combinations of entry and exit logic, for example, until they find a variant that works. Developers are lousy at this; GP systems excel at it.

CHALLENGES FOR THE GENETIC PROGRAMMING APPROACH

So enticing are the potential benefits of GP that it begs the question as to why the approach hasn’t been adopted more widely. One reason is the strong preference amongst researchers for an understandable – and testable – investment thesis. Researchers – and, more importantly, investors – are much more comfortable if they can articulate the premise behind a strategy. Even if a trade turns out to be a loser, we are generally more comfortable buying a stock on the supposition of, say, a positive outcome of a pending drug trial, than we are if required to trust the judgment of a black box, whose criteria are inherently unobservable.

Added to this, the GP approach suffers from three key drawbacks: data sufficiency, data mining and over-fitting. These are so well known that they hardly require further rehearsal. There have been many adverse outcomes resulting from poorly designed mechanical systems curve fitted to the data. Anyone who was active in the space in the 1990s will recall the hype over neural networks and the over-exaggerated claims made for their efficacy in trading system design. Genetic Programming, a far more general and powerful concept, suffered unfairly from the ensuing adverse publicity, although it does face many of the same challenges.

A NEW APPROACH

I began working in the field of genetic programming in the 1990’s, with my former colleague Haftan Eckholdt, at that time head of neuroscience at Yeshiva University, and we founded a hedge fund, Proteom Capital, based on that approach (large due to Haftan’s research). I and my colleagues at Systematic Strategies have continued to work on GP related ideas over the last twenty years, and during that period we have developed a methodology that address the weaknesses that have held back genetic programming from widespread adoption.

Firstly, we have evolved methods for transforming original data series that enables us to avoid over-using the same old data-sets and, more importantly, allows new patterns to be revealed in the underlying market structure. This effectively eliminates the data mining bias that has plagued the GP approach. At the same time, because our process produces a stronger signal relative to the background noise, we consume far less data – typically no more than a couple of years worth.

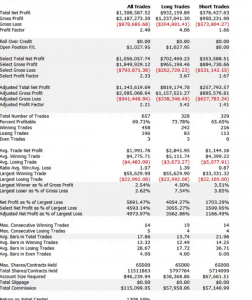
Secondly, we have found we can enhance the robustness of prototype strategies by using double-blind testing: i.e. data sets on which the performance of the model remains unknown to the machine, or the researcher, prior to the final model selection.

Finally, we are able to test not only the alpha signal, but also multiple variations of the trade expression, including different types of entry and exit logic, as well as profit targets and stop loss constraints.

OUTCOMES: ROBUST, PROFITABLE STRATEGIES

Taken together, these measures enable our GP system to produce strategies that not only have very high performance characteristics, but are also extremely robust. So, for example, having constructed a model using data only from the continuing bull market in equities in 2012 and 2013, the system is nonetheless capable of producing strategies that perform extremely well when tested out of sample over the highly volatility bear market conditions of 2008/09.

So stable are the results produced by many of the strategies, and so well risk-controlled, that it is possible to deploy leveraged money-managed techniques, such as Vince’s fixed fractional approach. Money management schemes take advantage of the high level of consistency in performance to increase the capital allocation to the strategy in a way that boosts returns without incurring a high risk of catastrophic loss. You can judge the benefits of applying these kinds of techniques in some of the strategies we have developed in equity, fixed income, commodity and energy futures which are described below.

CONCLUSION

After 20-30 years of incubation, the Genetic Programming approach to strategy research and development has come of age. It is now entirely feasible to develop trading systems that far outperform the overwhelming majority of strategies produced by human researchers, in a fraction of the time and for a fraction of the cost.

SAMPLE GP SYSTEMS

September 17, 2018

Creating Robust, High-Performance Stock Portfolios

Summary

In this article, I am going to look at how stock portfolios should be constructed that best meet investment objectives.

The theoretical and practical difficulties of the widely adopted Modern Portfolio Theory approach limits its usefulness as a tool for portfolio construction.

MPT portfolios typically produce disappointing out-of-sample results, and will often underperform a naïve, equally-weighted stock portfolio.

The article introduces the concept of robust portfolio construction, which leads to portfolios that have more stable performance characteristics, including during periods of high volatility or market corrections.

The benefits of this approach include risk-adjusted returns that substantially exceed those of traditional portfolios, together with much lower drawdowns and correlations.

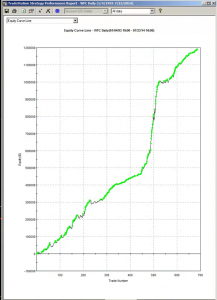
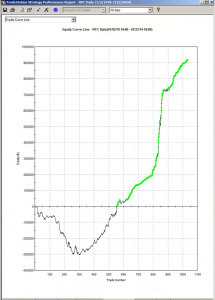
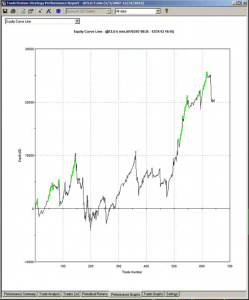
Market Timing

In an earlier article, I discussed how investors can enhance returns through the strategic use of market timing techniques to step out of the market during difficult conditions.

To emphasize the impact of market timing on investment returns, I have summarized in the chart below how a $1,000 investment would have grown over the 25-year period from July 1990 to June 2014. In the baseline scenario, we assume that the investment is made in a fund that tracks the S&P 500 Index and held for the full term. In the second scenario, we look at the outcome if the investor had stepped out of the market during the market downturns from March 2000 to Feb 2003 and from Jan 2007 to Feb 2009.

Fig. 1: Value of $1,000 Jul 1990-Jun 2014 – S&P 500 Index with and without Market Timing

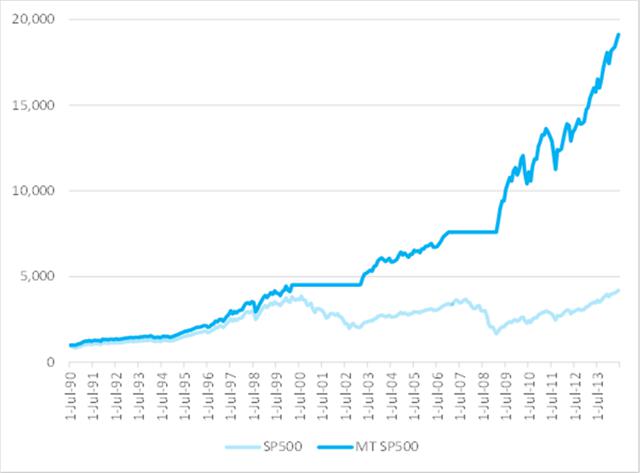
Source: Yahoo Finance, 2014

After 25 years, the investment under the second scenario would have been worth approximately 5x as much as in the baseline scenario. Of course, perfect market timing is unlikely to be achievable. The best an investor can do is employ some kind of market timing indicator, such as the CBOE VIX index, as described in the previous article.

Equity Long Short

For those who mistrust the concept of market timing or who wish to remain invested in the market over the long term regardless of short-term market conditions, an alternative exists that bears consideration.

The equity long/short strategy, in which the investor buys certain stocks while shorting others, is a concept that reputedly originated with Alfred Jones in the 1940s. A long/short equity portfolio seeks to reduce overall market exposure, while profiting from stock gains in the long positions and price declines in the short positions. The idea is that the investor’s equity investments in the long positions are hedged to some degree against a general market decline by the offsetting short positions, from which the concept of a hedge fund is derived.

There are many variations on the long/short theme. Where the long and short positions are individually matched, the strategy is referred to as pairs trading. When the portfolio composition is structured in a way that the overall market exposure on the short side equates to that of the long side, leaving zero net market exposure, the strategy is typically referred to as market-neutral. Variations include dollar-neutral, where the dollar value of aggregate long and short positions is equalized, and beta-neutral, where the portfolio is structured in a way to yield a net zero overall market beta. But in the great majority of cases, such as, for example, in 130/30 strategies, there is a residual net long exposure to the market. Consequently, for the most part, long/short strategies are correlated with the overall market, but they will tend to outperform long-only strategies during market declines, while underperforming during strong market rallies.

Modern Portfolio Theory

Theories abound as to the best way to construct equity portfolios. The most commonly used approach is mean-variance optimization, a concept developed in the 1950s by Harry Markovitz (other more modern approaches include, for example, factor models or CVAR – conditional value at risk).

If we plot the risk and expected return of the assets under consideration, in what is referred to as the investment opportunity set, we see a characteristic “bullet” shape, the upper edge of which is called the efficient frontier (See Fig. 2). Assets on the efficient frontier produce the highest level of expected return for a given level of risk. Equivalently, a portfolio lying on the efficient frontier represents the combination offering the best possible expected return for a given risk level. It transpires that for efficient portfolios, the weights to be assigned to individual assets depend only on the volatilities of the individual assets and the correlation between them, and can be determined by simple linear programming. The inclusion of a riskless asset (such as US T-bills) allows us to construct the Capital Market Line, shown in the figure, which is tangent to the efficient frontier at the portfolio with the highest Sharpe Ratio, which is consequently referred to as the Tangency or Optimal Portfolio.

Fig. 2: Investment Opportunity Set and Efficient Frontier

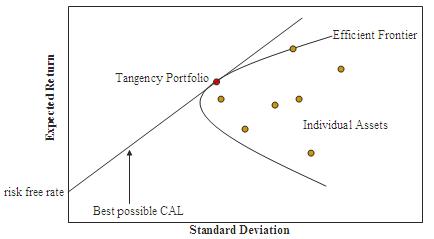
Source: Wikipedia

Paradise Lost

Elegant as it is, MPT is open to challenge as a suitable basis for constructing investment portfolios. The Sharpe Ratio is often an inadequate representation of the investor’s utility function – for example, a strategy may have a high Sharpe Ratio but suffer from large drawdowns, behavior unlikely to be appealing to many investors. Of greater concern is the assumption of constant correlation between the assets in the investment universe. In fact, expected returns, volatilities and correlations fluctuate all the time, inducing changes in the shape of the efficient frontier and the composition of the optimal portfolio, which may be substantial. Not only is the composition of the optimal portfolio unstable, during times of financial crisis, all assets tend to become positively correlated and move down together. The supposed diversification benefit of MPT breaks down when it is needed the most.

I want to spend a little time on these critical issues before introducing a new methodology for portfolio construction. I will illustrate the procedure using a limited investment universe consisting of the dozen stocks listed below. This is, of course, a much more restricted universe than would typically apply in practice, but it does provide a span of different sectors and industries sufficient for our purpose.

Adobe Systems Inc. (NASDAQ:ADBE)

E. I. du Pont de Nemours and Company (NYSE:DD)

The Dow Chemical Company (NYSE:DOW)

Emerson Electric Co. (NYSE:EMR)

Honeywell International Inc. (NYSE:HON)

International Business Machines Corporation (NYSE:IBM)

McDonald’s Corp. (NYSE:MCD)

Oracle Corporation (NYSE:ORCL)

The Procter & Gamble Company (NYSE:PG)

Texas Instruments Inc. (NASDAQ:TXN)

Wells Fargo & Company (NYSE:WFC)

Williams Companies, Inc. (NYSE:WMB)

If we follow the procedure outlined in the preceding section, we arrive at the following depiction of the investment opportunity set and efficient frontier. Note that in the following, the S&P 500 index is used as a proxy for the market portfolio, while the equal portfolio designates a portfolio comprising identical dollar amounts invested in each stock.

Fig. 3: Investment Opportunity Set and Efficient Frontiers for the 12-Stock Portfolio

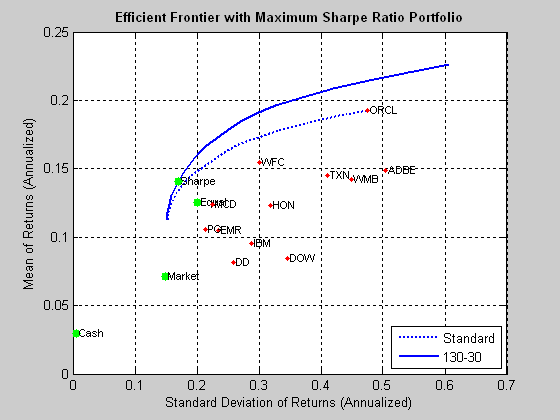
Source: MathWorks Inc.

As you can see, we have derived not one, but two, efficient frontiers. The first is the frontier for standard portfolios that are constrained to be long-only and without use of leverage. The second represents the frontier for 130/30 long-short portfolios, in which we permit leverage of 30%, so that long positions are overweight by a total of 30%, offset by a 30% short allocation. It turns out that in either case, the optimal portfolio yields an average annual return of around 13%, with annual volatility of around 17%, producing a Sharpe ratio of 0.75.

So far so good, but here, of course, we are estimating the optimal portfolio using the entire data set. In practice, we will need to estimate the optimal portfolio with available historical data and rebalance on a regular basis over time. Let’s assume that, starting in July 1995 and rolling forward month by month, we use the latest 60 months of available data to construct the efficient frontier and optimal portfolio.

Fig. 4 below illustrates the enormous variation in the shape of the efficient frontier over time, and in the risk/return profile of the optimal long-only portfolio, shown as the white line traversing the frontier surface.

Fig. 4: Time Evolution of the Efficient Frontier and Optimal Portfolio

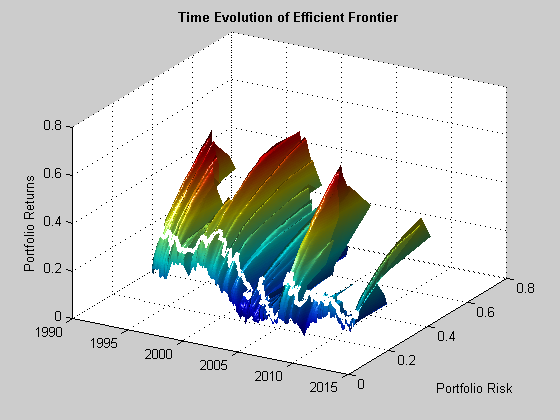
Source: MathWorks Inc.

We see in Fig. 5 that the outcome of using the MPT approach is hardly very encouraging: the optimal long-only portfolio underperforms the market both in aggregate, over the entire back-test period, and consistently during the period from 2000-2011. The results for a 130/30 portfolio (not shown) are hardly an improvement, as the use of leverage, if anything, has a tendency to exacerbate portfolio turnover and other undesirable performance characteristics.

Fig. 5: Value of $1,000: Optimal Portfolio vs. S&P 500 Index, Jul 1995-Jun 2014

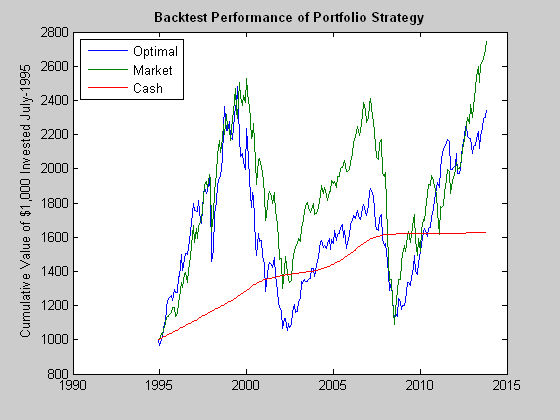
Source: MathWorks Inc.

Part of the reason for the poor performance of the optimal portfolio lies with the assumption of constant correlation. In fact, as illustrated in Fig 6, the average correlation between the monthly returns in the twelve stocks in our universe has fluctuated very substantially over the last twenty years, ranging from a low of just over 20% to a high in excess of 50%, with an annual volatility of 38%. Clearly, the assumption of constant correlation is unsafe.

Fig. 6: Average Correlation, Jul 1995-Jun 2014

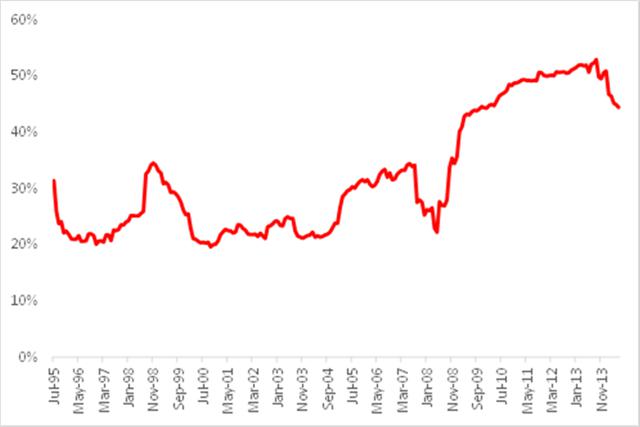
Source: Yahoo Finance, 2014

To add to the difficulties, researchers have found that the out of sample performance of the naïve portfolio, in which equal dollar value is invested in each stock, is typically no worse than that of portfolios constructed using techniques such as mean-variance optimization or factor models¹. Due to the difficulty of accurately estimating asset correlations, it would require an estimation window of 3,000 months of historical data for a portfolio of only 25 assets to produce a mean-variance strategy that would outperform an equally-weighted portfolio!

Without piling on the agony with additional concerns about the MPT methodology, such as the assumption of Normality in asset returns, it is already clear that there are significant shortcomings to the approach.

Robust Portfolios

Many attempts have been made by its supporters to address the practical limitations of MPT, while other researchers have focused attention on alternative methodologies. In practice, however, it remains a challenge for any of the common techniques in use today to produce portfolios that will consistently outperform a naïve, equally-weighted portfolio. The approach discussed here represents a radical departure from standard methods, both in its objectives and in its methodology. I will discuss the general procedure without getting into all of the details, some of which are proprietary.

Let us revert for a moment to the initial discussion of market timing at the start of this article. We showed that if only we could time the market and step aside during major market declines, the outcome for the market portfolio would be a five-fold improvement in performance over the period from Aug 1990 to Jun 2014. In one sense, it would not take “much” to produce a substantial uplift in performance: what is needed is simply the ability to avoid the most extreme market drawdowns. We can identify this as a feature of what might be described as a “robust” portfolio, i.e. one with a limited tendency to participate in major market corrections. Focusing now on the general concept of “robustness”, what other characteristics might we want our ideal portfolio to have? We might consider, for example, some or all of the following:

Ratio of total returns to max drawdown
Percentage of profitable days
Number of drawdowns and average length of drawdowns
Sortino ratio
Correlation to perfect equity curve
Profit factor (ratio of gross profit to gross loss)
Variability in average correlation

The list is by no means exhaustive or prescriptive. But these factors relate to a common theme, which we may characterize as robustness. A portfolio or strategy constructed with these criteria in mind is likely to have a very different composition and set of performance characteristics when compared to an optimal portfolio in the mean-variance sense. Furthermore, it is by no means the case that the robustness of such a portfolio must come at the expense of lower expected returns. As we have seen, a portfolio which only produces a zero return during major market declines has far higher overall returns than one that is correlated with the market. If the portfolio can be constructed in a way that will tend to produce positive returns during market downturns, so much the better. In other words, what we are describing is a long/short portfolio whose correlation to the market adapts to market conditions, having a tendency to become negative when markets are in decline and positive when they are rising.

The first insight of this approach, then, is that we use different criteria, often multi-dimensional, to define optimality. These criteria have a tendency to produce portfolios that behave robustly, performing well during market declines or periods of high volatility, as well as during market rallies.

The second insight from the robust portfolio approach arises from the observation that, ideally, we would want to see much greater consistency in the correlations between assets in the investment universe than is typically the case for stock portfolios. Now, stock correlations are what they are and fluctuate as they will – there is not much one can do about that, at least directly. One solution might be to include other assets, such as commodities, into the mix, in an attempt to reduce and stabilize average asset correlations. But not only is this often undesirable, it is unnecessary – one can, in fact, reduce average correlation levels, while remaining entirely with the equity universe.

The solution to this apparent paradox is simple, albeit entirely at odds with the MPT approach. Instead of creating our portfolio on the basis of combining a group of stocks in some weighting scheme, we are first going to develop investment strategies for each of the stocks individually, before combining them into a portfolio. The strategies for each stock are designed according to several of the criteria of robustness we identified earlier. When combined together, these individual strategies will merge to become a portfolio, with allocations to each stock, just as in any other weighting scheme. And as with any other portfolio, we can set limits on allocations, turnover, or leverage. In this case, however, the resulting portfolio will, like its constituent strategies, display many of the desired characteristics of robustness.

Let’s take a look at how this works out for our sample universe of twelve stocks. I will begin by focusing on the results from the two critical periods from March 2000 to Feb 2003 and from Jan 2007 to Feb 2009.

Fig. 7: Robust Equity Long/Short vs. S&P 500 index, Mar 2000-Feb 2003

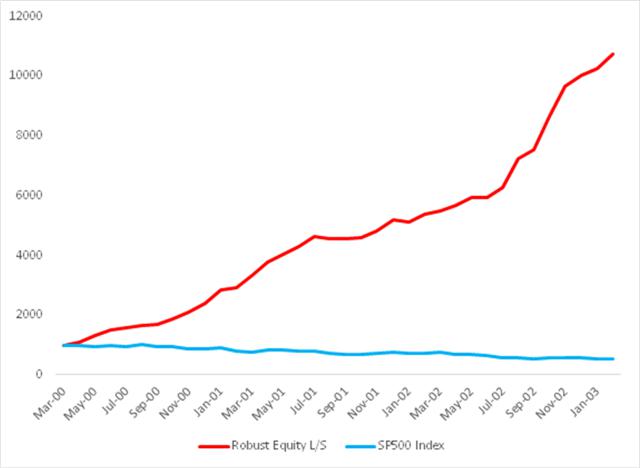
Source: Yahoo Finance, 2014

Fig. 8: Robust Equity Long/Short vs. S&P 500 index, Jan 2007-Feb 2009

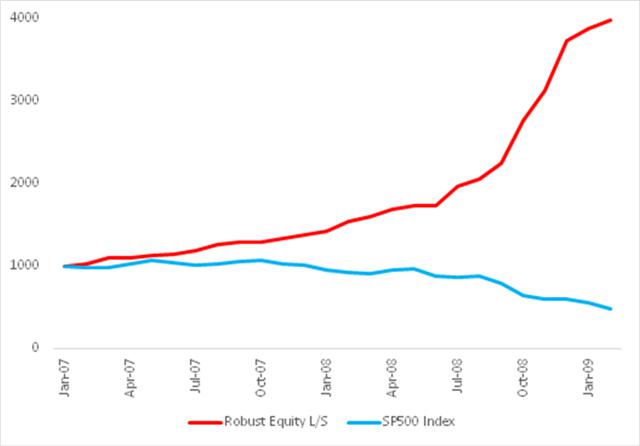
Source: Yahoo Finance, 2014

As might be imagined, given its performance during these critical periods, the overall performance of the robust portfolio dominates the market portfolio over the entire period from 1990:

Fig. 9: Robust Equity Long/Short vs. S&P 500 index, Aug 1990-Jun 2014

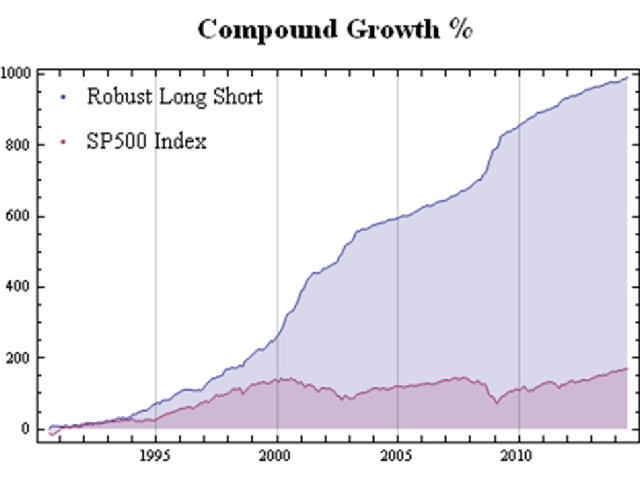
Source: Yahoo Finance, 2014

It is worth pointing out that even during benign market conditions, such as those prevailing from, say, the end of 2012, the robust portfolio outperforms the market portfolio on a risk-adjusted basis: while the returns are comparable for both, around 36% in total, the annual volatility of the robust portfolio is only 4.8%, compared to 8.4% for the S&P 500 index.

A significant benefit to the robust portfolio derives from the much lower and more stable average correlation between its constituent strategies, compared to the average correlation between the individual equities, which we considered before. As can be seen from Fig. 10, average correlation levels remained under 10% for the robust portfolio, compared to around 25% for the mean-variance optimal portfolio until 2008, rising only to a maximum value of around 15% in 2009. Thereafter, average correlation levels have drifted consistently in the downward direction, and are now very close to zero. Overall, average correlations are much more stable for the constituents in the robust portfolio than for those in the traditional portfolio: annual volatility at 12.2% is less than one-third of the annual volatility of the latter, 38.1%.

Fig. 10: Average Correlations Robust Equity Long/Short vs. S&P 500 index, Aug 1990-Jun 2014

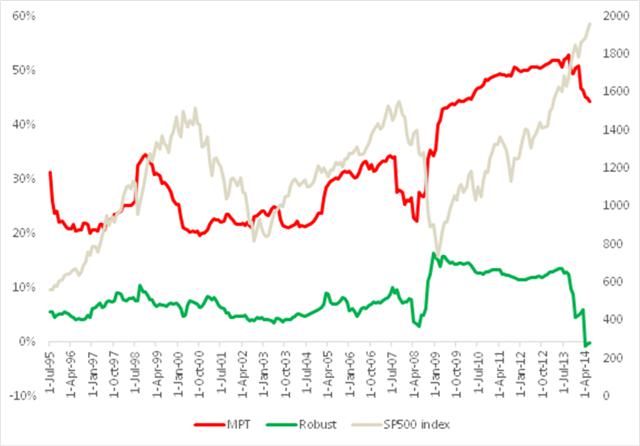
Source: Yahoo Finance, 2014

The much lower average correlation levels mean that it is possible to construct fully diversified portfolios in the robust portfolio framework with fewer assets than in the traditional MPT framework. Put another way, a robust portfolio with a small number of assets will typically produce higher returns with lower volatility than a traditional, optimal portfolio (in the MPT sense) constructed using the same underlying assets.

In terms of correlation of the portfolio itself, we find that over the period from Aug 1990 to June 2014, the robust portfolio exhibits close to zero net correlation with the market. However, the summary result disguises yet another important advantage of the robust portfolio. From the scatterplot shown in Fig. 11, we can see that, in fact, the robust portfolio has a tendency to adjust its correlation according to market conditions. When the market is moving positively, the robust portfolio tends to have a positive correlation, while during periods when the market is in decline, the robust portfolio tends to have a negative correlation.

Fig. 11: Correlation between Robust Equity Long/Short vs. S&P 500 index, Aug 1990-Jun 2014

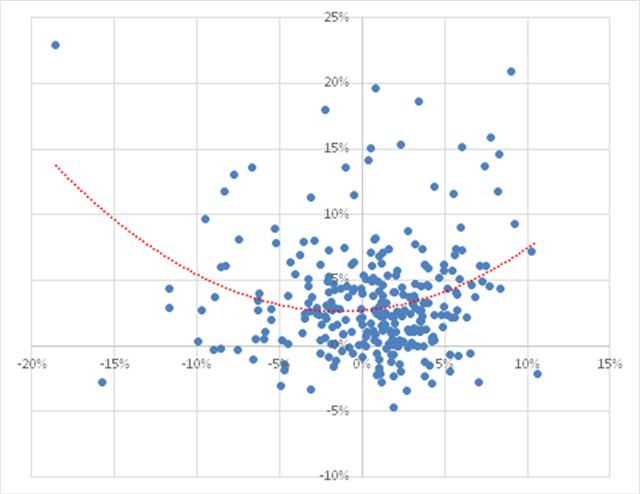
Source: Yahoo Finance, 2014

Optimal Robust Portfolios

The robust portfolio referenced in our discussion hitherto is a naïve portfolio with equal dollar allocations to each individual equity strategy. What happens if we apply MPT to the equity strategy constituents and construct an “optimal” (in the mean-variance sense) robust portfolio?

The results from this procedure are summarized in Fig. 12, which shows the evolution of the efficient frontier, traversed by the risk/return path of the optimal robust portfolio. Both show considerable variability. In fact, however, both the frontier and optimal portfolio are far more stable than their equivalents for the traditional MPT strategy.

Fig. 12: Time Evolution of the Efficient Frontier and Optimal Robust Portfolio

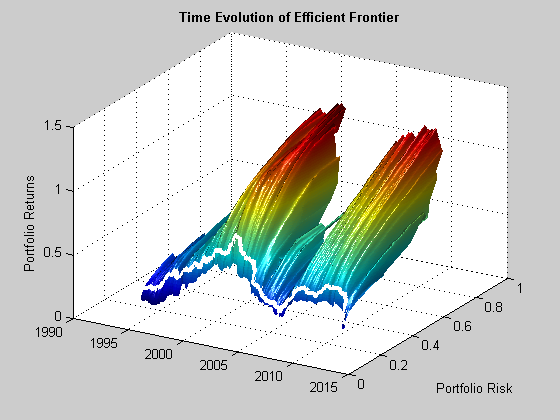
Source: MathWorks Inc.

Fig. 13 compares the performance of the naïve robust portfolio and optimal robust portfolio. The optimal portfolio does demonstrate a small, material improvement in risk-adjusted returns, but at the cost of an increase in the maximum drawdown. It is an open question as to whether the modest improvement in performance is sufficient to justify the additional portfolio turnover and commensurate trading cost and operational risk. The incremental benefits are relatively minor, because the equally weighted portfolio is already well-diversified due to the low average correlation in its constituent strategies.

Fig. 13: Naïve vs. Optimal Robust Portfolio Performance Aug 1990-Jun 2014

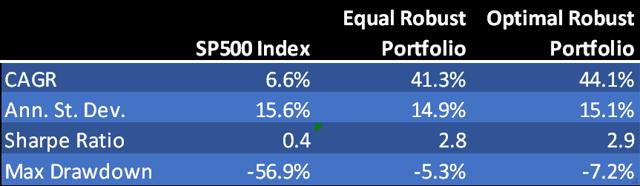
Source: Yahoo Finance, 2014

Conclusion

The limitations of MPT in terms of its underlying assumptions and implementation challenges limits its usefulness as a practical tool for investors looking to construct equity portfolios that will enable them to achieve their investment objectives. Rather than seeking to optimize risk-adjusted returns in the traditional way, investors may be better served by identifying important characteristics of strategy robustness and using these to create strategies for individual equities that perform robustly across a wide range of market conditions. By constructing portfolios composed of such strategies, rather than using the underlying equities, investors may achieve higher, more stable returns under a broad range of market conditions, including periods of high volatility or market drawdown.

¹ Optimal Versus Naive Diversification: How Inefficient is the 1/N Portfolio Strategy?, Victor DeMiguel, Lorenzo Garlappi and Raman Uppal, The Review of Financial Studies, Vol. 22, Issue 5, 2007.

September 14, 2018

More on Strategy Robustness

Commentators have made the point that a high % win rate is not enough.

Yes, you obviously want to pay attention to other performance metrics also, such as profit factor. In fact, there is no reason why you shouldn’t consider an objective function that explicitly combines various desirable performance measures, for example:

net profit * % win rate * profit factor

Another approach is to build the model using a data set spanning a different period. I did this with WFC using data from 1990, rather than 1970. Not only was the performance from 1990-2014 better, so too was the performance during the OOS period 1970-1989. Profit factor was 2.49 and %Win rate was 70% across the 44 year period from 1970. For the period from 1990, the performance metrics increase to 3.04 and 73%, respectively.

So in this case, it appears, a most robust strategy resulted from using less data, rather than more. At first this appears counterintuitive. But it’s quite possible for a strategy to be over-condition on behavior that is no longer relevant to the market today. Eliminating such conditioning can sometimes enable strategies to emerge that have greater longevity.

September 14, 2018

Optimizing Strategy Robustness

Below is the equity curve for an equity strategy I developed recently, implemented in WFC. The results appear outstanding: no losing years in over 20 years, profit factor of 2.76 and average win rate of 75%. Out-of-sample results (double blind) for 2013 and 2014: net returns of 27% and 16% YTD.

So far so good. However, if we take a step back through the earlier out of sample period, from 1970, the picture is rather less rosy:

Now, at this point, some of you will be saying: nothing to see here – it’s obviously just curve fitting. To which I would respond that I have seen successful strategies, including several hedge fund products, with far shorter and less impressive back-tests than the initial 20-year history I showed above.

That said, would you be willing to take the risk of trading a strategy such as this one? I would not: at the back of my mind would always be the concern that the market might easily revert to the conditions that applied during the 1970s and 1980’s. I expect many investors would share that concern.

But to the point of this post: most strategies are designed around the criterion of maximizing net profit. Occasionally you might come across someone who has considered risk, perhaps in the form of drawdown, or Sharpe ratio. But, in general, it’s all about optimizing performance.

Suppose that, instead of maximizing performance, your objective was to maximize the robustness of the strategy. What criteria would you use?

In my own research, I have used a great many different objective functions, often multi-dimensional. Correlation to the perfect equity curve, net profit / max drawdown and Sortino ratio are just a few examples. But if I had to guess, I would say that the criteria that tends to produce the most robust strategies and reliable out of sample performance is the maximization of the win rate, subject to a minimum number of trades.

I am not aware of a great deal of theory on this topic. I would be interested to learn of other readers’ experience.

September 11, 2018

How Not to Develop Trading Strategies – A Cautionary Tale

In his post on Multi-Market Techniques for Robust Trading Strategies (http://www.adaptrade.com/Newsletter/NL-MultiMarket.htm) Michael Bryant of Adaptrade discusses some interesting approaches to improving model robustness. One is to use data from several correlated assets to build the model, on the basis that if the algorithm works for several assets with differing price levels, that would tend to corroborate the system’s robustness. The second approach he advocates is to use data from the same asset series at different bars lengths. The example he uses @ES.D at 5, 7 and 9 minute bars. The argument in favor of this approach is the same as for the first, albeit in this case the underlying asset is the same.

I like Michael’s idea in principle, but I wanted to give you a sense of what can all too easily go wrong with GP modeling, even using techniques such as multi-time frame fitting and Monte Carlo simulation to improve robustness testing.

In the chart below I have extended the analysis back in time, beyond the 2011-2012 period that Michael used to build his original model. As you can see, most of the returns are generated in-sample, in the 2011-2012 period. As we look back over the period from 2007-2010, the results are distinctly unimpressive – the strategy basically trades sideways for four years.

How do Do It Right

In my view, there is only one, safe way to use GP to develop strategies. Firstly, you need to use a very long span of data – as much as possible, to fit your model. Only in this way can you ensure that the model has encountered enough variation in market conditions to stand a reasonable chance of being able to adapt to changing market conditions in future.

Secondly, you need to use two OOS period. The first OOS span of data, drawn from the start of the data series, is used in the normal way, to visually inspect the performance of the model. But the second span of OOS data, from more recent history, is NOT examined before the model is finalized. This is really important. Products like Adaptrade make it too easy for the system designer to “cheat”, by looking at the recent performance of his trading system “out of sample” and selecting models that do well in that period. But the very process of examining OOS performance introduces bias into the system. It would be like adding a line of code saying something like:

IF (model performance in OOS period > x) do the following….

I am quite sure if I posted a strategy with a line of code like that in it, it would immediately be shot down as being blatantly biased, and quite rightly so. But, if I look at the recent “OOS” performance and use it to select the model, I am effectively doing exactly the same thing.

That is why it is so important to have a second span of OOS data that it not only not used to build the model, but also is not used to assess performance, until after the final model selection is made. For that reason, the second OOS period is referred to as a “double blind” test.

That’s the procedure I followed to build my futures daytrading strategy: I used as much data as possible, dating from 2002. The first 20% of the each data set was used for normal OOS testing. But the second set of data, from Jan 2012 onwards, was my double-blind data set. Only when I saw that the system maintained performance in BOTH OOS periods was I reasonably confident of the system’s robustness.

This further explains why it is so challenging to develop higher frequency strategies using GP. Running even a very fast GP modeling system on a large span of high frequency data can take inordinate amounts of time.

The longest span of 5-min bar data that a GP system can handle would typically be around 5-7 years. This is probably not quite enough to build a truly robust system, although if you pick you time span carefully it might be (I generally like to use the 2006-2011 period, which has lots of market variation).

For 15 minute bar data, a well-designed GP system can usually handle all the available data you can throw at it – from 1999 in the case of the Emini, for instance.

Why I don’t Like Fitting Models over Short Time Spans

The risks of fitting models to data in short time spans are intuitively obvious. If you happen to pick a data set in which the market is in a strong uptrend, then your model is going to focus on that kind of market behavior. Subsequently, when the trend changes, the strategy will typically break down.
Monte Carlo simulation isn’t going to change much in this situation: sure, it will help a bit, perhaps, but since the resampled data is all drawn from the same original data set, in most cases the simulated paths will also show a strong uptrend – all that will be shown is that there is some doubt about the strength of the trend. But a completely different scenario, in which, say, the market drops by 10%, is unlikely to appear.

One possible answer to that problem, recommended by some system developers, is simply to rebuild the model when a breakdown is detected. While it’s true that a product like MSA can make detection easier, rebuilding the model is another question altogether. There is no guarantee that the kind of model that has worked hitherto can be re-tooled to work once again. In fact, there may be no viable trading system that can handle the new market dynamics.

Here is a case in point. We have a system that works well on 10 min bars in TF.D up until around May 2012, when MSA indicates a breakdown in strategy performance.

So now we try to fit a new model, along the pattern of the original model, taking account some of the new data. But it turns out to be just a Band-Aid – after a few more data points the strategy breaks down again, irretrievably.

This is typical of what often happens when you use GP to build a model using s short span of data. That’s why I prefer to use a long time span, even at lower frequency. The chances of being able to build a robust system that will adapt well to changing market conditions are much higher.

A Robust Emini Trading System

Here, for example is a GP system build on daily data in @ES.D from 1999 to 2011 (i.e. 2012 to 2014 is OOS).