Tag: S&P500 Index

Posted on

Backtest vs. Trading Reality

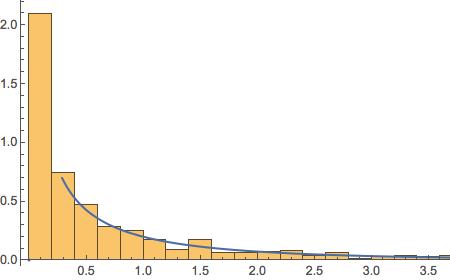
Kris Sidial, whose Twitter posts are often interesting, recently posted about the reality of trading profitability vs backtest performance, as follows:

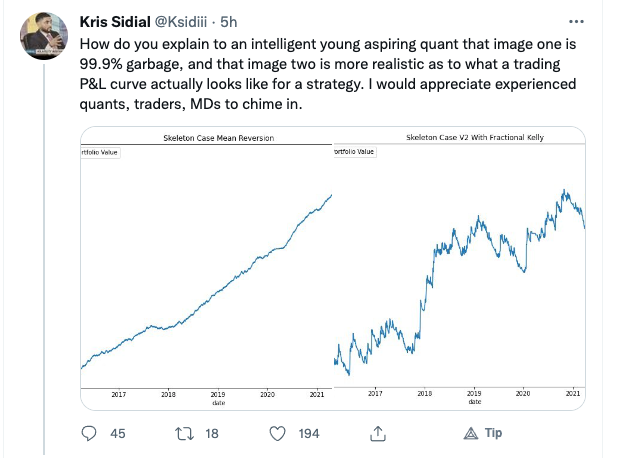
While I certainly agree that the latter example is more representative of a typical trader’s P&L, I don’t concur that the first P&L curve is necessarily “99.9% garbage”. There are many strategies that have equity curves that are smoother and more monotonic than those of Kris’s Skeleton Case V2 strategy. Admittedly, most of these lie in the area of high frequency, which is not Kris’s domain expertise. But there are also lower frequency strategies that produce results which are not dissimilar to those shown the first chart.

As a case in point, consider the following strategy for the S&P 500 E-Mini futures contract, described in more detail below. The strategy was developed using 15-minute bar data from 1999 to 2012, and traded live thereafter. The live and backtest performance characteristics are almost indistinguishable, not only in terms of rate of profit, but also in regard to strategy characteristics such as the no. of trades, % win rate and profit factor.

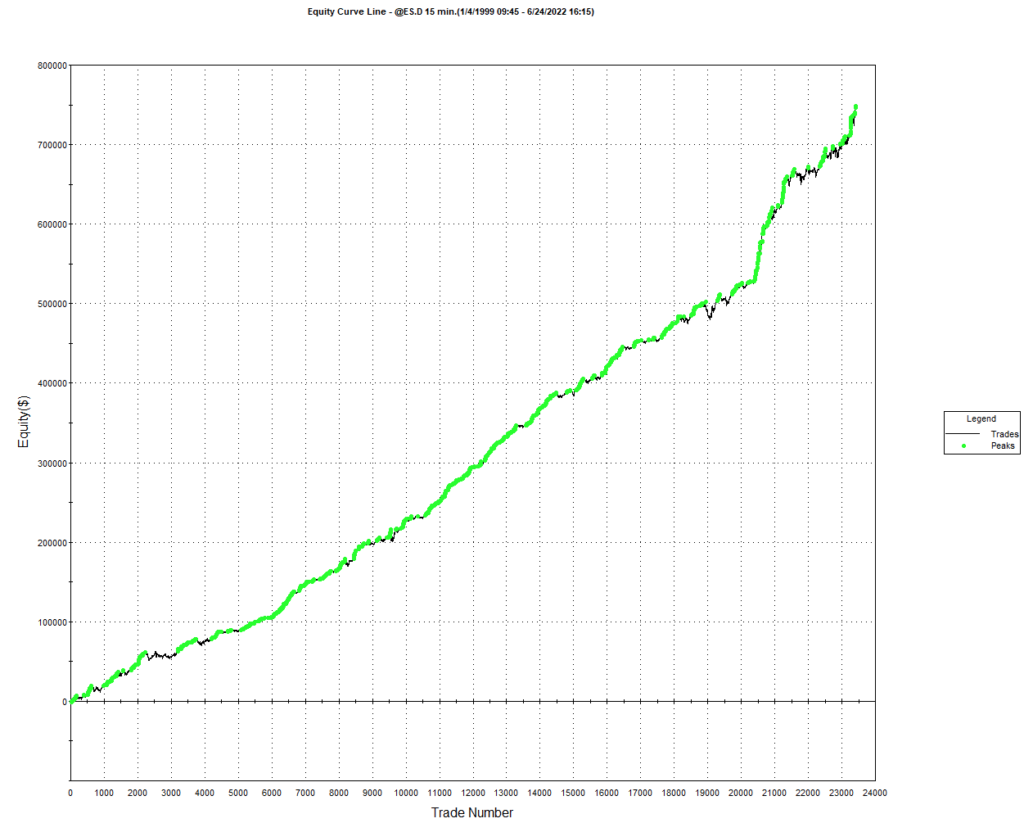
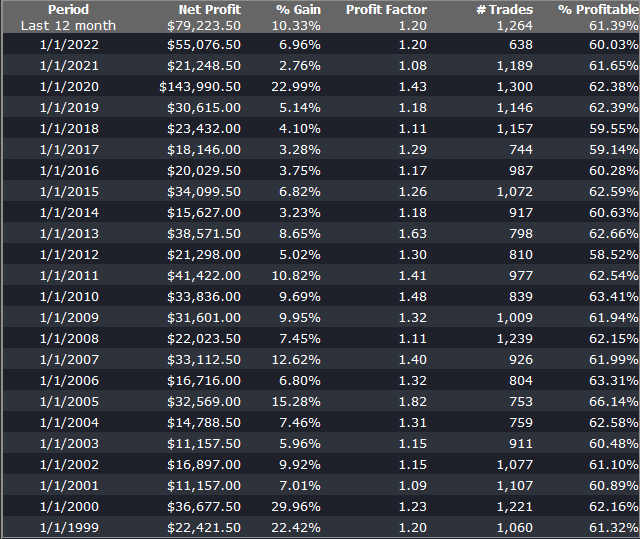
Just in case you think the picture is a little too rosy, I would point out that the average profit factor is 1.25, which means that the strategy is generating only 25% more in profits than losses. There will be big losing trades from time to time and long sequences of losses during which the strategy appears to have broken down. It takes discipline to resist the temptation to “fix” the strategy during extended drawdowns and instead rely on reversion to the mean rate of performance over the long haul. One source of comfort to the trader through such periods is that the 60% win rate means that the majority of trades are profitable.

As you read through the replies to Kris’s post, you will see that several of his readers make the point that strategies with highly attractive equity curves and performance characteristics are typically capital constrained. This is true in the case of this strategy, which I trade with a very modest amount of (my own) capital. Even trading one-lots in the E-Mini futures I occasionally experience missed trades, either on entry or exit, due to limit orders not being filled at the high or low of a bar. In scaling the strategy up to something more meaningful such as a 10-lot, there would be multiple partial fills to deal with. But I think it would be a mistake to abandon a high performing strategy such as this just because of an apparent capacity constraint. There are several approaches one can explore to address the issue, which may be enough to make the strategy scalable.

Where (as here) the issue of scalability relates to the strategy fill rate on limit orders, a good starting point is to compute the extreme hit rate, which is the proportion of trades that take place at the high or low of the bar. As a rule of thumb, for strategies running on typical low frequency infrastructure an extreme hit rate of 10% or less is manageable; anything above that level quickly becomes problematic. If the extreme hit rate is very high, e.g. 25% or more, then you are going to have to pay a great deal of attention to the issues of latency and order priority to make the strategy viable in practise. Ultimately, for a high frequency market making strategy, most orders are filled at the extreme of each “bar”, so almost all of the focus in on minimizing latency and maintaining a high queue priority, with all of the attendant concerns regarding trading hardware, software and infrastructure.

Next, you need a strategy for handling missed trades. You could, for example, decide to skip any entry trades that are missed, while manually entering unfilled exit trades at the market. Or you could post market orders for both entry and exit trades if they are not filled. An extreme solution would be to substitute market-if-touched orders for limit orders in your strategy code. But this would affect all orders generated by the system, not just the 10% at the high or low of the bar and is likely to have a very adverse affect on overall profitability, especially if the average trade is low (because you are paying an extra tick on entry and exit of every trade).

The above suggests that you are monitoring the strategy manually, running simulation and live versions side by side, so that you can pick up any trades that the strategy should have taken, but which have been missed. This may be practical for a strategy that trades during regular market hours, but not for one that also trades the overnight session.

An alternative approach, one that is commonly applied by systematic traders, is to automate the handling of missed trades. Typically the trader will set a parameter that converts a limit order to a market order X seconds after a limit price has been traded but not filled. Of course, this will result in paying up an extra tick (or more) to enter trades that perhaps would have been filled if one had waited longer than X seconds. It will have some negative impact on strategy profitability, but not too much if the extreme hit rate is low. I tend to use this method for exit trades, preferring to skip any entry trades that don’t get filled at the limit price.

Beyond these simple measures, there are several other ways to extend the capacity of the strategy. An obvious place to start is by evaluating strategy performance on different session times and bar lengths. So, in this case, we might look at deploying the strategy on both the day and night sessions. We can also evaluate performance on bars of different length. This will give different entry and exit points for individual trades and trades that are at the extreme of a bar on one timeframe may not be at the high or low of a bar on the other timescale. For example, here is the (simulated) performance of the strategy on 13 minute bars:

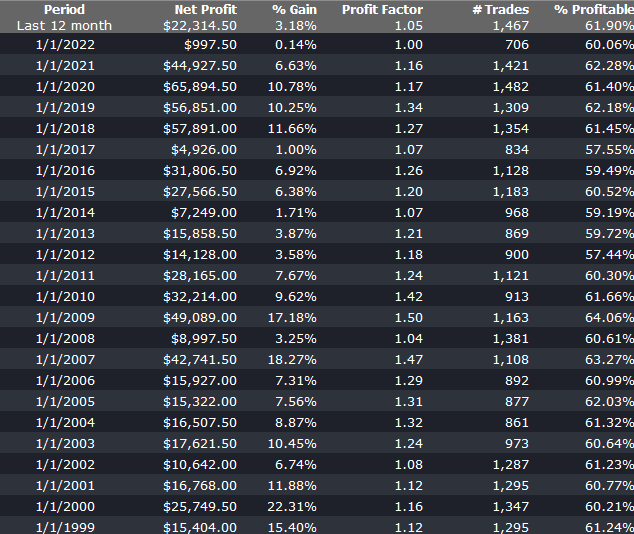
There is a reason for choosing a bar interval such as 13 minutes, rather than the more commonplace 5- or 10 minutes, as explained in this post:

Trading Prime Market Cycles

Finally, it is worth exploring whether the strategy can be applied to other related markets such as NQ futures, for example. Typically this will entail some change to the strategy code to reflect the difference in price levels, but the thrust of the strategy logic will be similar. Another approach is to use the signals from the current strategy as inputs – i.e. alpha generators – for a derivative strategy, such as trading the SPY ETF based on signals from the ES strategy. The performance of the derived strategy may not be as good, but in a product like SPY the capacity might be larger.

Posted on

Range-Based EGARCH Option Pricing Models (REGARCH)

The research in this post and the related paper on Range Based EGARCH Option pricing Models is focused on the innovative range-based volatility models introduced in Alizadeh, Brandt, and Diebold (2002) (hereafter ABD).  We develop new option pricing models using multi-factor diffusion approximations couched within this theoretical framework and examine their properties in comparison with the traditional Black-Scholes model.

The two-factor version of the model, which I have applied successfully in various option arbitrage strategies, encapsulates the intuively appealing idea of a trending long term mean volatility process, around which oscillates a mean-reverting, transient volatility process.  The option pricing model also incorporates asymmetry/leverage effects and well as correlation effects between the asset return and volatility processes, which results in a volatility skew.

The core concept behind Range-Based Exponential GARCH model is Log-Range estimator discussed in an earlier post on volatility metrics, which contains a lengthy exposition of various volatility estimators and their properties. (Incidentally, for those of you who requested a copy of my paper on Estimating Historical Volatility, I have updated the post to include a link to the pdf).

SSALGOTRADING AD

We assume that the log stock price s follows a drift-less Brownian motion ds = sdW. The volatility of daily log returns, denoted h= s/sqrt(252), is assumed constant within each day, at ht from the beginning to the end of day t, but is allowed to change from one day to the next, from ht at the end of day t to ht+1 at the beginning of day t+1.  Under these assumptions, ABD show that the log range, defined as:

is to a very good approximation distributed as

where N[m; v] denotes a Gaussian distribution with mean m and variance v. The above equation demonstrates that the log range is a noisy linear proxy of log volatility ln ht.  By contrast, according to the results of Alizadeh, Brandt,and Diebold (2002), the log absolute return has a mean of 0.64 + ln ht and a variance of 1.11. However, the distribution of the log absolute return is far from Gaussian.  The fact that both the log range and the log absolute return are linear log volatility proxies (with the same loading of one), but that the standard deviation of the log range is about one-quarter of the standard deviation of the log absolute return, makes clear that the range is a much more informative volatility proxy. It also makes sense of the finding of Andersen and Bollerslev (1998) that the daily range has approximately the same informational content as sampling intra-daily returns every four hours.

Except for the model of Chou (2001), GARCH-type volatility models rely on squared or absolute returns (which have the same information content) to capture variation in the conditional volatility ht. Since the range is a more informative volatility proxy, it makes sense to consider range-based GARCH models, in which the range is used in place of squared or absolute returns to capture variation in the conditional volatility. This is particularly true for the EGARCH framework of Nelson (1990), which describes the dynamics of log volatility (of which the log range is a linear proxy).

ABD consider variants of the EGARCH framework introduced by Nelson (1990). In general, an EGARCH(1,1) model performs comparably to the GARCH(1,1) model of Bollerslev (1987).  However, for stock indices the in-sample evidence reported by Hentschel (1995) and the forecasting performance presented by Pagan and Schwert (1990) show a slight superiority of the EGARCH specification. One reason for this superiority is that EGARCH models can accommodate asymmetric volatility (often called the “leverage effect,” which refers to one of the explanations of asymmetric volatility), where increases in volatility are associated more often with large negative returns than with equally large positive returns.

The one-factor range-based model (REGARCH 1)  takes the form:

where the returns process Rt is conditionally Gaussian: Rt ~ N[0, ht2]

and the process innovation is defined as the standardized deviation of the log range from its expected value:

Following Engle and Lee (1999), ABD also consider multi-factor volatility models.  In particular, for a two-factor range-based EGARCH model (REGARCH2), the conditional volatility dynamics) are as follows:

and

where ln qt can be interpreted as a slowly-moving stochastic mean around which log volatility  ln ht makes large but transient deviations (with a process determined by the parameters kh, fh and dh).

The parameters q, kq, fq and dq determine the long-run mean, sensitivity of the long run mean to lagged absolute returns, and the asymmetry of absolute return sensitivity respectively.

The intuition is that when the lagged absolute return is large (small) relative to the lagged level of volatility, volatility is likely to have experienced a positive (negative) innovation. Unfortunately, as we explained above, the absolute return is a rather noisy proxy of volatility, suggesting that a substantial part of the volatility variation in GARCH-type models is driven by proxy noise as opposed to true information about volatility. In other words, the noise in the volatility proxy introduces noise in the implied volatility process. In a volatility forecasting context, this noise in the implied volatility process deteriorates the quality of the forecasts through less precise parameter estimates and, more importantly, through less precise estimates of the current level of volatility to which the forecasts are anchored.

read more…

2-Factor REGARCH Model for the S&P500 Index
Posted on

On Testing Direction Prediction Accuracy


As regards the question of forecasting accuracy discussed in the paper on Forecasting Volatility in the S&P 500 Index, there are two possible misunderstandings here that need to be cleared up.  These arise from remarks by one commentator  as follows:

“An above 50% vol direction forecast looks good,.. but “direction” is biased when working with highly skewed distributions!   ..so it would be nice if you could benchmark it against a simple naive predictors to get a feel for significance, -or- benchmark it with a trading strategy and see how the risk/return performs.”

(i) The first point is simple, but needs saying: the phrase “skewed distributions” in the context of volatility modeling could easily be misconstrued as referring to the volatility skew. This, of course, is used to describe to the higher implied vols seen in the Black-Scholes prices of OTM options. But in the Black-Scholes framework volatility is constant, not stochastic, and the “skew” referred to arises in the distribution of the asset return process, which has heavier tails than the Normal distribution (excess Kurtosis and/or skewness). I realize that this is probably not what the commentator meant, but nonetheless it’s worth heading that possible misunderstanding off at the pass, before we go on.

SSALGOTRADING AD

(ii) I assume that the commentator was referring to the skewness in the volatility process, which is characterized by the LogNormal distribution. But the forecasting tests referenced in the paper are tests of the ability of the model to predict the direction of volatility, i.e. the sign of the change in the level of volatility from the current period to the next period. Thus we are looking at, not a LogNormal distribution, but the difference in two LogNormal distributions with equal mean – and this, of course, has an expectation of zero. In other words, the expected level of volatility for the next period is the same as the current period and the expected change in the level of volatility is zero. You can test this very easily for yourself by generating a large number of observations from a LogNormal process, taking the difference and counting the number of positive and negative changes in the level of volatility from one period to the next. You will find, on average, half the time the change of direction is positive and half the time it is negative.

For instance, the following chart shows the distribution of the number of positive changes in the level of a LogNormally distributed random variable with mean and standard deviation of 0.5, for a sample of 1,000 simulations, each of 10,000 observations.  The sample mean (5,000.4) is very close to the expected value of 5,000.

Distribution Number of Positive Direction Changes

So, a naive predictor will forecast volatility to remain unchanged for the next period and by random chance approximately half the time volatility will turn out to be higher and half the time it will turn out to be lower than in the current period. Hence the default probability estimate for a positive change of direction is 50% and you would expect to be right approximately half of the time. In other words, the direction prediction accuracy of the naive predictor is 50%. This, then, is one of the key benchmarks you use to assess the ability of the model to predict market direction. That is what test statistics like Theil’s-U does – measures the performance relative to the naive predictor. The other benchmark we use is the change of direction predicted by the implied volatility of ATM options.
In this context, the model’s 61% or higher direction prediction accuracy is very significant (at the 4% level in fact) and this is reflected in the Theil’s-U statistic of 0.82 (lower is better). By contrast, Theil’s-U for the Implied Volatility forecast is 1.46, meaning that IV is a much worse predictor of 1-period-ahead changes in volatility than the naive predictor.

On its face, it is because of this exceptional direction prediction accuracy that a simple strategy is able to generate what appear to be abnormal returns using the change of direction forecasts generated by the model, as described in the paper. In fact, the situation is more complicated than that, once you introduce the concept of a market price of volatility risk.

 

Posted on

Market Timing in the S&P 500 Index Using Volatility Forecasts

There has been a good deal of interest in the market timing ideas discussed in my earlier blog post Using Volatility to Predict Market Direction, which discusses the research of Diebold and Christoffersen into the sign predictability induced by volatility dynamics.  The ideas are thoroughly explored in a QuantNotes article from 2006, which you can download here.

There is a follow-up article from 2006 in which Christoffersen, Diebold, Mariano and Tay develop the ideas further to consider the impact of higher moments of the asset return distribution on sign predictability and the potential for market timing in international markets (download here).

Trading Strategy
To illustrate some of the possibilities of this approach, we constructed a simple market timing strategy in which a position was taken in the S&P 500 index or in 90-Day T-Bills, depending on an ex-ante forecast of positive returns from the logit regression model (and using an expanding window to estimate the drift coefficient).  We assume that the position is held for 30 days and rebalanced at the end of each period.  In this test we make no allowance for market impact, or transaction costs.

Results
Annual returns for the strategy and for the benchmark S&P 500 Index are shown in the figure below.  The strategy performs exceptionally well in 1987, 1989 and 1995, when the ratio between expected returns and volatility remains close to optimum levels and the direction of the S&P 500 Index is highly predictable,  Of equal interest is that the strategy largely avoids the market downturn of 2000-2002 altogether, a period in which sign probabilities were exceptionally low.

SSALGOTRADING AD

In terms of overall performance, the model enters the market in 113 out of a total of 241 months (47%) and is profitable in 78 of them (69%).  The average gain is 7.5% vs. an average loss of –4.11% (ratio 1.83).  The compound annual return is 22.63%, with an annual volatility of 17.68%, alpha of 14.9% and Sharpe ratio of 1.10.

The under-performance of the strategy in 2003 is explained by the fact that direction-of-change probabilities were rising from a very low base in Q4 2002 and do not reach trigger levels until the end of the year.  Even though the strategy out-performed the Index by a substantial margin of 6% , the performance in 2005 is of concern as market volatility was very low and probabilities overall were on a par with those seen in 1995.  Further tests are required to determine whether the failure of the strategy to produce an exceptional performance on par with 1995 was the result of normal statistical variation or due to changes in the underlying structure of the process requiring model recalibration.

Future Research & Development
The obvious next step is to develop the approach described above to formulate trading strategies based on sign forecasting in a universe of several assets, possibly trading binary options.  The approach also has potential for asset allocation, portfolio theory and risk management applications.

Market Timing in the S&P500 Index
Market Timing in the S&P500 Index
Posted on

Beating the S&P500 Index with a Low Convexity Portfolio

What is Beta Convexity?

Beta convexity is a measure of how stable a stock beta is across market regimes.  The essential idea is to evaluate the beta of a stock during down-markets, separately from periods when the market is performing well.  By choosing a portfolio of stocks with low beta-convexity we seek to stabilize the overall risk characteristics of our investment portfolio.

A primer on beta convexity and its applications is given in the following post:

 

 

 

 

 

 

 

 

 

 

In this post I am going to use the beta-convexity concept to construct a long-only equity portfolio capable of out-performing the benchmark S&P 500 index.

The post is in two parts.  In the first section I outline the procedure in Mathematica for downloading data and creating a matrix of stock returns for the S&P 500 membership.  This is purely about the mechanics, likely to be of interest chiefly to Mathematica users. The code deals with the issues of how to handle stocks with multiple different start dates and missing data, a problem that the analyst is faced with on a regular basis.  Details are given in the pdf below. Let’s skip forward to the analysis.

Portfolio Formation & Rebalancing

We begin by importing the data saved using the data retrieval program, which comprises a matrix of (continuously compounded) monthly returns for the S&P500 Index and its constituent stocks.  We select a portfolio size of 50 stocks, a test period of 20 years, with a formation period of 60 months and monthly rebalancing.

In the processing stage, for each month in our 20-year test period we  calculate the beta convexity for each index constituent stock and select the 50 stocks that have the lowest beta-convexity during the prior 5-year formation period.  We then compute the returns for an equally weighted basket of the chosen stocks over the following month.  After that, we roll forward one month and repeat the exercise.

It turns out that beta-convexity tends to be quite unstable, as illustrated for a small sample of component stocks in the chart below:

A snapshot of estimated convexity factors is shown in the following table.  As you can see, there is considerable cross-sectional dispersion in convexity, in addition to time-series dependency.

At any point in time the cross-sectional dispersion is well described by a Weibull distribution, which passes all of the usual goodness-of-fit tests.

Performance Results

We compare the annual returns and standard deviation of the low convexity portfolio with the S&P500 benchmark in the table below. The results indicate that the average gross annual return of a low-convexity portfolio of 50 stocks is more than double that of the benchmark, with a comparable level of volatility. The portfolio also has slightly higher skewness and kurtosis than the benchmark, both desirable characteristics.

 

Portfolio Alpha & Beta Estimation

Using the standard linear CAPM model we estimate the annual alpha of the low-convexity portfolio to be around 7.39%, with a beta of 0.89.

Beta Convexity of the Low Convexity Portfolio

As we might anticipate, the beta convexity of the portfolio is very low since it comprises stocks with the lowest beta-convexity:

Conclusion: Beating the Benchmark S&P500 Index

Using a beta-convexity factor model, we are able to construct a small portfolio that matches the benchmark index in terms of volatility, but with markedly superior annual returns.  Larger portfolios offering greater liquidity produce slightly lower alpha, but a 100-200 stock portfolio typically produce at least double the annual rate of return of the benchmark over the 20-year test period.

For those interested, we shall shortly be offering a low-convexity strategy on our Systematic Algotrading platform – see details below:

Section on Data Retrieval and Processing

Data Retrieval