Statistical Arbitrage with Synthetic Data
In my last post I mapped out how one could test the reliability of a single stock strategy (for the S&P 500 Index) using synthetic data generated by the new algorithm I developed.
As this piece of research follows a similar path, I won’t repeat all those details here. The key point addressed in this post is that not only are we able to generate consistent open/high/low/close prices for individual stocks, we can do so in a way that preserves the correlations between related securities. In other words, the algorithm not only replicates the time series properties of individual stocks, but also the cross-sectional relationships between them. This has important applications for the development of portfolio strategies and portfolio risk management.
KO-PEP Pair
To illustrate this I will use synthetic daily data to develop a pairs trading strategy for the KO-PEP pair.
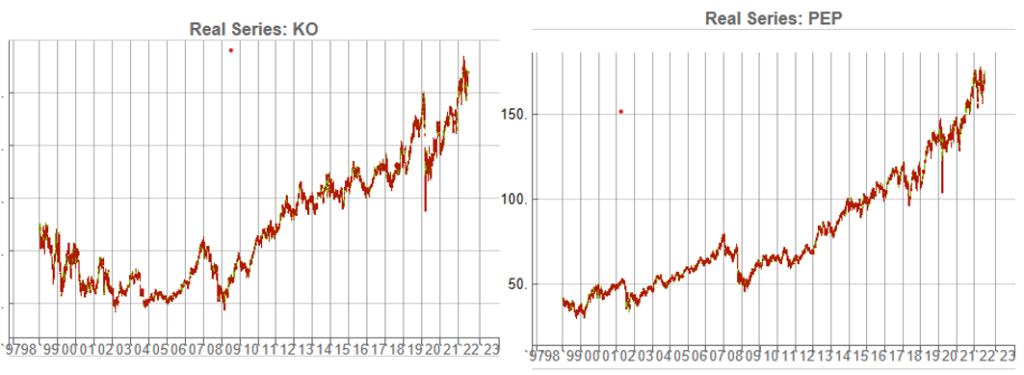
The two price series are highly correlated, which potentially makes them a suitable candidate for a pairs trading strategy.
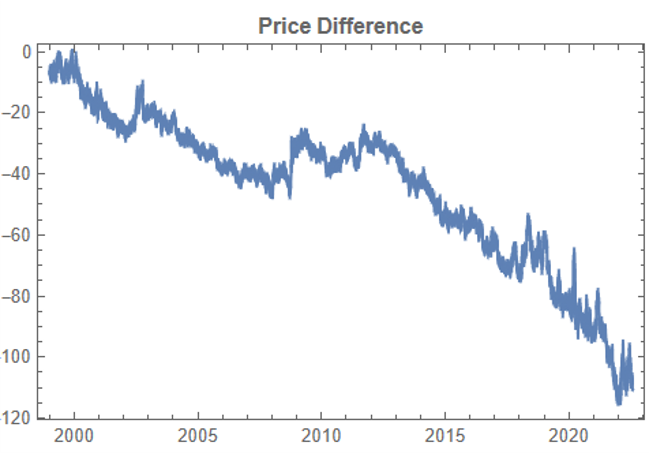
There are numerous ways to trade a pairs spread such as dollar neutral or beta neutral, but in this example I am simply going to look at trading the price difference. This is not a true market neutral approach, nor is the price difference reliably stationary. However, it will serve the purpose of illustrating the methodology.
Obviously it is crucial that the synthetic series we create behave in a way that replicates the relationship between the two stocks, so that we can use it for strategy development and testing. Ideally we would like to see high correlations between the synthetic and original price series as well as between the pairs of synthetic price data.
We begin by using the algorithm to generate 100 synthetic daily price series for KO and PEP and examine their properties.
Correlations
As we saw previously, the algorithm is able to generate synthetic data with correlations to the real price series ranging from below zero to close to 1.0:
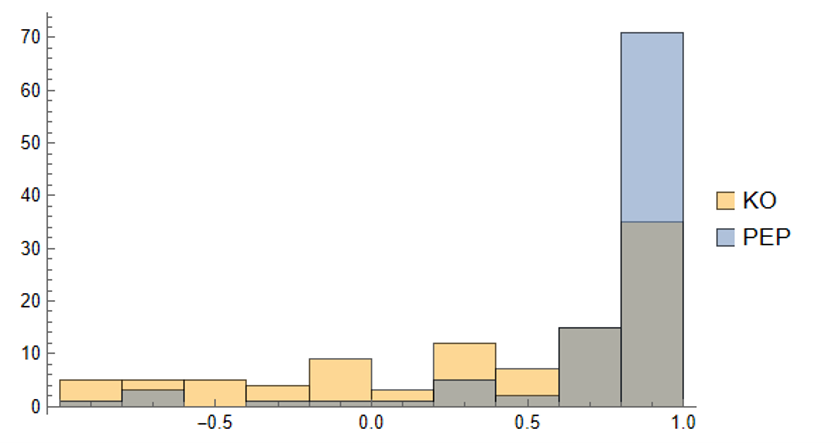
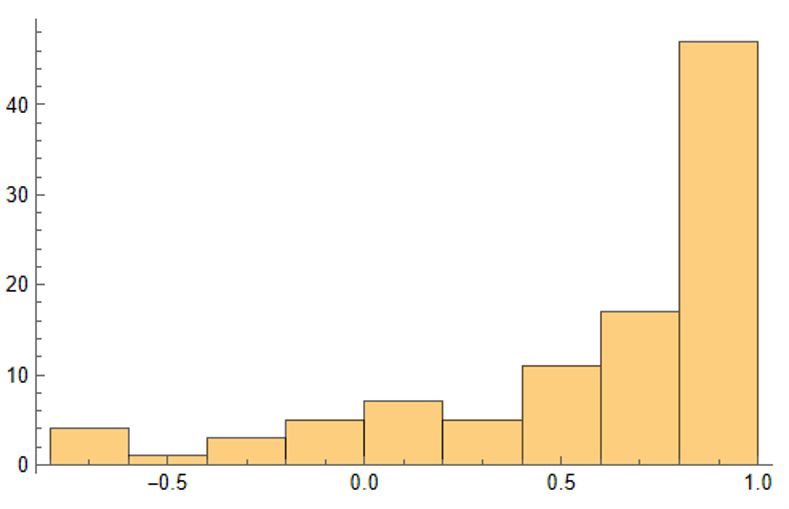
The crucial point, however, is that the algorithm has been designed to also preserve the cross-sectional correlation between the pairs of synthetic KO-PEP data, just as in the real data series:
Some examples of highly correlated pairs of synthetic data are shown in the plots below:
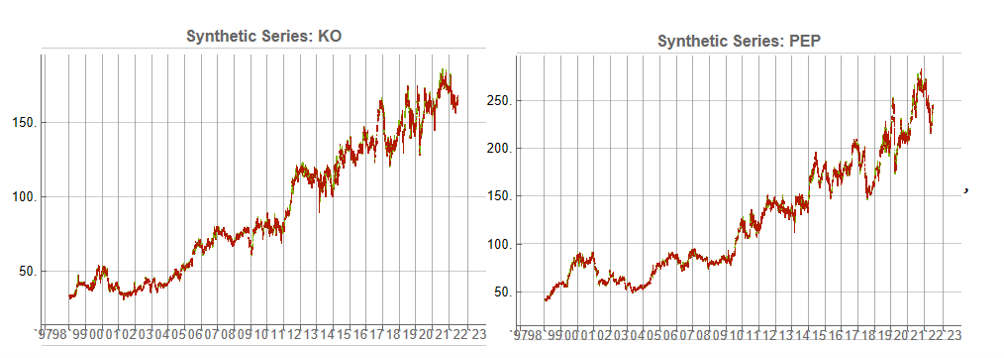
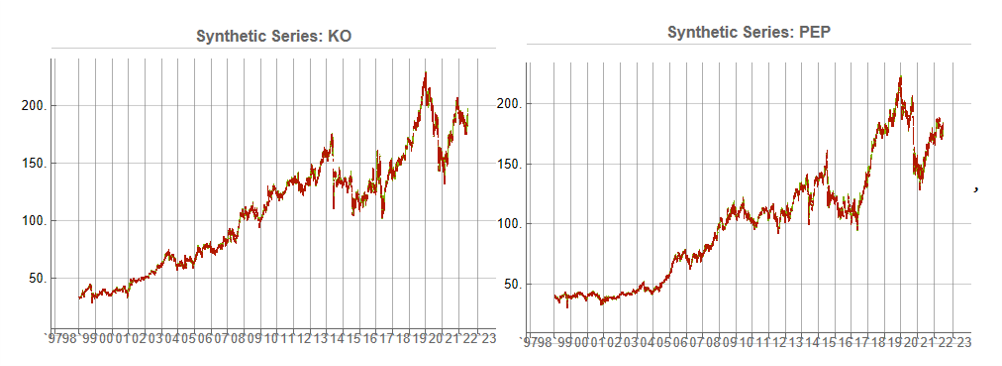
In addition to correlation, we might also want to consider the price differences between the pairs of synthetic series, since the strategy will be trading that price difference, in the simple approach adopted here. We could, for example, select synthetic pairs for which the divergence in the price difference does not become too large, on the assumption that the series difference is stationary. While that approach might well be reasonable in other situations, here an assumption of stationarity would be perhaps closer to wishful thinking than reality. Instead we can use of selection of synthetic pairs with high levels of cross-correlation, as we all high levels of correlation with the real price data. We can also select for high correlation between the price differences for the real and synthetic price series.
Strategy Development & WFO Testing
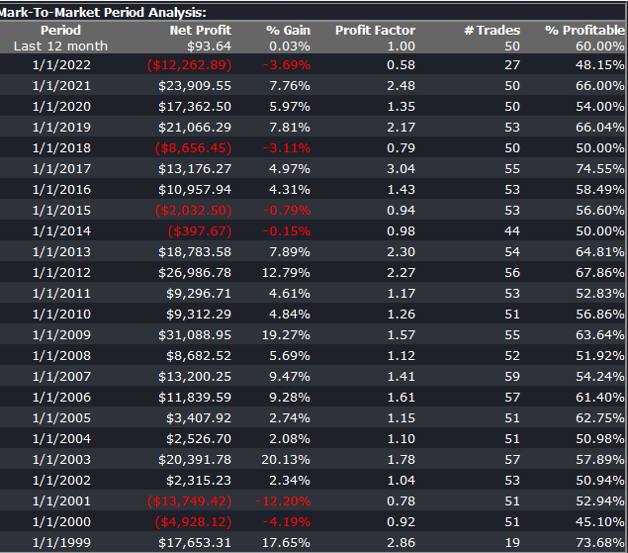
Once again we follow the procedure for strategy development outline in the previous post, except that, in addition to a selection of synthetic price difference series we also include 14-day correlations between the pairs. We use synthetic daily synthetic data from 1999 to 2012 to build the strategy and use the data from 2013 onwards for testing/validation. Eventually, after 50 generations we arrive at the result shown in the figure below:
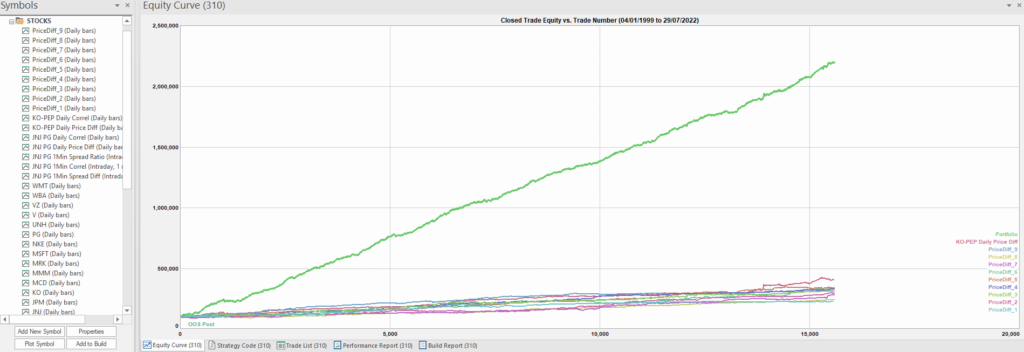
As before, the equity curve for the individual synthetic pairs are shown towards the bottom of the chart, while the aggregate equity curve, which is a composition of the results for all none synthetic pairs is shown above in green. Clearly the results appear encouraging.
As a final step we apply the WFO analysis procedure described in the previous post to test the performance of the strategy on the real data series, using a variable number in-sample and out-of-sample periods of differing size. The results of the WFO cluster test are as follows:
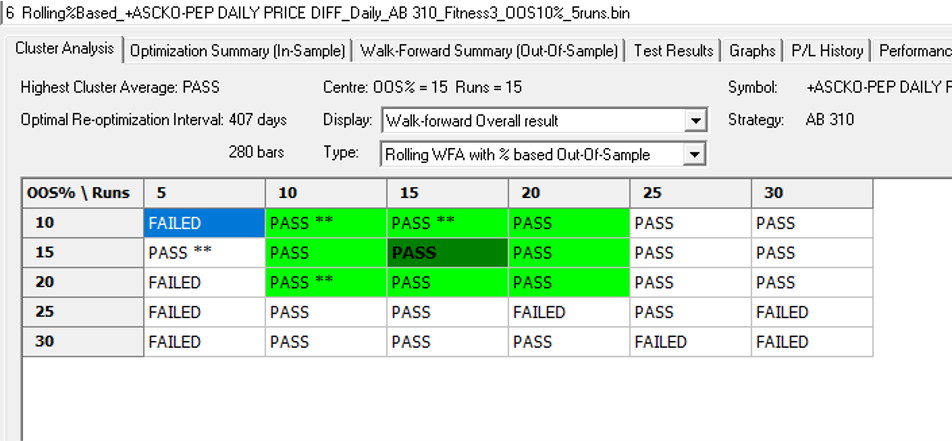
The results are no so unequivocal as for the strategy developed for the S&P 500 index, but would nonethless be regarded as acceptable, since the strategy passes the great majority of the tests (in addition to the tests on synthetic pairs data).
The final results appear as follows:
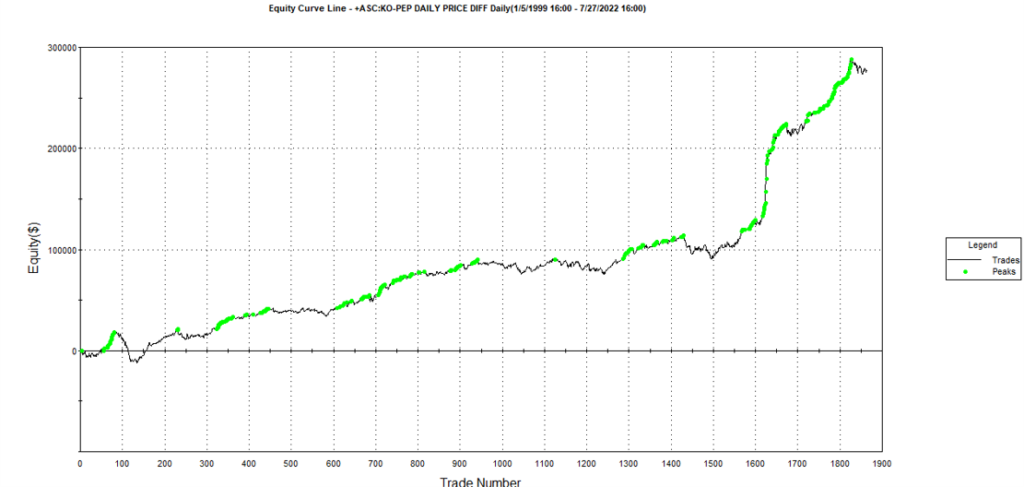
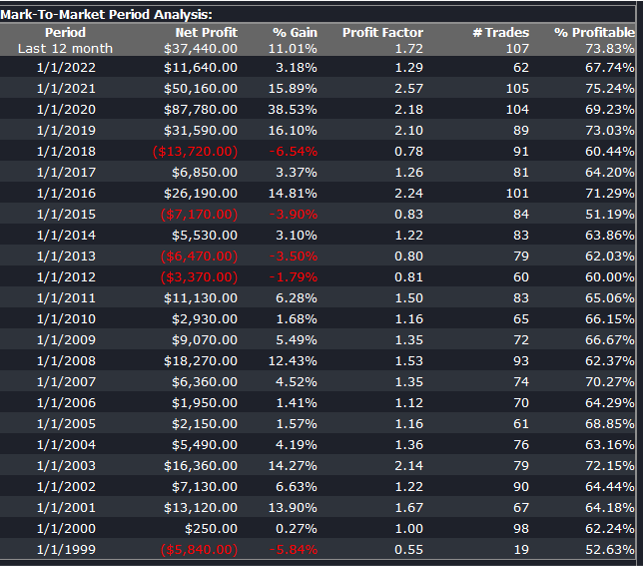
Conclusion
We have demonstrated how the algorithm can be used to generate synthetic price series the preserve not only the important time series properties, but also the cross-sectional properties between series for correlated securities. This important feature has applications in the development of statistical arbitrage strategies, portfolio construction methodology and in portfolio risk management.
Developing Trading Strategies With Synthetic Data
One of the main criticisms levelled at systematic trading over the last few years is that the over-use of historical market data has tended to produce curve-fitted strategies that perform poorly out of sample in a live trading environment. This is indeed a valid criticism – given enough attempts one is bound to arrive eventually at a strategy that performs well in backtest, even on a holdout data sample. But that by no means guarantees that the strategy will continue to perform well going forward.
The solution to the problem has been clear for some time: what is required is a method of producing synthetic market data that can be used to build a strategy and test it under a wide variety of simulated market conditions. A strategy built in this way is more likely to survive the challenge of live trading than one that has been developed using only a single historical data path.
The problem, however, has been in implementation. Up until now all the attempts to produce credible synthetic price data have failed, for one reason or another, as I described in an earlier post:
I have been able to devise a completely new algorithm for generating artificial price series that meet all of the key requirements, as follows:
- Computational simplicity & efficiency. Important if we are looking to mass-produce synthetic series for a large number of assets, for a variety of different applications. Some deep learning methods would struggle to meet this requirement, even supposing that transfer learning is possible.
- The ability to produce price series that are internally consistent (i.e High > Low, etc) in every case .
- Should be able to produce a range of synthetic series that vary widely in their correspondence to the original price series. In some case we want synthetic price series that are highly correlated to the original; in other cases we might want to test our investment portfolio or risk control systems under extreme conditions never before seen in the market.
- The distribution of returns in the synthetic series should closely match the historical series, being non-Gaussian and with “fat-tails”.
- The ability to incorporate long memory effects in the sequence of returns.
- The ability to model GARCH effects in the returns process.
This means that we are now in a position to develop trading strategies without any direct reference to the underlying market data. Consequently we can then use all of the real market data for out-of-sample back-testing.
Developing a Trading Strategy for the S&P 500 Index Using Synthetic Market Data
To illustrate the procedure I am going to use daily synthetic price data for the S&P 500 Index over the period from Jan 1999 to July 2022. Details of the the characteristics of the synthetic series are given in the post referred to above.
Because we want to create a trading strategy that will perform under market conditions close to those currently prevailing, I will downsample the synthetic series to include only those that correlate quite closely, i.e. with a minimum correlation of 0.75, with the real price data.
Why do this? Surely if we want to make a strategy as robust as possible we should use all of the synthetic data series for model development?
The reason is that I believe that some of the more extreme adverse scenarios generated by the algorithm may occur quite rarely, perhaps once in every few decades. However, I am principally interested in a strategy that I can apply under current market conditions and I am prepared to take my chances that the worst-case scenarios are unlikely to come about any time soon. This is a major design decision, one that you may disagree with. Of course, one could make use of every available synthetic data series in the development of the trading model and by doing so it is likely that you would produce a model that is more robust. But the training could take longer and the performance during normal market conditions may not be as good.
Having generated the price series, the process I am going to follow is to use genetic programming to develop trading strategies that will be evaluated on all of the synthetic data series simultaneously. I will then use the performance of the aggregate portfolio, i.e. the outcome of all of the trades generated by the strategy when applied to all of the synthetic series, to assess the overall performance. In order to be considered, candidate strategies have to perform well under all of the different market scenarios, or at least the great majority of them. This ensures that the strategy is likely to prove more robust across different types of market conditions, rather than on just the single type of market scenario observed in the real historical series.
As usual in these cases I will reserve a portion (10%) of each data series for testing each strategy, and a further 10% sample for out-of-sample validation. This isn’t strictly necessary: since the real data series has not be used directly in the development of the trading system, we can later test the strategy on all of the historical data and regard this as an out-of-sample backtest.
To implement the procedure I am going to use Mike Bryant’s excellent Adaptrade Builder software.
This is an exemplar of outstanding software engineering and provides a broad range of features for generating trading strategies of every kind. One feature of Builder that is particularly useful in this context is its ability to construct strategies and test them on up to 20 data series concurrently. This enables us to develop a strategy using all of the synthetic data series simultaneously, showing the performance of each individual strategy as well for as the aggregate portfolio.
After evolving strategies for 50 generations we arrive at the following outcome:
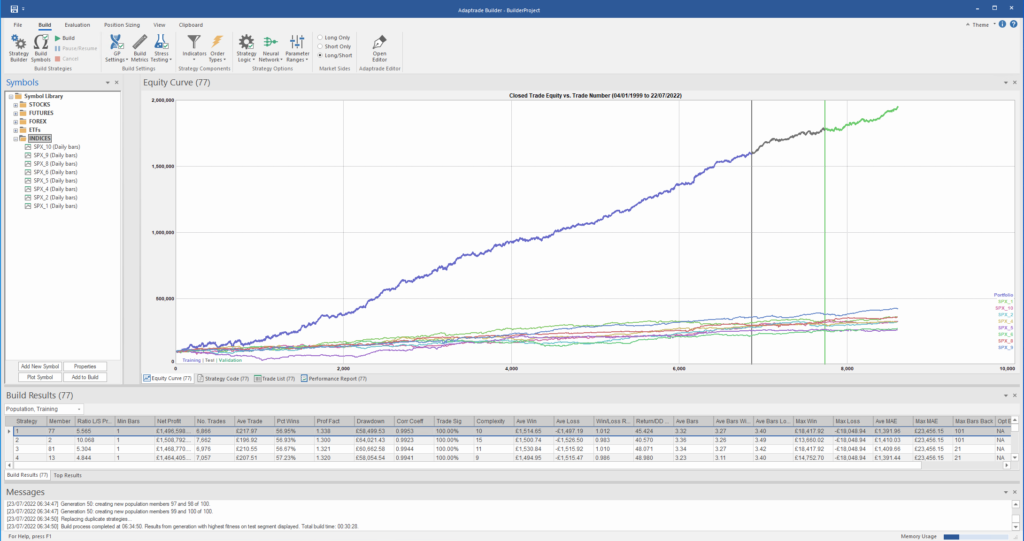
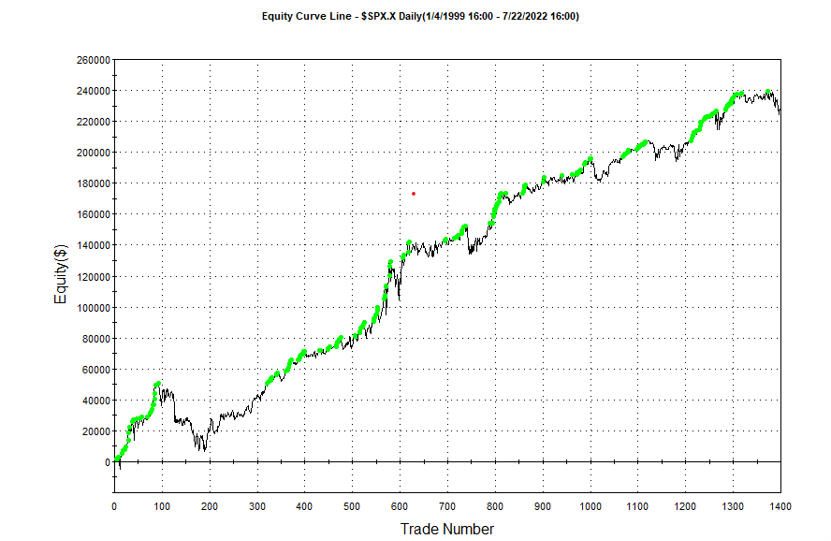
The equity curve for the aggregate portfolio is shown in blue, while the equity curves for the strategy applied to individual synthetic data series are shown towards the bottom of the chart. Of course, the performance of the aggregate portfolio appears much superior to any of the individual strategies, because it is effectively the arithmetic sum of the individual equity curves. And just because the aggregate portfolio appears to perform well both in-sample and out-of-sample, that doesn’t imply that the strategy works equally well for every individual market scenario. In some scenarios it performs better than in others, as can be observed from the individual equity curves.
But, in any case, our objective here is not to create a stock portfolio strategy, but rather to trade a single asset – the S&P 500 Index. The role of the aggregate portfolio is simply to suggest that we may have found a strategy that is sufficiently robust to work well across a variety of market conditions, as represented by the various synthetic price series.
Builder generates code for the strategies it evolves in a number of different languages and in this case we take the EasyLanguage code for the fittest strategy #77 and apply it to a daily chart for the S&P 500 Index – i.e. the real data series – in Tradestation, with the following results:
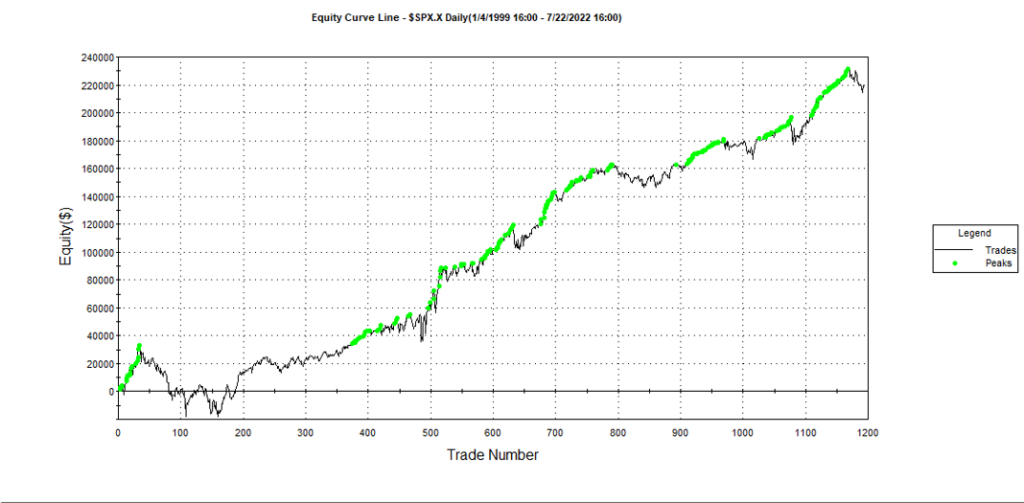
The strategy appears to work well “out-of-the-box”, i,e, without any further refinement. So our quest for a robust strategy appears to have been quite successful, given that none of the 23-year span of real market data on which the strategy was tested was used in the development process.
We can take the process a little further, however, by “optimizing” the strategy. Traditionally this would mean finding the optimal set of parameters that produces the highest net profit on the test data. But this would be curve fitting in the worst possible sense, and is not at all what I am suggesting.
Instead we use a procedure known as Walk Forward Optimization (WFO), as described in this post:
The goal of WFO is not to curve-fit the best parameters, which would entirely defeat the object of using synthetic data. Instead, its purpose is to test the robustness of the strategy. We accomplish this by using a sequence of overlapping in-sample and out-of-sample periods to evaluate how well the strategy stands up, assuming the parameters are optimized on in-sample periods of varying size and start date and tested of similarly varying out-of-sample periods. A strategy that fails a cluster of such tests is unlikely to prove robust in live trading. A strategy that passes a test cluster at least demonstrates some capability to perform well in different market regimes.
To some extent we might regard such a test as unnecessary, given that the strategy has already been observed to perform well under several different market conditions, encapsulated in the different synthetic price series, in addition to the real historical price series. Nonetheless, we conduct a WFO cluster test to further evaluate the robustness of the strategy.
As the goal of the procedure is not to maximize the theoretical profitability of the strategy, but rather to evaluate its robustness, we select a criterion other than net profit as the factor to optimize. Specifically, we select the sum of the areas of the strategy drawdowns as the quantity to minimize (by maximizing the inverse of the sum of drawdown areas, which amounts to the same thing). This requires a little explanation.
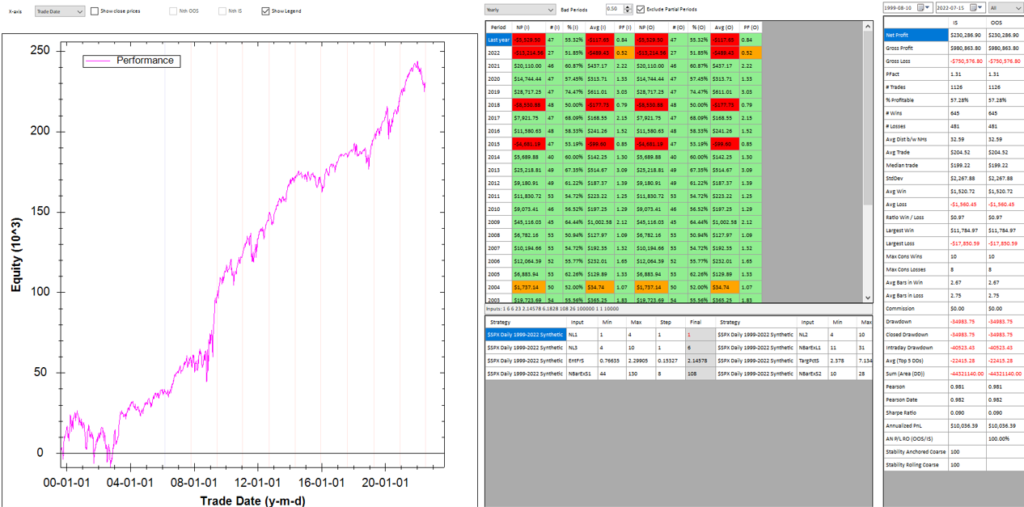
If we look at the strategy drawdown periods of the equity curve, we observe several periods (highlighted in red) in which the strategy was underwater:
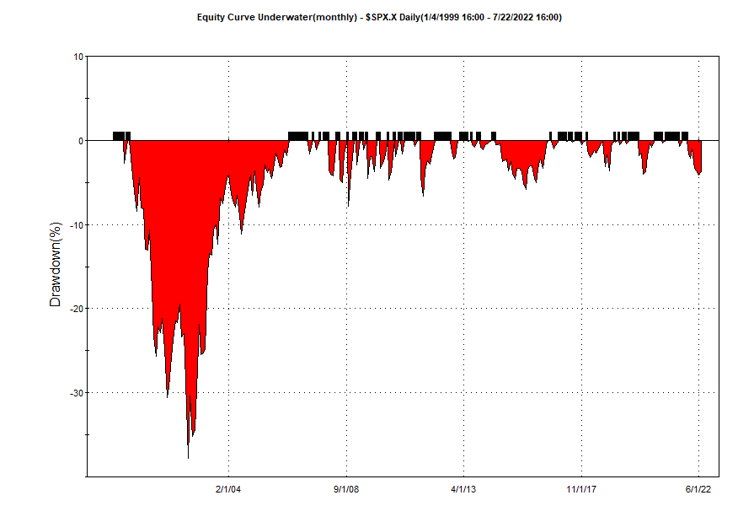
The area of each drawdown represents the length and magnitude of the drawdown and our goal here is to minimize the sum of these areas, so that we reduce both the total duration and severity of strategy drawdowns.
In each WFO test we use different % of OOS data and a different number of runs, assessing the performance of the strategy on a battery of different criteria:
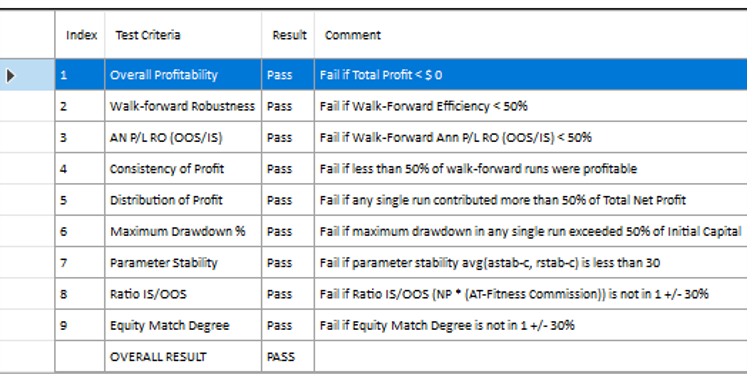
These criteria not only include overall profitability, but also factors such as parameter stability, profit consistency in each test, the ratio of in-sample to out-of-sample profits, etc. In other words, this WFO cluster analysis is not about profit maximization, but robustness evaluation, as assessed by these several different metrics. And in this case the strategy passes every test with flying colors:
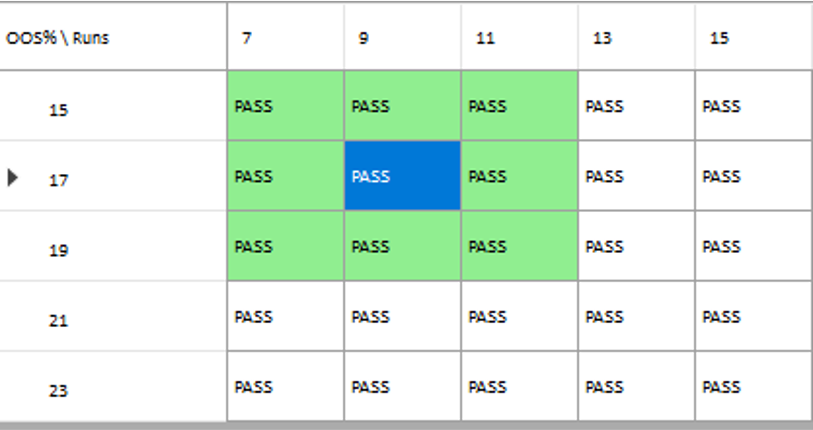
Other than validating the robustness of the strategy’s performance, the overall effect of the procedure is to slightly improve the equity curve by diminishing the magnitude and duration of the drawdown periods:
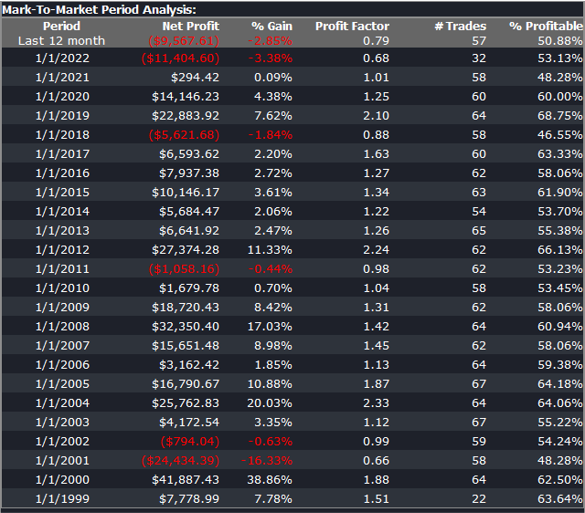
Conclusion
We have shown how, by using synthetic price series, we can build a robust trading strategy that performs well under a variety of different market conditions, including on previously “unseen” historical market data. Further analysis using cluster WFO tests strengthens the assessment of the strategy’s robustness.
A New Approach to Generating Synthetic Market Data
The Importance of Synthetic Market Data
The principal argument in favor of using synthetic data is that it addresses one of the major concerns about using real data series for modelling purposes: i.e. that models designed to fit the historical data produce test results that are unlikely to be replicated, going forward. Such models are not robust to changes that are likely to occur in any dynamical statistical process and will consequently perform poorly out of sample.
By using multiple synthetic data series following a wide range of different price paths, one can hope to build models – both for risk management and investment purposes – that can accommodate a variety of different market scenarios, making them more likely to perform robustly in a live market context.
Producing authentic synthetic data is a significant challenge, one that has eluded researchers for many years. Generating artificial returns series is a considerably simpler task, but even here there are difficulties. For many applications it is simply not sufficient to sample from the empirical distribution, because we want to produce a sequence of returns that closely mirrors the pattern of real returns sequences. In particular, there may be long memory effects (non-zero autocorrelations at long lags) or GARCH effects, in which dependency is introduced into the returns process via the square (or absolute value) of returns. These have the effect of inducing “shocks” to the returns process that persist for some time, causing autocorrelation in the associated volatility process in the process.
But producing a set of synthetic stock price data is even more of a challenge because not only do the above do the above requirements apply, but we also need to ensure that the open, high, low and closing prices are internally consistent, i.e. that on any given bar the High >= {Open, Low and Close) and that the Low <= {Open, Close}. These basic consistency checks have been overlooked in the research thus far.
Econometric Methods
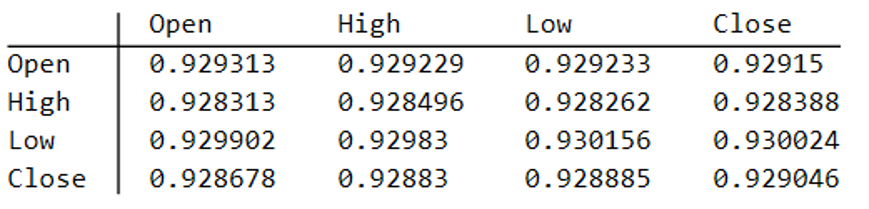
One classical approach to the problem would be to create a Vector Autoregression Model, in which lagged values of the Open, High, Low and Close prices are used to predict the current values (see here for a detailed exposition of the VAR approach). A compelling argument in favor of such models is that, almost by definition, O/H/L/C prices are necessarily cointegrated.
While a VAR model potentially has the ability to model long memory and even GARCH effects, it is unable to produce stock prices that are guaranteed to be consistent, in the sense defined above. Indeed, a failure rate of 35% or higher for basic consistency checks is typical for such a model, making the usefulness of the synthetic prices series highly questionable.
Another approach favored by some researchers is to stitch together sub-samples of the real data series in a varying time-order. This is applicable only to return series and, in any case, can introduce spurious autocorrelations, or overlook important dependencies in the data series. Besides these defects, it is challenging to produce a synthetic series that looks substantially different from the original – both the real and synthetic series exhibit common peaks and troughs, even if they occur in different places in each series.
Deep Learning Generative Adversarial Networks
In a previous post I looked in some detail at TimeGAN, one of the more recent methods for producing synthetic data series introduced in a paper in 2019 by Yoon, et al (link here).
TimeGAN, which applies deep learning Generative Adversarial Networks to create synthetic data series, appears to work quite well for certain types of time series. But in my research I found it be inadequate for the purpose of producing synthetic stock data, for three reasons:
(i) The model produces synthetic data of fixed window lengths and stitching these together to form a single series can be problematic.
(ii) The prices fail a significant percentage of the basic consistency tests, regardless of the number of epochs used to train the model
(iii) The methodology introduces spurious correlations in the associated returns process that do not correspond to anything found in real stock return series and which get more pronounced as training continues.
Another GAN model, DoppleGANger, introduced by Lin, et. al. in 2020 (paper here) seeks to improve on TimeGAN and claims “up to 43% better fidelity than baseline models”, including TimeGAN. However, in my research I found that, while DoppleGANger trains much more quickly than TimeGAN, it produces a consistency test failure rate exceeding 30%, even after training for 500,000 epochs.
For both TimeGAN and DoppleGANger, the researchers have tended to benchmark performance using classical data science metrics such as TSNE plots rather than the more prosaic consistency checks that a market data specialist would be interested in, while the more advanced requirements such as long memory and GARCH effects are passed by without a mention.
The conclusion is that current methods fail to provide an adequate means of generating synthetic price series for financial assets that are consistent and sufficiently representative to be practically useful.
The Ideal Algorithm for Producing Synthetic Data Series
What are we looking for in the ideal algorithm for generating stock prices? The list would include:
(i) Computational simplicity & efficiency. Important if we are looking to mass-produce synthetic series for a large number of assets, for a variety of different applications. Some deep learning methods would struggle to meet this requirement, even supposing that transfer learning is possible.
(ii) The ability to produce price series that are internally consistent (i.e High > Low, etc) in every case .
(iii) Should be able to produce a range of synthetic series that vary widely in their correspondence to the original price series. In some case we want synthetic price series that are highly correlated to the original; in other cases we might want to test our investment portfolio or risk control systems under extreme conditions never before seen in the market.
(iv) The distribution of returns in the synthetic series should closely match the historical series, being non-Gaussian and with “fat-tails”.
(v) The ability to incorporate long memory effects in the sequence of returns.
(vi) The ability to model GARCH effects in the returns process.
After researching the problem over the course of many years, I have at last succeeded in developing an algorithm that meets these requirements. Before delving into the mechanics, let me begin by illustrating its application.
Application of the Ideal Algorithm
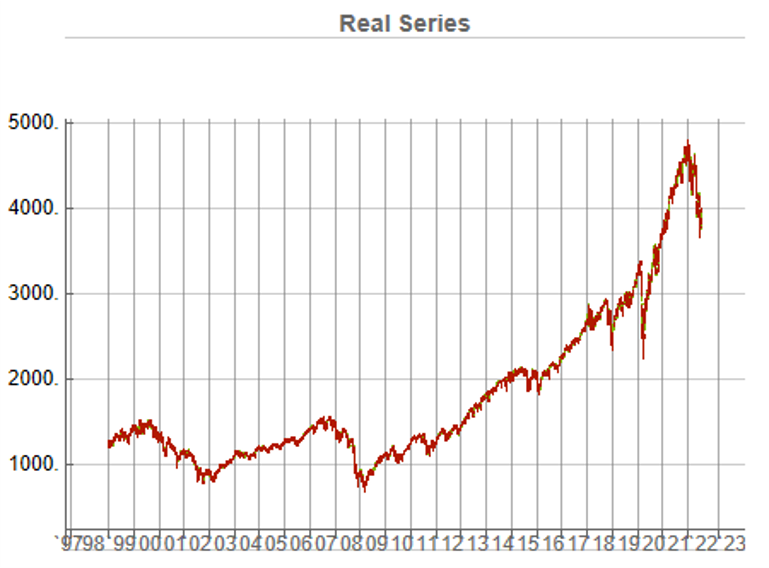
In this demonstration I am using daily O/H/L/C prices for the S&P 500 index for the period from Jan 1999 to July 2022, comprising four price series over 5,297 daily periods.

Synthetic Price Series
Generating ten synthetic series using the algorithm takes around 2 seconds with parallelization. I chose to generate series of the same length as the original, although I could just as easily have produced shorter, or longer sequences.
The first task is to confirm that the synthetic data are internally consistent, and indeed is guaranteed to be so because of the way the algorithm is designed. For example, here are the first few daily bars from the first synthetic series:
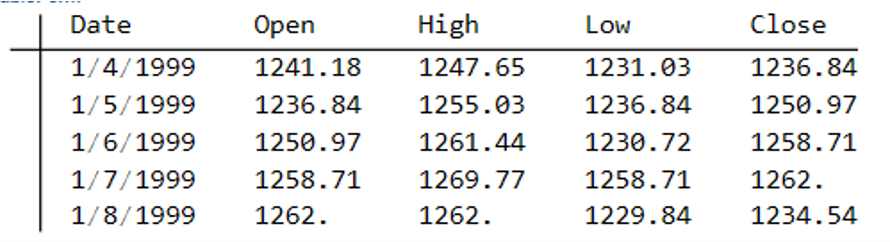
This means, of course, that we can immediately plot the synthetic series in a candlestick chart, just as we did with the real data series, above.
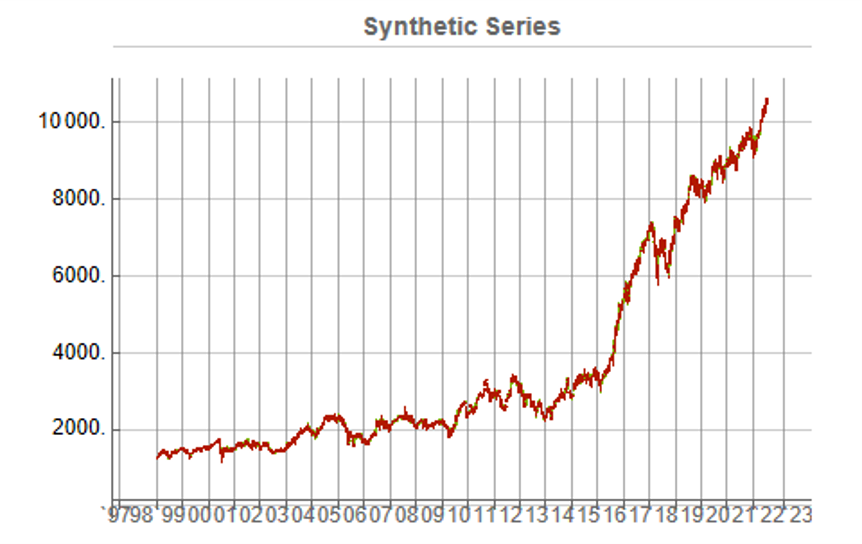
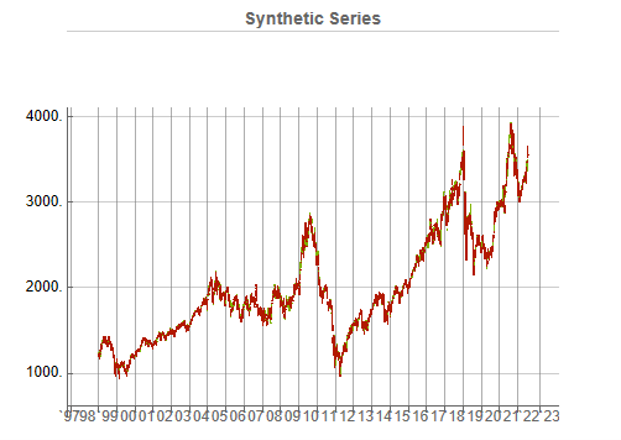
While the real and synthetic series are clearly different, the pattern of peaks and troughs somehow looks recognizably familiar. So, too, is the upward drift in the series, which is this case carries the synthetic S&P 500 Index to a high above 10,000 in 2022. Obviously this is a much more bullish scenario that we have seen in reality. But in fact this is just one example taken from the more “optimistic” end of the spectrum of possibilities. An illustration from the opposite end of the spectrum is shown in the chart below, in which the Index moves sideways over the entire 23 year span, with several very large drawdowns of -20% or more:
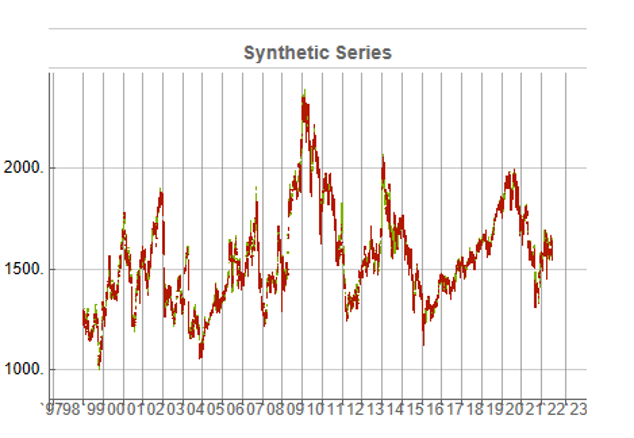
A more typical scenario might look something like our third chart, below. Here, too, we see several very large drawdowns, especially in the period from 2010-2011, but there is also a general upward drift in the process that enables the Index to reach levels comparable to those achieved by the real series:

Price Correlations
Reflecting these very different price path evolutions, we observe large variation in the correlations between the real and synthetic price series. For example:
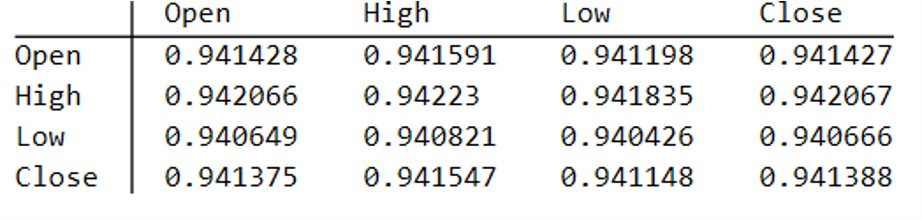
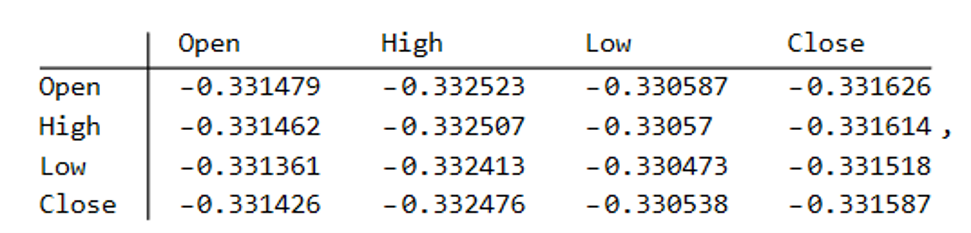
As these tables indicate, the algorithm is capable of producing replica series that either mimic the original, real price series very closely, or which show completely different behavior, as in the second example.
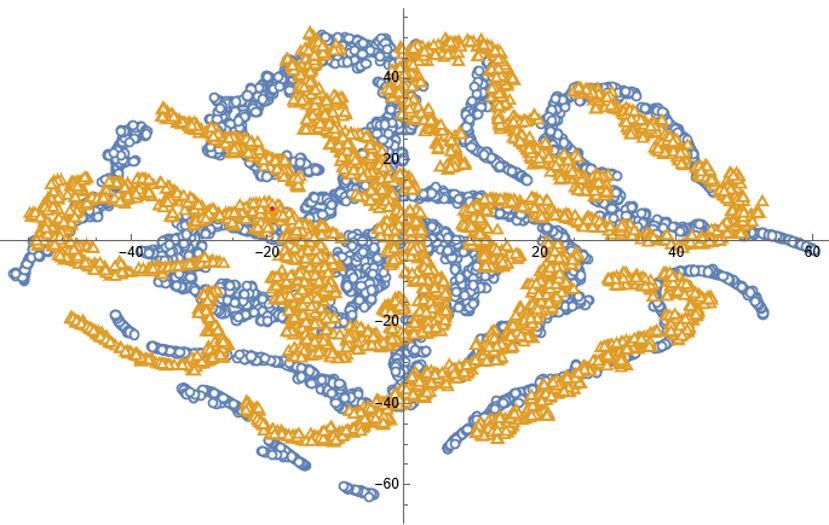
Dimensionality Reduction
For completeness, as have previous researchers, we apply t-SNE dimensionality reduction and plot the two-factor weightings for both real (yellow) and synthetic data (blue). We observe that while there is considerable overlap in reduced dimensional space, it is not as pronounced as for the synthetic data produced by TimeGAN, for instance. However, as previously explained, we are less concerned by this than we are about the tests previously described, which in our view provide a more appropriate analysis benchmark, so far as market data is concerned. Furthermore, for the reasons previously given, we want synthetic market data that in some cases tracks well beyond the range seen in historical price series.
Returns Distributions
Moving on, we next consider the characteristics of the returns in the synthetic series in comparison to the real data series, where returns are measured as the differences in the Log-Close prices, in the usual way.
Histograms of the returns for the most “optimistic” and “pessimistic” scenarios charted previously are shown below:
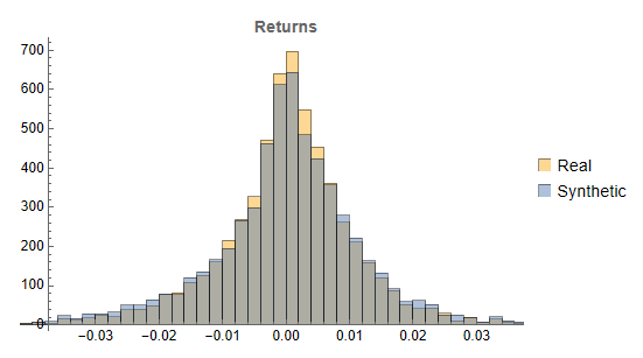
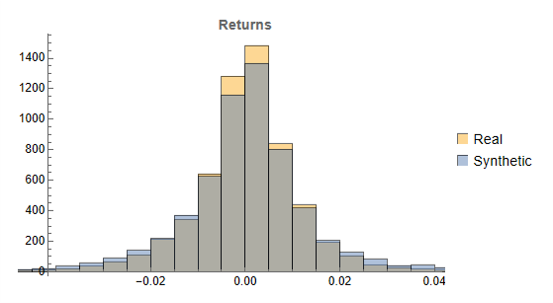
In both cases the distribution of returns in the synthetic series closely matches that of the real returns process and are clearly non-Gaussian, with an over-weighting in the distribution tails. A more detailed look at the distribution characteristics for the first four synthetic series indicates that there is a very good match to the real returns process in each case (the results for other series are very similar):
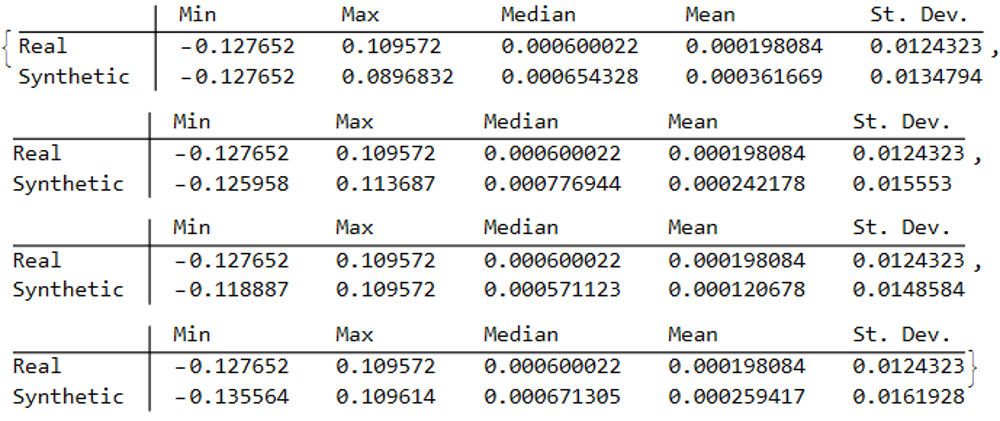
We observe that the minimum and maximum returns of the synthetic series sometimes exceed those of the real series, which can be a useful characteristic for risk management applications. The median and mean of the real and synthetic series are broadly similar, sometimes higher, in other cases lower. Only for the standard deviation of returns do we observe a systematic pattern, in which returns volatility in the synthetic series is consistently higher than in the real series.
This feature, I would argue, is both appropriate and useful. Standard deviations should generally be higher, because there is indeed greater uncertainty about the prices and returns in artificially generated synthetic data, compared to the real series. Moreover, this characteristic is useful, because it will impose a greater stress-test burden on risk management systems compared to simply drawing from the distribution of real returns using Monte Carlo simulation. Put simply, there will be a greater number of more extreme tail events in scenarios using synthetic data, and this will cause risk control parameters to be set more conservatively than they otherwise might. This same characteristic – the greater variation in prices and returns – will also pose a tougher challenge for AI systems that attempt to create trading strategies using genetic programming, meaning that any such strategies are more likely to perform robustly in a live trading environment. I will be returning to this issue in a follow-up post.
Returns Process Characteristics
In the following plot we take a look at the autocorrelations in the returns process for a typical synthetic series. These compare closely with the autocorrelations in the real returns series up to 50 lags, which means that any long memory effects are likely to be conserved.
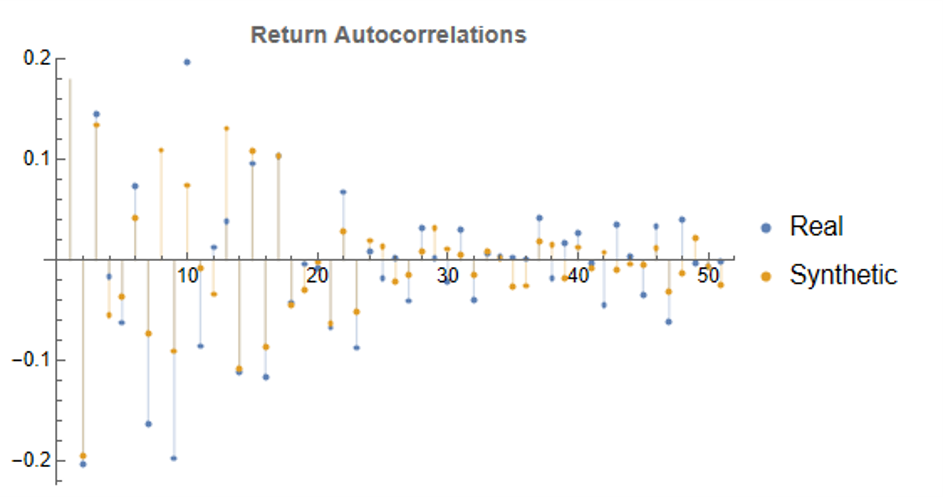
Finally, when we come to consider the autocorrelations in the square of the returns, we observe slowly decaying coefficients over long lags – evidence of so-called GARCH effects – for both real and synthetic series:
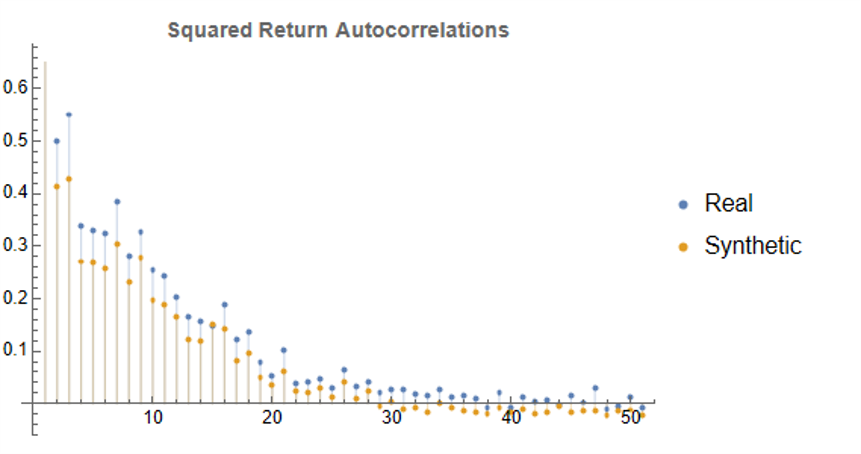
Summary
Overall, we observe that the algorithm is capable of generating consistent stock price series that correlate highly with the real price series. It is also capable of generating price series that have low, or even negative, correlation, a feature that may have important applications in the context of risk management. The distribution of returns in the synthetic series closely match those of the real returns process, and moreover retain important features such as long memory and GARCH effects.
Objections to the Use of Synthetic Data
Criticism of synthetic market data (including from myself) has hitherto focused on the inadequacy of such data in terms of representing important characteristics of real data series. Now that such technical issues have been addressed, I will try to anticipate some of the additional concerns that are likely to surface, going forward.
- The Synthetic Data is “Unrealistic”
What is meant here is that there is no plausible set of real, economic factors that would be likely to combine in a way to produce the pattern of prices shown in some of the synthetic data series. The idea that, as observed in one of the artificial scenarios above, the Fed would stand idly by while the market plunged by 50% to 60%, seems highly implausible. Equally unlikely is a scenario in which the market moves sideways for an extended period of a decade, or longer.
To a limited extent, I would agree with this. However, just because such scenarios are currently unlikely doesn’t mean they can never happen. For instance, take a look at the performance of the S&P 500 Index over the period from 1966 through 1979:
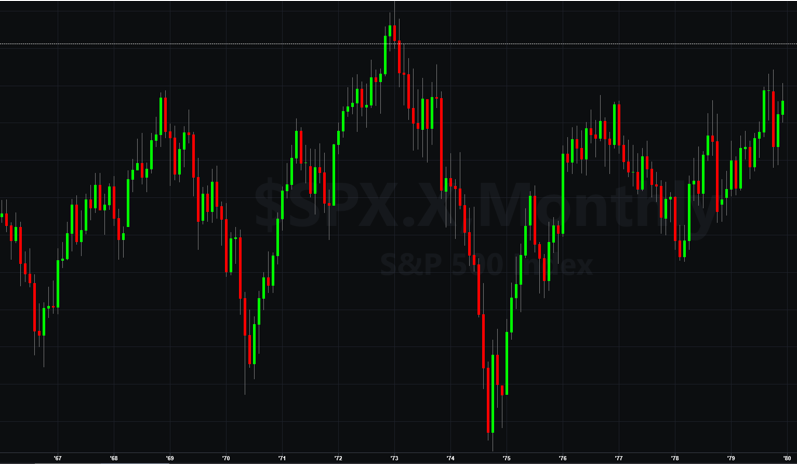
The market index barely made any progress throughout the entire 13-year period, which was characterized by a vicious bout of stagflation. Note, too, the precipitous drop in the index following the oil shock in 1973.
So to say that such scenarios – however implausible they may appear to be – can never happen is simply mistaken.
Finally, let’s not forget that, while the focus of this article is on the US market index, there are many economies, such as Mexico, Brazil or Argentina, for which such adverse developments are much more credible than they might currently be for the United States. We may wish to produce synthetic data for the markets in such economies for modelling purposes, in which case we will want to generate synthetic data capturing the full range of possible market outcomes, including some of the worst-case scenarios.
2. Extreme Scenarios Occur Too Frequently in Synthetic Data
Actually this is not the case – the generator tends to produce extreme scenarios with a frequency that is plausible, given the history and characteristics of the underlying, real price process. But there can be good reasons for wanting to control the frequency of such scenarios.
For instance, an investment manager may be looking to develop a “long-only” investment portfolio because, given his investment remit, that is the only type of investment strategy permitted. He would likely want to limit his focus to the more benign market outcomes for two reasons: (i) his investment thesis is that the market is likely to perform well, going forward (or else how does he pitch his strategy to investors?) and (ii) while he accepts that he may be wrong, it is not his job to hedge a possible market downturn – the responsibility for dealing with an adverse outcome falls to his risk manager, or to the investor.
Conversely, a risk manager is much more likely to be interested in adverse scenarios and, if anything, is likely to want to see such outcomes over-represented in a sample of synthetic data.
The point is, there is no “correct” answer: one has to decide which types of scenarios best suit the application one has in mind and sample the data accordingly. This can be done in a variety of ways such as setting a minimum required correlation between the synthetic and real price series, or designing a system of stratified sampling in which the desired outcomes are sampled according to a stipulated frequency distribution.
3. Synthetic Data Does Not Prevent Data Snooping and Curve Fitting
A critic might argue that, in fact, the real market data is “unseen” only in a theoretical sense, since its essential attributes have been baked into the synthetic series produced by the generator. This applies to an even greater extent if the synthetic series are sampled in some way, as described above.
I think this is a fair point. To take an extreme scenario, one could choose to select only synthetic series for which the correlation with the real data is 99.9%, or higher. Clearly this runs counter to the spirit of what one is trying to achieve with synthetic data and one might just as well use real data for modelling purposes. In practice, of course, even where a sampling methodology is applied, it is unlikely to be as crudely biased as in this example.
But, in any case, what is the alternative? The only option I can see is one in which a pure mathematical model is used to produce synthetic data, without any reference to the underlying real series. But, in that case, how would one assess the validity of the model assumptions, or how representative the synthetic series it produces might be?
There is no alternative but to have recourse to the real data at some point in the modelling process. In this procedure, however, the impact of snooping bias or curve fitting, even though it can never be totally extinguished, is very much diminished and it plays a less central role in model development.
Conclusion
It is now possible to produce synthetic data series that have all of the hallmark characteristics of real price data. This permits the analyst to investigate market models without direct recourse to the real price series, thereby minimizing data snooping and curve fitting bias. Models developed using synthetic data describing many different price path evolutions are more likely to prove robust across a wider range of plausible market scenarios in the real world.
In the next, follow-up post I will illustrate the application of synthetic data to the development of a robust investment strategy.
Generating Synthetic Market Data
Why Synthetic Data?
Synthetic market data has great potential for applications in financial research. Examples include testing the risk characteristics of a trading book or investment portfolio, developing trading strategies using previously unseen data, or simulating high frequency trading activity in a limit order book. It provides an answer to the criticism of curve fitting that is routinely levelled at existing approaches that use the single, observed historical path followed by an asset to construct investment and risk models. Such models, critics argue, are usually over-fitted to the historical data and are consequently unlikely to prove robust, going forward.
What is required is a model of the underlying asset processes that can then be used to generate a large number of price paths for all of the constituents of an investment portfolio. This should provide a more realistic assessment of the range of possible behaviours of the portfolio under a wide variety of market conditions, including during tail events.
Existing Methodology
Current approaches to modelling asset processes are often rudimentary and fail to capture the interplay of market dynamics that impact the evolution of the process. So, for example, we might begin by modelling the process of asset returns using a Gaussian or Student-T distribution. This immediately runs into the issue of under-representing the “fat tails” of empirical asset distributions, where tail events occur much more frequently than standard distributions would suggest. We might move on consider using the empirical distribution itself, and this might be sufficient for some applications.
But in many cases we want to generate a sequence of returns, or perhaps a time series of Open/High/Low/Close prices for modelling purposes. This is a challenge that is at least an order of magnitude more difficult. We not only have to ensure that the returns and/or prices at each individual time step are consistent (e.g. that the High > Low, in the case of prices, for example), but also that the sequence of returns is representative of known characteristics of financial assets such as serial autocorrelation, cross correlation and volatility clustering. GARCH models serve reasonably well in this context, but, for example, fail to capture long memory effects, amongst other deficiencies.
Deep Learning Models
Generative Adversarial Networks have become ubiquitous in the generation of “deep fakes” – .synthesised images generated by deep learning models that are close to indistinguishable from the real thing, whether it be the image of a human face, or medical images such X-ray scans. In 2019 Jinsung Yoon, Daniel Jarrett, and Mihaela van der Schaar published a paper on Time-series Generative Adversarial Networks (“TimeGAN”) in Neural Information Processing Systems (link to paper here) , a deep learning model that can be used to generate synthetic time series data.
An important characteristic of time series data is that it extends regular tabular data in the third dimension (i.e time):
As the authors note:
“A good generative model for time-series data should preserve temporal dynamics, in the sense that new sequences respect the original relationships between variables across time. Existing methods that bring generative adversarial networks (GANs) into the sequential setting do not adequately attend to the temporal correlations unique to time-series data. At the same time, supervised models for sequence prediction – which allow finer control over network dynamics – are inherently deterministic.”
They continue:
“[TimeGAN is a] novel framework for generating realistic time-series data that combines the flexibility of the unsupervised paradigm with the control afforded by supervised training. Through a learned embedding space jointly optimized with both supervised and adversarial objectives, we encourage the network to adhere to the dynamics of the training data during sampling”.
This sounds very promising and indeed the authors claim that “Qualitatively and quantitatively, we find that the proposed framework consistently and significantly outperforms state-of-the-art benchmarks with respect to measures of similarity and predictive ability” for several different types of time series dataset, including stock data.
A Brief Interlude on Generative Adversarial Networks
In the GAN architecture we implement two models: one to generate artificial data and another to distinguish artificial from real data. For example, a GAN model to generate artificial images of handwritten numbers would look approximately like this:
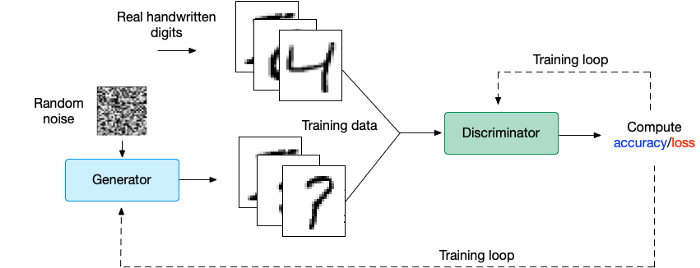
There are many architectures to consider for building the discriminator and the generator. We could build a deep neural network or Convolutional Neural Network (CNN) as well as other options.
TimeGAN
In the context of time series we face not only the problem of matching the features of synthetic and real data sequences, but also calibrating the time dynamics of the underlying generation process. TimeGAN addresses these challenges by using an unsupervised adversarial loss on both real and synthetic sequences, coupled with a stepwise supervised loss using the original data as supervision, thereby explicitly encouraging the model to capture the stepwise conditional distributions in the data. This takes advantage of the fact that there is more information in the training data than simply whether each datum is real or synthetic; we can expressly learn from the transition dynamics from real sequences.
A further innovative feature of the TimeGAN model in the introduction of an embedding network to provide a reversible mapping between features and latent representations, thereby reducing the high-dimensionality of the adversarial learning space. This capitalizes on the fact the temporal dynamics of even complex systems are often driven by fewer and lower-dimensional factors of variation.
Importantly, the supervised loss is minimized by jointly training both the embedding and generator networks, such that the latent space not only serves to promote parameter efficiency—it is specifically conditioned to facilitate the generator in learning temporal relationships.
The figure below shows how the various components are arranged and how the information flows between them during training in TimeGAN.
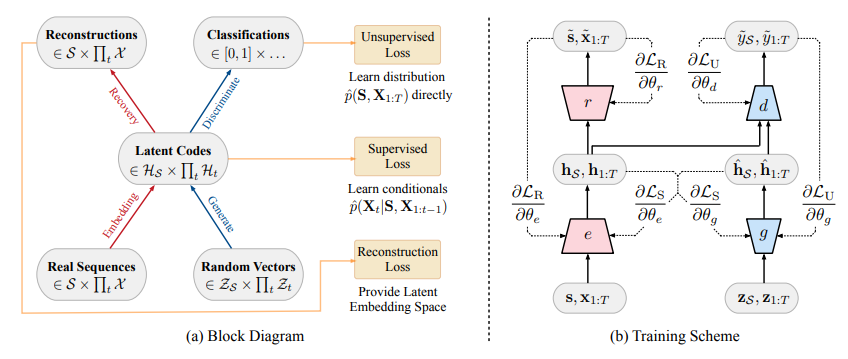
Further details of the TimeGAN model can be found in the paper and in the accompanying GitHub repository, which is found here.
Evaluating the Performance of TimeGAN
The researchers test the TimeGAN methodology using several different datasets, such as daily stock data for the period 2004 to 2019 downloaded from Google, including as features the volume and high, low, opening, and closing prices.
The TimeGAN model is trained for 50,000 epochs with a batch size of 128, using a 24-period rolling window, which the authors found to be the optimal window size. The trained synthesizer produces samples comprising a (128 x 24 x 5) dataframe of price and volume data which can then be compared to the original stock series. It is worth noting that the starting prices of each 24-period window are generated independently, meaning that, for example, the opening price in one sample window might be 10x larger than in another window. This immediately indicates one of the drawbacks of the TimeGAN approach: i.e. that the window length of the generated data is fixed and it can be challenging to stitch windows together to create a longer synthetic series, given that the initial prices for each vary considerably from window to window.
The data visualization methods chosen by the authors to evaluate the performance of the synthetic series in reproducing the features of the original series is problematic, at least as far as stock data is concerned. Both TSNE and PCA plots of the real vs. synthetic data appear to indicate a very close match:
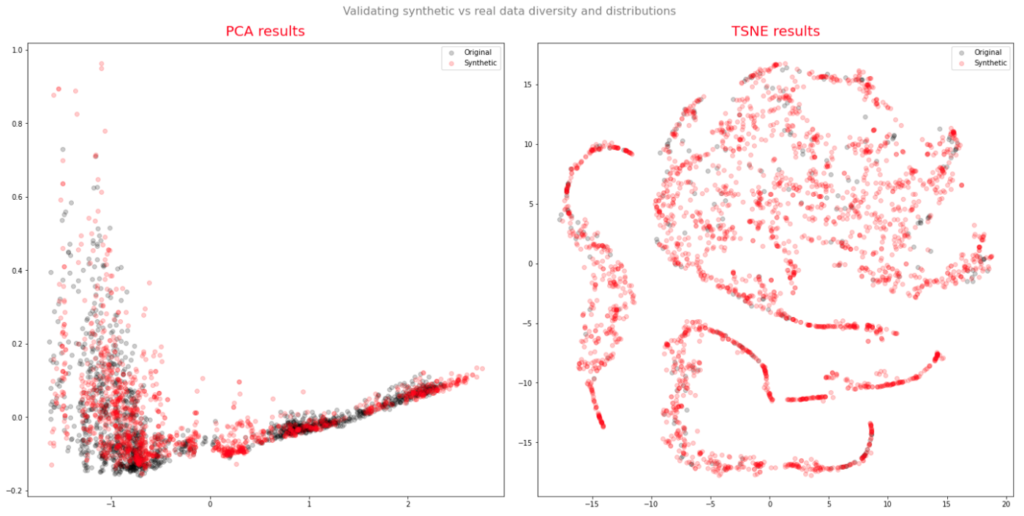
This illustrates how misleading it can be to rely on data visualization for inference purposes. For stock data, there are some very basic tests that should first be performed to ensure the consistency of the synthetic output. In particular, in each row of the window, the High should exceed the Open, Low and Close prices, with the Low price falling below the Open, High and Close prices.
In my experimentation I found that after training the model for 50,000 epochs, the synthetic data failed these basic tests in around 15% of the sample. Further training rounds up to 100,000 epochs reduced the error rate to only 5% and it should be possible to eliminate almost all of these basic data issues with further rounds of training.
However, another basic problem with the synthetic data rapidly becomes apparent: the period to period (in this case, daily) returns have a strong tendency to diminish over time, typically being an order of magnitude larger at the start of each window than towards the end. This pattern of behavior is bound to introduce spurious autocorrelation and volatility-decay effects that are nowhere to be found in the real data series.
Finally, the fixed, limited window size and the independence of each window sample of synthetic data make it impossible to account for important characteristics such as volatility clustering or long memory effects in any adequate way.
Taken together, these flaws render the synthetic stock data produced by TimeGAN significantly unrepresentative and highly unreliable for modelling purposes.
Conclusion
TimeGAN is an important innovation in the field of synthetic data generation, with particular relevance to time series data. However it has significant limitations that make its application to financial time series problematic, in regard to the fixed window length, inconsistencies in the price data and spurious autocorrelation in the returns of the synthetic series it generates.