Posts

Posted on

The Hedged Volatility Strategy

Being short regular Volatility ETFs or long Inverse Volatility ETFs are winning strategies…most of the time. The challenge is that when the VIX spikes or when the VIX futures curve is downward sloping instead of upward sloping, very significant losses can occur. Many people have built and back-tested models that attempt to move from long to short to neutral positions in the various Volatility ETFs, but almost all of them have one or both of these very significant flaws: 1) Failure to use “out of sample” back-testing and 2) Failure to protect against “black swan” events.

In this strategy a position and weighting in the appropriate Volatility ETFs are established based on a multi-factor model which always uses out of sample back-testing to determine effectiveness. Volatility Options are always used to protect against significant short-term moves which left unchecked could result in the total loss of one’s portfolio value; these options will usually lose money, but that is a small price to pay for the protection they provide. (Strategies should be scaled at a minimum of 20% to ensure options protection.)

This is a good strategy for IRA accounts in which short selling is not allowed. Long positions in Inverse Volatility ETFs are typically held. Suggested minimum capital: $26,000 (using 20% scaling).

Posted on

Can Machine Learning Techniques Be Used To Predict Market Direction? The 1,000,000 Model Test.

During the 1990’s the advent of Neural Networks unleashed a torrent of research on their applications in financial markets, accompanied by some rather extravagant claims about their predicative abilities.  Sadly, much of the research proved to be sub-standard and the results illusionary, following which the topic was largely relegated to the bleachers, at least in the field of financial market research.

With the advent of new machine learning techniques such as Random Forests, Support Vector Machines and Nearest Neighbor Classification, there has been a resurgence of interest in non-linear modeling techniques and a flood of new research, a fair amount of it supportive of their potential for forecasting financial markets.  Once again, however, doubts about the quality of some of the research bring the results into question.

SSALGOTRADING AD

Against this background I and my co-researcher Dan Rico set out to address the question of whether these new techniques really do have predicative power, more specifically the ability to forecast market direction.  Using some excellent MatLab toolboxes and a new software package, an Excel Addin called 11Ants, that makes large scale testing of multiple models a snap, we examined over 1,000,000 models and model-ensembles, covering just about every available non-linear technique.  The data set for our study comprised daily prices for a selection of US equity securities, together with a large selection of technical indicators for which some other researchers have claimed explanatory power.

In-Sample Equity Curve for Best Performing Nonlinear Model
In-Sample Equity Curve for Best Performing Nonlinear Model

The answer provided by our research was, without exception, in the negative: not one of the models tested showed any significant ability to predict the direction of any of the securities in our data set.  Furthermore, our study found that the best-performing models favored raw price data over technical indicator variables, suggesting that the latter have little explanatory power.

As with Neural Networks, the principal difficulty with non-linear techniques appears to be curve-fitting and a failure to generalize:  while it is very easy to find models that provide an excellent fit to in-sample data, the forecasting performance out-of-sample is often very poor.

Out-of-Sample Equity Curve for Best Performing Nonlinear Model
Out-of-Sample Equity Curve for Best Performing Nonlinear Model

Some caveats about our own research apply.  First and foremost, it is of course impossible to prove a hypothesis in the negative.  Secondly, it is plausible that some markets are less efficient than others:  some studies have claimed success in developing predictive models due to the (relative) inefficiency of the F/X and futures markets, for example.  Thirdly, the choice of sample period may be criticized:  it could be that the models were over-conditioned on a too- lengthy in-sample data set, which in one case ran from 1993 to 2008, with just two years (2009-2010) of out-of-sample data.  The choice of sample was deliberate, however:  had we omitted the 2008 period from the “learning” data set, it would be very easy to criticize the study for failing to allow the algorithms to learn about the exceptional behavior of the markets during that turbulent year.

Despite these limitations, our research casts doubt on the findings of some less-extensive studies, that may be the result of sample-selection bias.  One characteristic of the most credible studies finding evidence in favor of market predictability, such as those by Pesaran and Timmermann, for instance (see paper for citations), is that the models they employ tend to incorporate independent explanatory variables, such as yield spreads, which do appear to have real explanatory power.  The finding of our study suggest that, absent such explanatory factors, the ability to predict markets using sophisticated non-linear techniques applied to price data alone may prove to be as illusionary as it was in the 1990’s.

 

ONE MILLION MODELS
Posted on

The F/X Momentum Strategy

Our approach is based upon the idea that currencies tend to be range bound, that momentum ultimately exhausts itself and that prices tend to fall faster than they rise. The strategy seeks to exploit these characteristics with short trades that may be closed within a few hours, or continue over several days when the exhaustion pattern emerges more slowly.
FXMomentum Aug 20 2018

Posted on

Covered Writes, Covered Wrongs

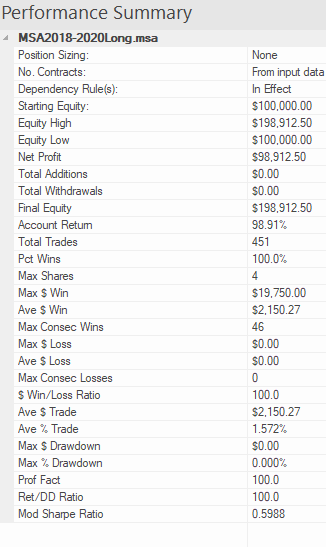
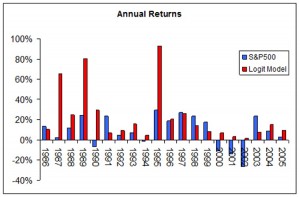
What is a Covered Call?

A covered call (or covered write or buy-write) is a long position in a security and a short position in a call option on that security.  The diagram below constructs the covered call payoff diagram, including the option premium, at expiration when the call option is written at a $100 strike with a $25 option premium.

Payoff

Equity index covered calls are an attractive strategy to many investors because they have realized returns not much lower than those of the equity market but with much lower volatility.  But investors often do the trade for the wrong reasons:  there are a number of myths about covered writes that persist even amongst professional options traders.  I have heard most, if not all of them professed by seasons floor traders on the American Stock Exchange and, I confess, I have even used one or two of them myself.  Roni Israelov and Larn Nielsen of AQR Capital Management, LLC have done a fine job of elucidating and then dispelling these misunderstandings about the strategy, in their paper Covered Call Strategies: One Fact and Eight Myths, Financial Analysts Journal, Vol. 70, No. 6, 2014.

SSALGOTRADING AD

The Cover Call Strategy and its Benefits for Investors

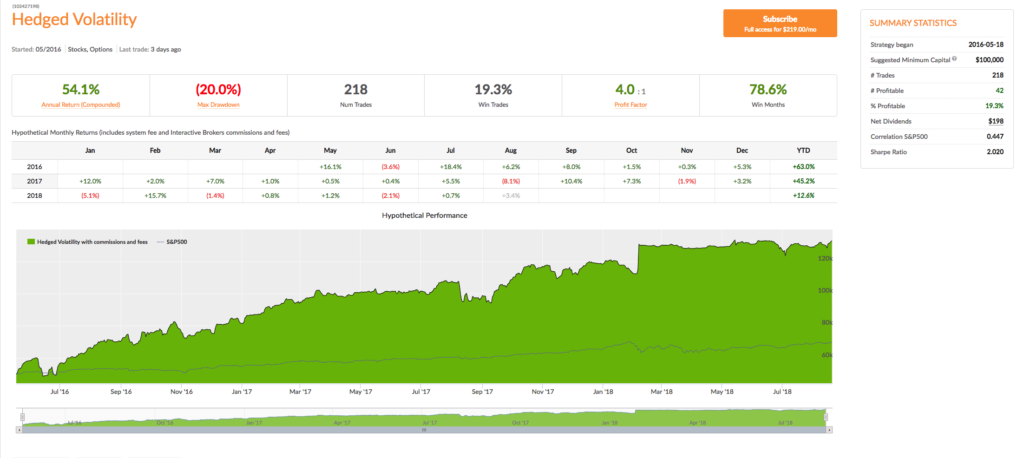
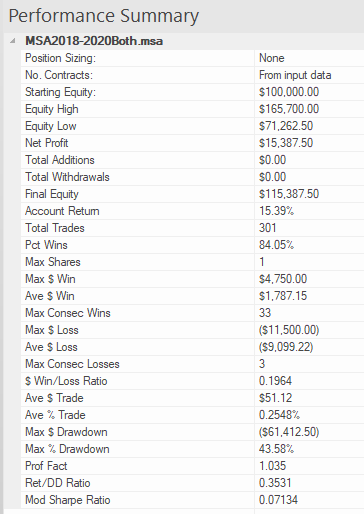
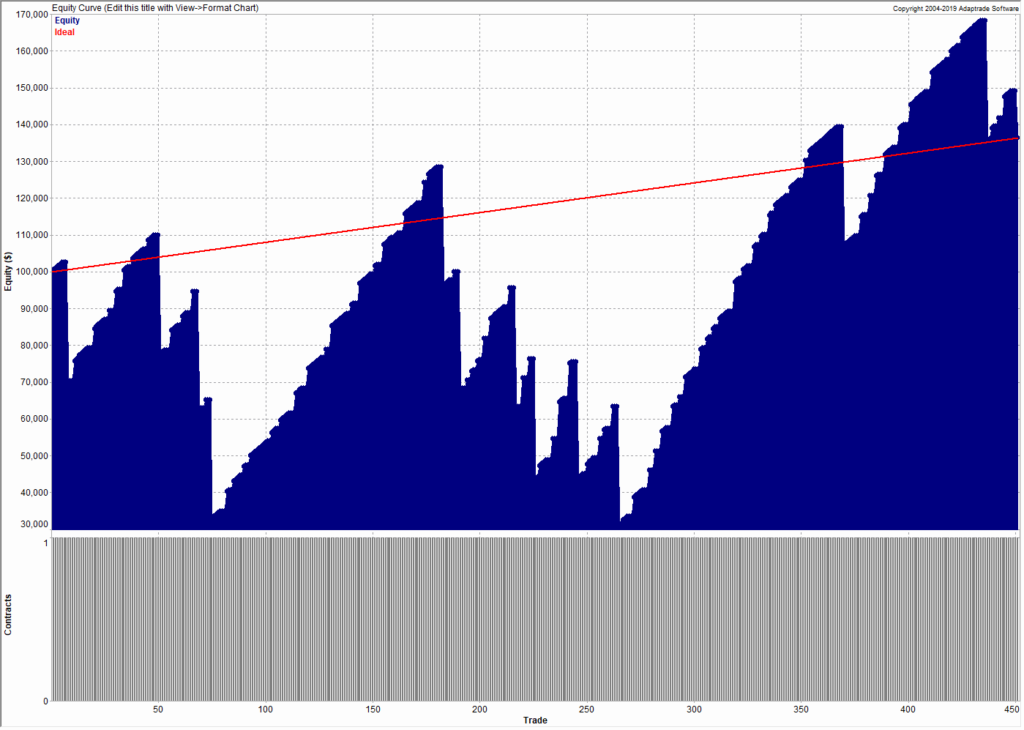
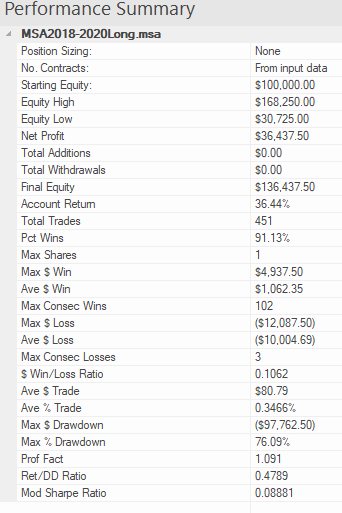
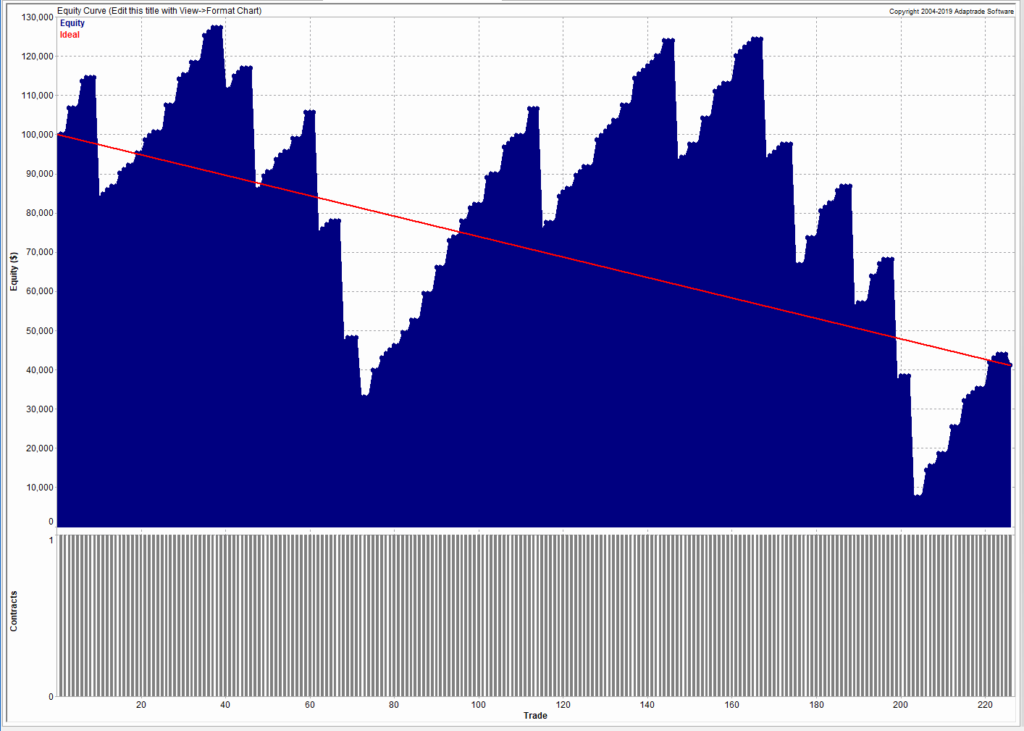
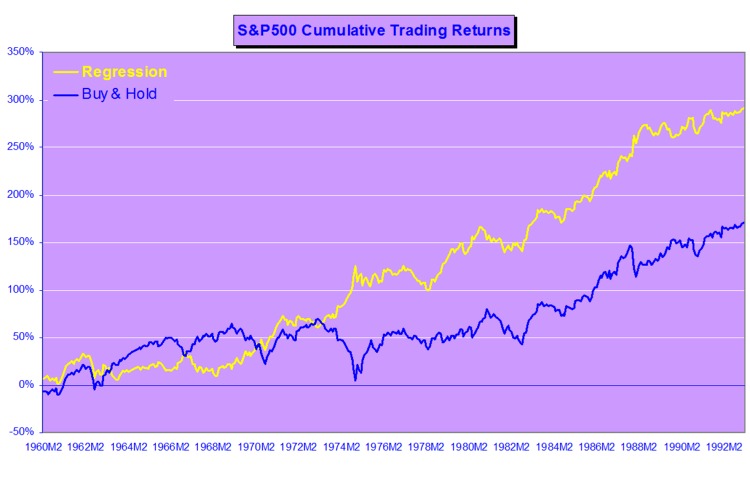
The covered call strategy has generated attention due to its attractive historical risk-adjusted returns. For example, the CBOE S&P 500 BuyWrite Index, the industry-standard covered call benchmark, is commonly described as providing average returns comparable to the S&P 500 Index with approximately two-thirds the volatility, supported by statistics such as those shown below.

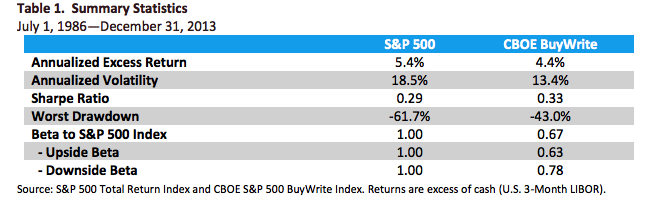
Table 1

The key advantages of the strategy (compared to an outright, delta-one position) include lower volatility, beta and tail risk.  As a consequence, the strategy produces higher risk-adjusted rates if return (Sharpe Ratio).  Note, too, the beta convexity of the strategy, a topic I cover in this post:

http://jonathankinlay.com/2017/05/beta-convexity/

Although the BuyWrite Index has historically demonstrated similar total returns to the S&P 500, it does so with a reduced beta to the S&P 500 Index. However, it is important to also understand that the BuyWrite Index is more exposed to negative S&P 500 returns than positive returns. This asymmetric relationship to the S&P 500 is consistent with its payoff characteristics and results from the fact that a covered call strategy sells optionality. What this means in simple terms is that while drawdowns are somewhat mitigated by the revenue associated with call writing, the upside is capped by those same call options.

Understandably, a strategy that produces equity-like return with lower beta and lower risk attracts considerable attention from investors.  According to Moringstar, growth in assets under management in covered call strategies has been over 25% per year over the 10 years through June 2014 with over $45 billion currently invested.

Myths about the Covered Call Strategy

Many option strategies are the subject of investor myths, partly, I suppose, because option strategies are relatively complicated and entail risks in several dimensions.  So it is quite easy for investors to become confused.  Simple anecdotes are attractive because they appear to cut through the complexity with an easily understood metaphor, but they can often be misleading.  An example is the widely-held view – even amongst professional option traders – is that selling volatility via strangles is a less risk approach than selling at-the-money straddles. Intuitively, this makes sense:  why wouldn’t  selling straddles that have strike prices (far) away from the current spot price be less risky than selling straddles that have strike prices close to the spot price?  But, in fact, it turns out that selling straddles is the less risky the two strategies – see this post for details:

http://jonathankinlay.com/2016/11/selling-volatility/

Likewise, the covered call strategy is subject to a number of “urban myths”, that turn out to be unfounded:

Myth 1: Risk exposure is described by the payoff diagram

That is only true at expiration.  Along the way, the positions will be marked-to-market and may produce a substantially different payoff if the trade is terminated early.  The same holds true for a zero-coupon bond – we know the terminal value for certain, but there can be considerable variation in the value of the asset from day to day.

Myth 2: Covered calls provide downside protection

This is partially true, but only in a very limited sense.  Unlike a long option hedge, the “protection” in a buy-write strategy is limited to only the premium collected on the option sale, a relatively modest amount in most cases.  Consider a covered call position on a $100 stock with a $10 at-the-money call premium. The covered call can potentially lose $90 and the long call option can lose $10. Each position has the same 50% exposure to the stock, but the covered call’s downside risk is disproportionate to its stock exposure. This is consistent with the covered call’s realized upside and downside betas as discussed earlier.

Myth 3: Covered calls generate income.

Remember that income is revenue minus costs.

It is true that option selling generates positive cash flow, but this incorrectly leads investors to the conclusion that covered calls generate investment income.  Just as is the case with bond issuance, the revenue generated from selling the call option is not income (though, like income, the cash flows received from selling options are considered taxable for many investors). In order for there to be investment income or earnings, the option must be sold at a favorable price – the option’s implied volatility needs to be higher than the stock’s expected volatility.

Myth 4: Covered calls on high-volatility stocks and/or shorter-dated options provide higher yield.

Though true that high volatility stocks and short-dated options command higher annualized premiums, insurance on riskier assets should rationally command a higher premium and selling insurance more often per year should provide higher annual premiums. However, these do not equate to higher net income or yield. For instance, if options are properly priced (e.g., according to the Black-Scholes pricing model), then selling 12 at-the-money options will generate approximately 3.5 times the cash flow of selling a single annual option, but this does not unequivocally translate into higher net profits as discussed earlier. Assuming fairly priced options, higher revenue is not necessarily a mechanism for increasing investment income.

The key point here is that what matters is value, not price. In other words, expected investment profits are generated by the option’s richness, not the option’s price. For example, if you want to short a stock with what you consider to be a high valuation, then the goal is not to find a stock with a high price, but rather one that is overpriced relative to its fundamental value. The same principle applies to options. It is not appropriate to seek an option with a high price or other characteristics associated with high prices. Investors must instead look for options that are expensive relative to their fundamental value.  Put another way, the investor should seek out options trading at a higher implied volatility than the likely futures realized volatility over the life of the option.

Myth 5: Time decay of options written works in your favor.

While it is true that the value of an option declines over time as it approaches expiration, that is not the whole story.  In fact an option’s expected intrinsic value increases as the underlying security realizes volatility.  What matters is whether the realized volatility turns out to be lower than the volatility baked into the option price – the implied volatility.  In truth, an option’s time decay only works in the seller’s favor if the option is initially priced expensive relative to its fundamental value. If the option is priced cheaply, then time decay works very much against the seller.

Myth 6: Covered calls are appropriate if you have a neutral to moderately bullish view.

This myth is an over-simplification.  In selling a call option you are expressing a view, not only on the future prospects for the stock, but also on its likely future volatility.  It is entirely possible that the stock could stall (or even decline) and yet the value of the option you have sold rises due, say, to takeover rumors.  A neutral view on the stock may imply a belief that the security price will not move far from its current price rather than its expected return is zero. If so, then a short straddle position is a way to express that view — not a covered call — because, in this case, no active position should be taken in the security.

Myth 7: Overwriting pays you for doing what you were going to do anyway

This myth is typically posed as the following question: if you have a price target for selling a stock you own, why not get paid to write a call option struck at that price target?

In fact this myth exposes the critical difference between a plan and a contractual obligation. If the former case, suppose that the stock hits your target price very much more quickly than you had anticipated, perhaps as a result of a new product announcement that you had not anticipated at the time you set your target.  In those circumstances you might very well choose to maintain your long position and revise your price target upwards. This is an example of a plan – a successful one – that can be adjusted to suit circumstances as they change.

A covered call strategy is an obligation, rather than a plan.  You have pre-sold the stock at the target price and, in the above scenario, you cannot change your mind in order to benefit from additional potential upside in the stock.

In other words, with a covered call strategy you have monetized the optionality that is inherent in any plan and turned it into a contractual obligation in exchange for a fee.

Myth 8: Overwriting allows you to buy a stock at a discounted price.

Here is how this myth is typically framed: if a stock that you would like to own is currently priced at $100 and that you think is currently expensive, you can act on that opinion by selling a naked put option at a $95 strike price and collect a premium of say $1. Then, if the price subsequently declines below the strike price, the option will likely be exercised thus requiring you to buy the stock for $95. Including the $1 premium, you effectively buy the stock at a 6% discount. If the option is not exercised you keep the premium as income. So, this type of outcome for selling naked put options may also lead you to conclude that the equivalent covered call strategy makes sense and is valuable.

But this argument is really a sleight of hand.  In our example above, if the option is exercised, then when you buy the stock for $95 you won’t care what the stock price was when you sold the option. What matters is the stock price on the date the option was exercised. If the stock price dropped all the way down to $80, the $95 purchase price no longer seems like a discount. Your P&L will show a mark-to-market loss of $14 ($95 – $80 – $1). The initial stock price is irrelevant and the $1 premium hardly helps.

Conclusion: How to Think About the Covered Call Strategy

Investors should ignore the misleading storytelling about obtaining downside buffers and generating income. A covered call strategy only generates income to the extent that any other strategy generates income, by buying or selling mispriced securities or securities with an embedded risk premium. Avoid the temptation to overly focus on payoff diagrams. If you believe the index will rise and implied volatilities are rich, a covered call is a step in the right direction towards expressing that view.

If you have no view on implied volatility, there is no reason to sell options, or covered calls

Aby znaleźć legalne kasyna online w Polsce, odwiedź stronę pl.kasynopolska10.com/legalne-kasyna/, partnera serwisu recenzującego kasyna online – KasynoPolska10.

Posted on

Range-Based EGARCH Option Pricing Models (REGARCH)

The research in this post and the related paper on Range Based EGARCH Option pricing Models is focused on the innovative range-based volatility models introduced in Alizadeh, Brandt, and Diebold (2002) (hereafter ABD).  We develop new option pricing models using multi-factor diffusion approximations couched within this theoretical framework and examine their properties in comparison with the traditional Black-Scholes model.

The two-factor version of the model, which I have applied successfully in various option arbitrage strategies, encapsulates the intuively appealing idea of a trending long term mean volatility process, around which oscillates a mean-reverting, transient volatility process.  The option pricing model also incorporates asymmetry/leverage effects and well as correlation effects between the asset return and volatility processes, which results in a volatility skew.

The core concept behind Range-Based Exponential GARCH model is Log-Range estimator discussed in an earlier post on volatility metrics, which contains a lengthy exposition of various volatility estimators and their properties. (Incidentally, for those of you who requested a copy of my paper on Estimating Historical Volatility, I have updated the post to include a link to the pdf).

SSALGOTRADING AD

We assume that the log stock price s follows a drift-less Brownian motion ds = sdW. The volatility of daily log returns, denoted h= s/sqrt(252), is assumed constant within each day, at ht from the beginning to the end of day t, but is allowed to change from one day to the next, from ht at the end of day t to ht+1 at the beginning of day t+1.  Under these assumptions, ABD show that the log range, defined as:

is to a very good approximation distributed as

where N[m; v] denotes a Gaussian distribution with mean m and variance v. The above equation demonstrates that the log range is a noisy linear proxy of log volatility ln ht.  By contrast, according to the results of Alizadeh, Brandt,and Diebold (2002), the log absolute return has a mean of 0.64 + ln ht and a variance of 1.11. However, the distribution of the log absolute return is far from Gaussian.  The fact that both the log range and the log absolute return are linear log volatility proxies (with the same loading of one), but that the standard deviation of the log range is about one-quarter of the standard deviation of the log absolute return, makes clear that the range is a much more informative volatility proxy. It also makes sense of the finding of Andersen and Bollerslev (1998) that the daily range has approximately the same informational content as sampling intra-daily returns every four hours.

Except for the model of Chou (2001), GARCH-type volatility models rely on squared or absolute returns (which have the same information content) to capture variation in the conditional volatility ht. Since the range is a more informative volatility proxy, it makes sense to consider range-based GARCH models, in which the range is used in place of squared or absolute returns to capture variation in the conditional volatility. This is particularly true for the EGARCH framework of Nelson (1990), which describes the dynamics of log volatility (of which the log range is a linear proxy).

ABD consider variants of the EGARCH framework introduced by Nelson (1990). In general, an EGARCH(1,1) model performs comparably to the GARCH(1,1) model of Bollerslev (1987).  However, for stock indices the in-sample evidence reported by Hentschel (1995) and the forecasting performance presented by Pagan and Schwert (1990) show a slight superiority of the EGARCH specification. One reason for this superiority is that EGARCH models can accommodate asymmetric volatility (often called the “leverage effect,” which refers to one of the explanations of asymmetric volatility), where increases in volatility are associated more often with large negative returns than with equally large positive returns.

The one-factor range-based model (REGARCH 1)  takes the form:

where the returns process Rt is conditionally Gaussian: Rt ~ N[0, ht2]

and the process innovation is defined as the standardized deviation of the log range from its expected value:

Following Engle and Lee (1999), ABD also consider multi-factor volatility models.  In particular, for a two-factor range-based EGARCH model (REGARCH2), the conditional volatility dynamics) are as follows:

and

where ln qt can be interpreted as a slowly-moving stochastic mean around which log volatility  ln ht makes large but transient deviations (with a process determined by the parameters kh, fh and dh).

The parameters q, kq, fq and dq determine the long-run mean, sensitivity of the long run mean to lagged absolute returns, and the asymmetry of absolute return sensitivity respectively.

The intuition is that when the lagged absolute return is large (small) relative to the lagged level of volatility, volatility is likely to have experienced a positive (negative) innovation. Unfortunately, as we explained above, the absolute return is a rather noisy proxy of volatility, suggesting that a substantial part of the volatility variation in GARCH-type models is driven by proxy noise as opposed to true information about volatility. In other words, the noise in the volatility proxy introduces noise in the implied volatility process. In a volatility forecasting context, this noise in the implied volatility process deteriorates the quality of the forecasts through less precise parameter estimates and, more importantly, through less precise estimates of the current level of volatility to which the forecasts are anchored.

read more…

2-Factor REGARCH Model for the S&P500 Index
Posted on

On Testing Direction Prediction Accuracy


As regards the question of forecasting accuracy discussed in the paper on Forecasting Volatility in the S&P 500 Index, there are two possible misunderstandings here that need to be cleared up.  These arise from remarks by one commentator  as follows:

“An above 50% vol direction forecast looks good,.. but “direction” is biased when working with highly skewed distributions!   ..so it would be nice if you could benchmark it against a simple naive predictors to get a feel for significance, -or- benchmark it with a trading strategy and see how the risk/return performs.”

(i) The first point is simple, but needs saying: the phrase “skewed distributions” in the context of volatility modeling could easily be misconstrued as referring to the volatility skew. This, of course, is used to describe to the higher implied vols seen in the Black-Scholes prices of OTM options. But in the Black-Scholes framework volatility is constant, not stochastic, and the “skew” referred to arises in the distribution of the asset return process, which has heavier tails than the Normal distribution (excess Kurtosis and/or skewness). I realize that this is probably not what the commentator meant, but nonetheless it’s worth heading that possible misunderstanding off at the pass, before we go on.

SSALGOTRADING AD

(ii) I assume that the commentator was referring to the skewness in the volatility process, which is characterized by the LogNormal distribution. But the forecasting tests referenced in the paper are tests of the ability of the model to predict the direction of volatility, i.e. the sign of the change in the level of volatility from the current period to the next period. Thus we are looking at, not a LogNormal distribution, but the difference in two LogNormal distributions with equal mean – and this, of course, has an expectation of zero. In other words, the expected level of volatility for the next period is the same as the current period and the expected change in the level of volatility is zero. You can test this very easily for yourself by generating a large number of observations from a LogNormal process, taking the difference and counting the number of positive and negative changes in the level of volatility from one period to the next. You will find, on average, half the time the change of direction is positive and half the time it is negative.

For instance, the following chart shows the distribution of the number of positive changes in the level of a LogNormally distributed random variable with mean and standard deviation of 0.5, for a sample of 1,000 simulations, each of 10,000 observations.  The sample mean (5,000.4) is very close to the expected value of 5,000.

Distribution Number of Positive Direction Changes

So, a naive predictor will forecast volatility to remain unchanged for the next period and by random chance approximately half the time volatility will turn out to be higher and half the time it will turn out to be lower than in the current period. Hence the default probability estimate for a positive change of direction is 50% and you would expect to be right approximately half of the time. In other words, the direction prediction accuracy of the naive predictor is 50%. This, then, is one of the key benchmarks you use to assess the ability of the model to predict market direction. That is what test statistics like Theil’s-U does – measures the performance relative to the naive predictor. The other benchmark we use is the change of direction predicted by the implied volatility of ATM options.
In this context, the model’s 61% or higher direction prediction accuracy is very significant (at the 4% level in fact) and this is reflected in the Theil’s-U statistic of 0.82 (lower is better). By contrast, Theil’s-U for the Implied Volatility forecast is 1.46, meaning that IV is a much worse predictor of 1-period-ahead changes in volatility than the naive predictor.

On its face, it is because of this exceptional direction prediction accuracy that a simple strategy is able to generate what appear to be abnormal returns using the change of direction forecasts generated by the model, as described in the paper. In fact, the situation is more complicated than that, once you introduce the concept of a market price of volatility risk.

 

Posted on

Long Memory and Regime Shifts in Asset Volatility

This post covers quite a wide range of concepts in volatility modeling relating to long memory and regime shifts and is based on an article that was published in Wilmott magazine and republished in The Best of Wilmott Vol 1 in 2005.  A copy of the article can be downloaded here.

One of the defining characteristics of volatility processes in general (not just financial assets) is the tendency for the serial autocorrelations to decline very slowly.  This effect is illustrated quite clearly in the chart below, which maps the autocorrelations in the volatility processes of several financial assets.

Thus we can say that events in the volatility process for IBM, for instance, continue to exert influence on the process almost two years later.

This feature in one that is typical of a black noise process – not some kind of rap music variant, but rather:

“a process with a 1/fβ spectrum, where β > 2 (Manfred Schroeder, “Fractals, chaos, power laws“). Used in modeling various environmental processes. Is said to be a characteristic of “natural and unnatural catastrophes like floods, droughts, bear markets, and various outrageous outages, such as those of electrical power.” Further, “because of their black spectra, such disasters often come in clusters.”” [Wikipedia].

Because of these autocorrelations, black noise processes tend to reinforce or trend, and hence (to some degree) may be forecastable.  This contrasts with a white noise process, such as an asset return process, which has a uniform power spectrum, insignificant serial autocorrelations and no discernable trending behavior:

White Noise Power Spectrum
White Noise Power Spectrum

An econometrician might describe this situation by saying that a  black noise process is fractionally integrated order d, where d = H/2, H being the Hurst Exponent.  A way to appreciate the difference in the behavior of a black noise process vs. a white process is by comparing two fractionally integrated random walks generated using the same set of quasi random numbers by Feder’s (1988) algorithm (see p 32 of the presentation on Modeling Asset Volatility).

Fractal Random Walk - White Noise
Fractal Random Walk – White Noise
Fractal Random Walk - Black Noise Process
Fractal Random Walk – Black Noise Process

As you can see. both random walks follow a similar pattern, but the black noise random walk is much smoother, and the downward trend is more clearly discernible.  You can play around with the Feder algorithm, which is coded in the accompanying Excel Workbook on Volatility and Nonlinear Dynamics .  Changing the Hurst Exponent parameter H in the worksheet will rerun the algorithm and illustrate a fractal random walk for a black noise (H > 0.5), white noise (H=0.5) and mean-reverting, pink noise (H<0.5) process.

One way of modeling the kind of behavior demonstrated by volatility process is by using long memory models such as ARFIMA and FIGARCH (see pp 47-62 of the Modeling Asset Volatility presentation for a discussion and comparison of various long memory models).  The article reviews research into long memory behavior and various techniques for estimating long memory models and the coefficient of fractional integration d for a process.

SSALGOTRADING AD

But long memory is not the only possible cause of long term serial correlation.  The same effect can result from structural breaks in the process, which can produce spurious autocorrelations.  The article goes on to review some of the statistical procedures that have been developed to detect regime shifts, due to Bai (1997), Bai and Perron (1998) and the Iterative Cumulative Sums of Squares methodology due to Aggarwal, Inclan and Leal (1999).  The article illustrates how the ICSS technique accurately identifies two changes of regimes in a synthetic GBM process.

In general, I have found the ICSS test to be a simple and highly informative means of gaining insight about a process representing an individual asset, or indeed an entire market.  For example, ICSS detects regime shifts in the process for IBM around 1984 (the time of the introduction of the IBM PC), the automotive industry in the early 1980’s (Chrysler bailout), the banking sector in the late 1980’s (Latin American debt crisis), Asian sector indices in Q3 1997, the S&P 500 index in April 2000 and just about every market imaginable during the 2008 credit crisis.  By splitting a series into pre- and post-regime shift sub-series and examining each segment for long memory effects, one can determine the cause of autocorrelations in the process.  In some cases, Asian equity indices being one example, long memory effects disappear from the series, indicating that spurious autocorrelations were induced by a major regime shift during the 1997 Asian crisis. In most cases, however, long memory effects persist.

Excel Workbook on Volatility and Nonlinear Dynamics 

There are several other topics from chaos theory and nonlinear dynamics covered in the workbook, including:

More on these issues in due course.

Posted on

Modeling Asset Volatility

I am planning a series of posts on the subject of asset volatility and option pricing and thought I would begin with a survey of some of the central ideas. The attached presentation on Modeling Asset Volatility sets out the foundation for a number of key concepts and the basis for the research to follow.

Perhaps the most important feature of volatility is that it is stochastic rather than constant, as envisioned in the Black Scholes framework.  The presentation addresses this issue by identifying some of the chief stylized facts about volatility processes and how they can be modelled.  Certain characteristics of volatility are well known to most analysts, such as, for instance, its tendency to “cluster” in periods of higher and lower volatility.  However, there are many other typical features that are less often rehearsed and these too are examined in the presentation.

Long Memory
For example, while it is true that GARCH models do a fine job of modeling the clustering effect  they typically fail to capture one of the most important features of volatility processes – long term serial autocorrelation.  In the typical GARCH model autocorrelations die away approximately exponentially, and historical events are seen to have little influence on the behaviour of the process very far into the future.  In volatility processes that is typically not the case, however:  autocorrelations die away very slowly and historical events may continue to affect the process many weeks, months or even years ahead.

Volatility Direction Prediction Accuracy
Volatility Direction Prediction Accuracy

There are two immediate and very important consequences of this feature.  The first is that volatility processes will tend to trend over long periods – a characteristic of Black Noise or Fractionally Integrated processes, compared to the White Noise behavior that typically characterizes asset return processes.  Secondly, and again in contrast with asset return processes, volatility processes are inherently predictable, being conditioned to a significant degree on past behavior.  The presentation considers the fractional integration frameworks as a basis for modeling and forecasting volatility.

Mean Reversion vs. Momentum
A puzzling feature of much of the literature on volatility is that it tends to stress the mean-reverting behavior of volatility processes.  This appears to contradict the finding that volatility behaves as a reinforcing process, whose long-term serial autocorrelations create a tendency to trend.  This leads to one of the most important findings about asset processes in general, and volatility process in particular: i.e. that the assets processes are simultaneously trending and mean-reverting.  One way to understand this is to think of volatility, not as a single process, but as the superposition of two processes:  a long term process in the mean, which tends to reinforce and trend, around which there operates a second, transient process that has a tendency to produce short term spikes in volatility that decay very quickly.  In other words, a transient, mean reverting processes inter-linked with a momentum process in the mean.  The presentation discusses two-factor modeling concepts along these lines, and about which I will have more to say later.

SSALGOTRADING AD

Cointegration
One of the most striking developments in econometrics over the last thirty years, cointegration is now a principal weapon of choice routinely used by quantitative analysts to address research issues ranging from statistical arbitrage to portfolio construction and asset allocation.  Back in the late 1990’s I and a handful of other researchers realized that volatility processes exhibited very powerful cointegration tendencies that could be harnessed to create long-short volatility strategies, mirroring the approach much beloved by equity hedge fund managers.  In fact, this modeling technique provided the basis for the Caissa Capital volatility fund, which I founded in 2002.  The presentation examines characteristics of multivariate volatility processes and some of the ideas that have been proposed to model them, such as FIGARCH (fractionally-integrated GARCH).

Dispersion Dynamics
Finally, one topic that is not considered in the presentation, but on which I have spent much research effort in recent years, is the behavior of cross-sectional volatility processes, which I like to term dispersion.  It turns out that, like its univariate cousin, dispersion displays certain characteristics that in principle make it highly forecastable.  Given an appropriate model of dispersion dynamics, the question then becomes how to monetize efficiently the insight that such a model offers.  Again, I will have much more to say on this subject, in future.

Posted on

A Meta-Strategy in S&P 500 E-Mini Futures

In earlier posts I have described the idea of a meta-strategy as a strategies that trades strategies.  It is an algorithm, or set of rules, that is used to decide when to trade an underlying strategy.  In some cases a meta-strategy may influence the size in which the underlying strategy is traded, or may even amend the base code.  In other word, a meta-strategy actively “trades” an underlying strategy, or group of strategies, much as in the same way a regular strategy may actively trade stocks, going long or short from time to time.  One distinction is that a meta-strategy will rarely, if ever, actually “short” an underlying strategy – at most it will simply turn the strategy off (reduce the position size to zero) for a period.

For a more detailed description, see this post:

Improving Trading System Performance Using a Meta-Strategy

In this post I look at a meta-strategy that developed for a client’s strategy in S&P E-Mini futures.  What is extraordinary is that the underlying strategy was so badly designed (not by me!) and performs so poorly that no rational systematic trader would likely give it  a second look –  instead he would toss it into the large heap of failed ideas that all quantitative researchers accumulate over the course of their careers.  So this is a textbook example that illustrates the power of meta-strategies to improve, or in this case transform, the performance of an underlying strategy.

1. The Strategy

The Target Trader Strategy (“TTS”) is a futures strategy applied to S&P 500 E-Mini futures that produces a very high win rate, but which occasionally experiences very large losses. The purpose of the analysis if to find methods that will:

1) Decrease the max loss / drawdown
2) Increase the win rate / profitability

For longs the standard setting is entry 40 ticks below the target, stop loss 1000 ticks below the target, and then 2 re-entries 100 ticks below entry 1 and 100 ticks below entry 2

For shorts the standard is entry 80 ticks above the target. stop loss 1000 ticks above the target, and then 2 re-entries 100 ticks above entry 1 and 100 ticks above entry 2

For both directions its 80 ticks above/below for entry 1, 1000 tick stop, and then 1 re entry 100 ticks above/below, and then re-entry 2 100 ticks above/below entry 2

 

2. Strategy Performance

2.1 Overall Performance

The overall performance of the strategy over the period from 2018 to 2020 is summarized in the chart of the strategy equity curve and table of performance statistics below.
These confirm that, while the win rate if very high (over 84%) there strategy experiences many significant drawdowns, including a drawdown of -$61,412.50 (-43.58%). The total return is of the order of 5% per year, the strategy profit factor is fractionally above 1 and the Sharpe Ratio is negligibly small. Many traders would consider the performance to be highly unattractive.

 

 

 

2.2 Long Trades

We break the strategy performance down into long and short trades, and consider them separately. On the long side, the strategy has been profitable, producing a gain of over 36% during the period 2018-2020. It also suffered catastrophic drawdown of over -$97,000 during that period:

 


 

 

2.3 Short Trades

On the short side, the story is even worse, producing an overall loss of nearly -$59,000:

 

 

 

3. Improving Strategy Performance with a Meta-Strategy

We considered two possible methods to improve strategy performance. The first method attempts to apply technical indicators and other data series to improve trading performance. Here we evaluated price series such as the VIX index and a wide selection of technical indicators, including RSI, ADX, Moving Averages, MACD, ATR and others. However, any improvement in strategy performance proved to be temporary in nature and highly variable, in many cases amplifying the problems with the strategy performance rather than improving them.

The second approach proved much more effective, however. In this method we create a meta-strategy which effectively “trades the strategy”, turning it on and off depending on its recent performance. The meta-strategy consists of a set of rules that determines whether or not to continue trading the strategy after a series of wins or losses. In some cases the meta-strategy may increase the trade size for a sequence of trades, at times when it considers the conditions for the underlying strategy to be favorable.

The result of applying the meta-strategy are described in the following sections.

3.1 Long & Short Strategies with Meta-Strategy Overlay

The performance of the long/short strategies combined with the meta-strategy overlay are set out in the chart and table below.
The overall improvements can be summarized as follows:

  • Net profit increases from $15,387 to $176,287
  • Account return rises from 15% to 176%
  • Percentage win rate rises from 84% to 95%
  • Profit factor increases from 1.0 to 6.7
  • Average trade rises from $51 to $2,631
  • Max $ Drawdown falls from -$61,412 to -$30,750
  • Return/Max Drawdown ratio rises from 0.35 to 5.85
  •  The modified Sharpe ratio increases from 0.07 to 0.5

Taken together, these are dramatic improvements to every important aspect of strategy performance.

There are two key rules in the meta-strategy, applicable to winning and losing trades:

Rule for winning trades:
After 3 wins in a row, skip the next trade.

Rule for losing trades:
After 3 losses in a row, add 1 contract until the first win. Subtract 1 contract after each win until the next loss, or back to 1 contract.

 

 

 

 

3.2 Long Trades with Meta-Strategy

The meta-strategy rules produce significant improvements in the performance of both the long and short components of the strategy. On the long side the percentage win rate is increased to 100% and the max % drawdown is reduced to 0%:

 

 

3.3 Short Trades with Meta-Strategy

Improvements to the strategy on the short side are even more significant, transforming a loss of -$59,000 into a profit of $91,600:

 

 

 

 

4. Conclusion

A meta-strategy is a simple, yet powerful technique that can transform the performance of an underlying strategy.  The rules are often simple, although they can be challenging to implement.  Meta strategies can be applied to almost any underlying strategy, whether in futures, equities, or forex. Worthwhile improvements in strategy performance are often achievable, although not often as spectacular as in this case.

If any reader is interested in designing a meta-strategy for their own use, please get in contact.

Posted on

Market Timing in the S&P 500 Index Using Volatility Forecasts

There has been a good deal of interest in the market timing ideas discussed in my earlier blog post Using Volatility to Predict Market Direction, which discusses the research of Diebold and Christoffersen into the sign predictability induced by volatility dynamics.  The ideas are thoroughly explored in a QuantNotes article from 2006, which you can download here.

There is a follow-up article from 2006 in which Christoffersen, Diebold, Mariano and Tay develop the ideas further to consider the impact of higher moments of the asset return distribution on sign predictability and the potential for market timing in international markets (download here).

Trading Strategy
To illustrate some of the possibilities of this approach, we constructed a simple market timing strategy in which a position was taken in the S&P 500 index or in 90-Day T-Bills, depending on an ex-ante forecast of positive returns from the logit regression model (and using an expanding window to estimate the drift coefficient).  We assume that the position is held for 30 days and rebalanced at the end of each period.  In this test we make no allowance for market impact, or transaction costs.

Results
Annual returns for the strategy and for the benchmark S&P 500 Index are shown in the figure below.  The strategy performs exceptionally well in 1987, 1989 and 1995, when the ratio between expected returns and volatility remains close to optimum levels and the direction of the S&P 500 Index is highly predictable,  Of equal interest is that the strategy largely avoids the market downturn of 2000-2002 altogether, a period in which sign probabilities were exceptionally low.

SSALGOTRADING AD

In terms of overall performance, the model enters the market in 113 out of a total of 241 months (47%) and is profitable in 78 of them (69%).  The average gain is 7.5% vs. an average loss of –4.11% (ratio 1.83).  The compound annual return is 22.63%, with an annual volatility of 17.68%, alpha of 14.9% and Sharpe ratio of 1.10.

The under-performance of the strategy in 2003 is explained by the fact that direction-of-change probabilities were rising from a very low base in Q4 2002 and do not reach trigger levels until the end of the year.  Even though the strategy out-performed the Index by a substantial margin of 6% , the performance in 2005 is of concern as market volatility was very low and probabilities overall were on a par with those seen in 1995.  Further tests are required to determine whether the failure of the strategy to produce an exceptional performance on par with 1995 was the result of normal statistical variation or due to changes in the underlying structure of the process requiring model recalibration.

Future Research & Development
The obvious next step is to develop the approach described above to formulate trading strategies based on sign forecasting in a universe of several assets, possibly trading binary options.  The approach also has potential for asset allocation, portfolio theory and risk management applications.

Market Timing in the S&amp;P500 Index
Market Timing in the S&P500 Index