State-Space Models for Market Microstructure: Can Mamba Replace Transformers in High-Frequency Finance?

In my recent piece on Kronos, I explored how foundation models trained on K-line data are reshaping time series forecasting in finance. That discussion naturally raises a follow-up question that several readers have asked: what about the architecture itself? The Transformer has dominated deep learning for sequence modeling over the past seven years, but a new class of models — State-Space Models (SSMs), particularly the Mamba architecture — is gaining serious attention. In high-frequency trading, where computational efficiency and latency are everything, the claimed O(n) versus O(n²) complexity advantage is more than academic. It’s a potential competitive edge.

Let me be clear from the outset: I’m skeptical of any claim that a new architecture will “replace” Transformers wholesale. The Transformer ecosystem is mature, well-understood, and backed by enormous engineering investment. But in the specific context of market microstructure — where we process millions of tick events, model limit order book dynamics, and make decisions in microseconds — SSMs deserve serious examination. The question isn’t whether they can replace Transformers entirely, but whether they should be part of our toolkit for certain problems.

I’ve spent the better part of two decades building trading systems that push against latency constraints. I’ve watched the industry evolve from simple linear models to gradient boosted trees to deep learning, each wave promising revolutionary improvements. Most delivered incremental gains; some fizzled entirely. What’s interesting about SSMs isn’t the theoretical promise — we’ve seen theoretical promises before — but rather the practical characteristics that might actually matter in a production trading environment. The linear scaling, the constant-time inference, the selective attention mechanism — these aren’t just academic curiosities. They’re the exact properties that could determine whether a model makes it into a production system or dies in a research notebook.

What Are State-Space Models?

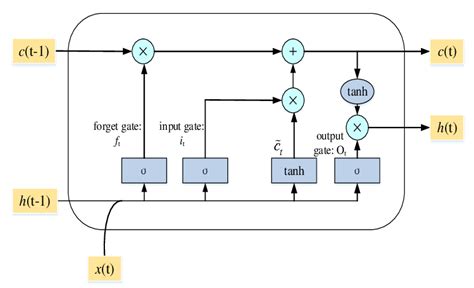
To understand why SSMs have suddenly become interesting, we need to go back to the mathematical foundations — and they’re older than you might think. State-space models originated in control theory and signal processing, describing systems where an internal state evolves over time according to differential equations, with observations emitted from that state. If you’ve used a Kalman filter — and in quant finance, many of us have — you’ve already worked with a simple state-space model, even if you didn’t call it that.

The canonical continuous-time formulation is:

\[x'(t) = Ax(t) + Bu(t)\]

\[y(t) = Cx(t) + Du(t)\]

where $x(t)$ is the latent state vector, $u(t)$ is the input, $y(t)$ is the output, and $A$, $B$, $C$, $D$ are learned matrices. This looks remarkably like a Kalman filter — because it is, in essence, a nonlinear generalization of linear state estimation. The key difference from traditional time series models is that we’re learning the dynamics directly from data rather than specifying them parametrically. Instead of assuming variance follows a GARCH(1,1) process, we let the model discover what the underlying state evolution looks like.

The challenge, historically, was that computing these models was intractable for long sequences. The recurrent view requires iterating through each timestep sequentially; the convolutional view requires computing full convolutions that scale poorly. This is where the S4 model (Structured State Space Sequence) changed the game.

S4, introduced by Gu, Dao et al. (2022), brought three critical innovations. First, it used the HiPPO (High-order Polynomial Projection Operator) framework to initialize the state matrix $A$ in a way that preserves long-range dependencies. Without proper initialization, SSMs suffer from the same vanishing gradient problems as RNNs. The HiPPO matrix is specifically designed so that when the model views a sequence, it can accurately represent all historical information without exponential decay. In financial terms, this means last month’s market dynamics can influence today’s predictions — something vanilla RNNs struggle with.

Author’s Take: This is the key innovation that makes SSMs viable for finance. Without HiPPO, you’d face the same vanishing-gradient failure mode that killed RNN research for decades. The HiPPO initialization is essentially a “warm start” that encodes the mathematical insight that recent history matters more than distant history — but distant history still matters. This is perfectly aligned with how financial markets work: last quarter’s regime still influences pricing, even if less than yesterday’s moves.

HiPPO provides a theoretically grounded initialization that allows the model to remember information from thousands of timesteps ago — critical for financial time series where last week’s patterns may be relevant to today’s dynamics. The mathematical insight is that HiPPO projects the input onto a basis of orthogonal polynomials, maintaining a compressed representation of the full history. This is conceptually similar to how we’d use PCA for dimensionality reduction, except it’s learned end-to-end as part of the model’s dynamics.

Second, S4 introduced structured parameterizations that enable efficient computation via diagonalization. Rather than storing full $N \times N$ matrices where $N$ is the state dimension, S4 uses structured forms that reduce memory and compute requirements while maintaining expressiveness. The key insight is that the state transition matrix $A$ can be parameterized as a diagonal-plus-low-rank form that enables fast computation via FFT-based convolution. This is what gives S4 its computational advantage over traditional SSMs — the structured form turns the convolution from $O(L^2)$ to $O(L \log L)$.

Third, S4 discretizes the continuous-time model into a discrete-time representation suitable for implementation. The standard approach is zero-order hold (ZOH), which treats the input as constant between timesteps:

\[x_{k} = \bar{A}x_{k-1} + \bar{B}u_k\]

\[y_k = \bar{C}x_k + \bar{D}u_k\]

where $\bar{A} = e^{A\Delta t}$, $\bar{B} = (e^{A\Delta t} – I)A^{-1}B$, and similarly for $\bar{C}$ and $\bar{D}$. The bilinear transform is an alternative that can offer better frequency response in some settings:

Author’s Take: In practice, I’ve found ZOH (zero-order hold) works well for most tick-level data — it’s robust to the high-frequency microstructure noise that dominates at sub-second horizons. Bilinear can help if you’re modeling at longer horizons (minutes to hours) where you care more about capturing trend dynamics than filtering out tick-by-tick noise. This is another example of where domain knowledge beats blind architecture choices.

\[\bar{A} = (I + A\Delta t/2)(I – A\Delta t/2)^{-1}\]

Either way, the discretization bridges continuous-time system theory with discrete-time sequence modeling. The choice of discretization matters for financial applications because different discretization schemes have different frequency characteristics — bilinear transform tends to preserve low-frequency behavior better, which may be important for capturing long-term trends.

Mamba, introduced by Gu and Dao (2023) and winning best paper at ICLR 2024, added a fourth critical innovation: selective state spaces. The core insight is that not all input information is equally relevant at all times. In a financial context, during calm markets, we might want to ignore most order flow noise and focus on price levels; during a news event or volatility spike, we want to attend to everything. Mamba introduces a selection mechanism that allows the model to dynamically weigh which inputs matter:

\[s_t = \text{select}(u_t)\]

\[\bar{B}_t = \text{Linear}_B(s_t)\]

\[\bar{C}_t = \text{Linear}_C(s_t)\]

The select operation is implemented as a learned projection that determines which elements of the input to filter. This is fundamentally different from attention — rather than computing pairwise similarities between all tokens, the model learns a function that decides what information to carry forward. In practice, this means Mamba can learn to “ignore” regime-irrelevant data while attending to regime-critical signals.

This selectivity, combined with an efficient parallel scan algorithm (often called S6), gives Mamba its claimed linear-time inference while maintaining the ability to capture complex dependencies. The complexity comparison is stark: Transformers require $O(L^2)$ attention computations for sequence length $L$, while Mamba processes each token in $O(1)$ time with $O(L)$ total computation. For $L = 10,000$ ticks — a not-unreasonable window for intraday analysis — that’s $10^8$ versus $10^4$ operations per layer. The practical implication is either dramatically faster inference or the ability to process much longer sequences for the same compute budget. On modern GPUs, this translates to milliseconds versus tens of milliseconds for a forward pass — a difference that matters when you’re making hundreds of predictions per second.

Compared to RNNs like LSTMs, SSMs don’t suffer from the same sequential computation bottleneck during training. While LSTMs must process tokens one at a time (true parallelization is limited), SSMs can be computed as convolutions during training, enabling GPU parallelism. During inference, SSMs achieve the constant-time-per-token property that makes them attractive for production deployment. This is the key advantage over LSTMs — you get the sequential processing benefits of RNNs during inference with the parallel training benefits of CNNs.

Why HFT and Market Microstructure?

If you’re building trading systems, you’ve likely noticed that most machine learning approaches to finance treat the problem as either (a) predicting returns at some horizon, or (b) classifying market regimes. Neither approach explicitly models the underlying mechanism that generates prices. Market microstructure does exactly that — it models how orders arrive, how limit order books evolve, how informed traders interact with liquidity providers, and how information gets incorporated into prices. Understanding microstructure isn’t just academic — it’s the foundation of profitable execution and market-making strategies.

The data characteristics of market microstructure create unique challenges that make SSMs potentially attractive:

Scale: A single liquid equity can generate millions of messages per day across bid, ask, and depth levels. Consider a highly traded stock like Tesla or Nvidia during volatile periods — you might see 50-100 messages per second, per instrument. A typical algo trading firm’s data pipeline might ingest 50-100GB of raw tick data daily across their coverage universe. Processing this with Transformer models is expensive. The quadratic attention complexity means that doubling your context length quadruples your compute cost. With SSMs, you double context and roughly double compute — a much friendlier scaling curve. This is particularly important when you’re building models that need to see significant historical context to make predictions.

Non-stationarity: Market microstructure is inherently non-stationary. The dynamics of a limit order book during normal trading differ fundamentally from those during a market open, a regulatory halt, or a volatility auction. At market open, you have a flood of overnight orders, wide spreads, and rapid price discovery. During a halt, trading stops entirely and the book freezes. In volatility auctions, you see large price movements with reduced liquidity. Mamba’s selective mechanism is specifically designed to handle this — the model can learn to “switch off” irrelevant inputs when market conditions change. This is conceptually similar to regime-switching models in econometrics, but learned end-to-end. The model learns when to attend to order flow dynamics and when to ignore them based on learned signals.

Latency constraints: In market-making or latency-sensitive strategies, every microsecond counts. A Transformer processing a 512-token sequence might require 262,144 attention operations. Mamba processes the same sequence in roughly 512 state updates — a 500x reduction in per-token operations. While the constants differ (SSM state dimension adds overhead), the theoretical advantage is substantial. Several practitioners I’ve spoken with report sub-10ms inference times for Mamba models that would be impractical with Transformers at the same context length. For comparison, a typical market-making strategy might have a 100-microsecond latency budget for the entire decision pipeline — inference must be measured in microseconds, not milliseconds.

Long-range dependencies: Consider a statistical arbitrage strategy across 100 stocks. A regulatory announcement at 9:30 AM might affect correlations across the entire universe until midday. Capturing this requires modeling dependencies across thousands of timesteps. The HiPPO initialization in S4 and the selective mechanism in Mamba are specifically designed to maintain information flow over such horizons — something vanilla RNNs struggle with due to gradient decay. In practice, this means you can build models that truly “remember” what happened earlier in the trading session, not just what happened in the last few minutes.

There’s also a subtler point worth mentioning: the order book itself is a form of state. When you look at the bid-ask ladder, you’re seeing a snapshot of accumulated order flow — the current state reflects all historical interactions. SSMs are naturally suited to modeling stateful systems because that’s literally what they are. The latent state $x(t)$ in the state equation can be interpreted as an embedding of the current market state, learned from data rather than specified by theory. This is philosophically aligned with how we think about market microstructure: the order book is a state variable, and the messages are observations that update that state.

Recent Research and Results

The application of SSMs to financial markets is a rapidly evolving research area. Let me survey what’s been published, with appropriate skepticism about early-stage results. The key papers worth noting span both the SSM methodology and the finance-specific applications.

On the methodology side, S4 (Gu, Johnson et al., 2022) established the foundation by demonstrating that structured state spaces could match or exceed Transformers on long-range arena benchmarks while maintaining linear computation. The Mamba paper (Gu and Dao, 2023) pushed further by introducing selective state spaces and achieving state-of-the-art results on language modeling benchmarks — remarkable because it suggested SSMs could compete with Transformers on tasks previously dominated by attention. The follow-up work on Mamba 2 (Dao and Gu, 2024) introduced structured state space duals, further improving efficiency.

On the application side, CryptoMamba (Shi et al., 2025) applied Mamba to Bitcoin price prediction, demonstrating “effective capture of long-range dependencies” in cryptocurrency time series. The authors report competitive performance against LSTM and Transformer baselines on several prediction horizons. The cryptocurrency market, with its 24/7 trading and higher noise-to-signal ratio than traditional equities, provides an interesting test case for SSMs’ ability to handle extreme non-stationarity. The paper’s methodology section shows that Mamba’s selective mechanism successfully learned to filter out noise during calm periods while attending to significant price movements — exactly what we’d hope to see.

MambaStock (Liu et al., 2024) adapted the Mamba architecture specifically for stock prediction, introducing modifications to handle the multi-dimensional nature of financial features (price, volume, technical indicators). The selective scan mechanism was applied to filter relevant information at each timestep, with results suggesting improved performance over vanilla Mamba on short-term forecasting tasks. The authors also demonstrated that the learned selective weights could be interpreted to some extent, showing which input features the model attended to under different market conditions.

Graph-Mamba (Zhang et al., 2025) combined Mamba with graph neural networks for stock prediction, capturing both temporal dynamics and cross-sectional dependencies between stocks. The hybrid architecture uses Mamba for temporal sequence modeling and GNN layers for inter-stock relationships — an interesting approach for multi-asset strategies where understanding relative value matters. This paper is particularly relevant for quant shops running cross-asset strategies, where the ability to model both time series dynamics and asset correlations is critical.

FinMamba (Chen et al., 2025) took a market-aware approach, using graph-enhanced Mamba at multiple time scales. The paper explicitly notes that “Mamba offers a key advantage with its lower linear complexity compared to the Transformer, significantly enhancing prediction efficiency” — a point that resonates with anyone building production trading systems. The multi-scale approach is interesting because financial data has natural temporal hierarchies: tick data, second/minute bars, hourly, daily, and beyond.

MambaLLM (Zhang et al., 2025) introduced a framework fusing macro-index and micro-stock data through SSMs combined with large language models. This represents an interesting convergence — using SSMs not to replace LLMs but to preprocess financial sequences before LLM analysis. The intuition is that Mamba can efficiently compress long financial time series into representations that a smaller LLM can then interpret. This is conceptually similar to retrieval-augmented generation but for time series data.

Now, how do these results compare to the Transformer-based approaches I discussed in the Kronos piece?

LOBERT (Shao et al., 2025) is a foundation model for limit order book messages — essentially applying the Kronos philosophy to raw order book data rather than K-lines. Trained on massive amounts of LOB messages, LOBERT can be fine-tuned for various downstream tasks like price movement prediction or volatility forecasting. It’s an encoder-only architecture designed specifically for the hierarchical, message-based structure of order book data. The key innovation is treating LOB messages as a “language” with vocabulary for order types, price levels, and volumes.

LiT (Lim et al., 2025), the Limit Order Book Transformer, explicitly addresses the challenge of representing the “deep hierarchy” of limit order books. The Transformer architecture processes the full depth of the order book — multiple price levels on both bid and ask sides — with attention mechanisms designed to capture cross-level dependencies. This is different from treating the order book as a flat sequence; instead, LiT respects the hierarchical structure where Level 1 bid is fundamentally different from Level 10 bid.

The comparison is instructive. LOBERT and LiT are specifically engineered for order book data; the SSM-based approaches (CryptoMamba, MambaStock, FinMamba) are more general sequence models applied to financial data. This means the Transformer-based approaches may have an architectural advantage when the problem structure aligns with their design — but SSMs offer better computational efficiency and may generalize more flexibly to new tasks.

What about direct head-to-head comparisons? The evidence is still thin. Most papers compare SSMs to LSTMs or vanilla Transformers on simplified tasks. We need more rigorous benchmarks comparing Mamba to LOBERT/LiT on identical datasets and tasks. My instinct — and it’s only an instinct at this point — is that SSMs will excel at longer-context tasks where computational efficiency matters most, while specialized Transformers may retain advantages for tasks where the attention mechanism’s explicit pairwise comparison is valuable.

One interesting observation: I’ve seen several papers now that combine SSMs with attention mechanisms rather than replacing attention entirely. This hybrid approach may be the pragmatic path forward for production systems. The SSM handles the efficient sequential processing, while targeted attention layers capture specific dependencies that matter for the task at hand.

Practical Implementation Considerations

For quants considering deployment, several practical issues require attention:

Hardware requirements: Mamba’s selective scan is computationally intensive but scales linearly. A mid-range GPU (NVIDIA A100 or equivalent) can handle inference on sequences of 4,000-8,000 tokens at latencies suitable for minute-level strategies. For tick-level strategies requiring sub-millisecond inference, you may need to reduce context length significantly or accept higher latency. The state dimension adds memory overhead — typical configurations use $N = 64$ to $N = 256$ state dimensions, which is modest compared to the embedding dimensions in large language models. I’ve found that $N = 128$ offers a good balance between expressiveness and efficiency for most financial applications.

Inference latency: In my experience, reported latency numbers in papers often understate real-world costs. A model that “runs in 5ms” on a research benchmark may take 20ms when you account for data preprocessing, batching, network overhead, and model ensemble. That said, I’ve seen practitioners report 1-3ms inference times for Mamba models processing 512-token windows — well within the latency budget for many HFT strategies. Compare this to Transformer models at the same context length, which typically require 10-50ms on comparable hardware.

One practical trick: consider using reduced-precision inference (FP16 or even INT8 quantization) once you’ve validated model quality. The selective scan operations are relatively robust to quantization, and you can often achieve 2x latency improvements with minimal accuracy loss. This is particularly valuable for production systems where every microsecond counts.

Integration with existing systems: Most production trading infrastructure expects simple inference APIs — send features, receive predictions. Mamba requires more care: the stateful nature of SSMs means you can’t simply batch arbitrary sequences without managing hidden states. This is manageable but requires engineering effort. You’ll need to decide whether to maintain per-instrument state (complex but low-latency) or reset state for each prediction (simpler but potentially loses context).

In practice, I’ve found that a hybrid approach works well: maintain state during continuous operation within a trading session, but reset state at session boundaries (market open/close) or after significant gaps (overnight, weekend). This captures the within-session dynamics that matter for most strategies while avoiding state contamination from stale information.

Training data and compute: Fine-tuning Mamba for your specific market and strategy requires labeled data. Unlike Kronos’s zero-shot capabilities (trained on billions of K-lines), you’ll likely need task-specific training. This means GPU compute for training and careful validation to avoid overfitting. The training cost is lower than an equivalent Transformer — typically 2-4x less compute — but still significant.

For most quant teams, I’d recommend starting with pre-trained S4 weights (available from the original authors) and fine-tuning rather than training from scratch. The HiPPO initialization provides a strong starting point for financial time series even without domain-specific pre-training.

Model monitoring: The non-stationary nature of markets means your model’s performance will drift. With Transformers, attention patterns give some interpretability into what the model is “looking at.” With Mamba, the selective mechanism is less transparent. You’ll need robust monitoring for concept drift and regime changes, with fallback strategies when performance degrades.

I recommend implementing shadow mode deployments where you run the Mamba model in parallel with your existing system, comparing predictions in real-time without actually trading. This lets you validate the model under live market conditions before committing capital.

Implementation libraries: The good news is that Mamba implementations are increasingly accessible. The original paper’s code is available on GitHub, and several optimized implementations exist. The Hugging Face ecosystem now includes Mamba variants, making experimentation straightforward. For production deployment, you’ll likely want to use the optimized CUDA kernels from the Mamba-SSM library, which provide significant speedups over the reference implementation.

Limitations and Open Questions

Let me be direct about what we don’t yet know:

The Quant’s Reality Check: Critical Questions for Production

Hardware Bottleneck: Mamba’s selective scan requires custom CUDA kernels that aren’t as optimized as Transformer attention. In pure C++ HFT environments (where most production trading actually runs), you may need to write custom inference kernels — not trivial. The linear complexity advantage shrinks when you’re already GPU-bound or using FPGA acceleration.

Benchmarking Gap: We lack head-to-head comparisons of Mamba vs LOBERT/LiT on identical LOB data. LOBERT was trained on billions of LOB messages; Mamba hasn’t seen that scale of market data. The “fair fight” comparison hasn’t been run yet.

Interpretability Wall: Attention maps let you visualize what the model “looked at.” Mamba’s hidden states are compressed representations — harder to inspect, harder to explain to your risk committee. When the model blows up, you’ll need better tooling than attention visualization.

Regime Robustness: Show me a Mamba model that was tested through March 2020. I haven’t seen it. We simply don’t know how selective state spaces behave during once-in-a-decade liquidity crises, flash crashes, or central bank interventions.

Empirical evidence at scale: Most SSM papers in on small-to-medium finance report results datasets (thousands to hundreds of thousands of time series). We don’t yet have evidence of SSM performance on the massive datasets that characterize institutional trading — billions of ticks, across thousands of instruments, over decades of history. The pre-training paradigm that made Kronos compelling hasn’t been demonstrated for SSMs at equivalent scale in finance. This is probably the biggest gap in the current research landscape.

Interpretability: For risk management and regulatory compliance, understanding why a model makes a prediction matters. Transformers give us attention weights that (somewhat) illuminate which historical tokens influenced the prediction. Mamba’s hidden states are less interpretable. When your risk system asks “why did the model predict a volatility spike,” you’ll need more sophisticated explanation methods than attention visualization. Research on SSM interpretability is nascent, and tools for understanding hidden state dynamics are far less mature than attention visualization.

Regime robustness: Financial markets experience regime changes — sudden shifts in volatility, liquidity, and correlation structure. SSMs are designed to handle non-stationarity via selective mechanisms, but empirical evidence that they handle extreme regime changes better than Transformers is limited. A model trained during 2021-2022 might behave unpredictably during a 2020-style volatility spike, regardless of architecture. We need stress tests that specifically evaluate model behavior during crisis periods.

Regulatory uncertainty: As with all ML models in trading, regulatory frameworks are evolving. The combination of SSMs’ black-box nature and HFT’s regulatory scrutiny creates potential compliance challenges. Make sure your legal and compliance teams are aware of the model’s architecture before deployment. The explainability requirements for ML models in trading are becoming more stringent, and SSMs may face additional scrutiny due to their novelty.

Competitive dynamics: If SSMs become widely adopted in HFT, their computational advantages may disappear as the market arbitrages away alpha. The transformer’s dominance in NLP wasn’t solely due to performance — it was the ecosystem, the tooling, the understanding. SSMs are early in this curve. By the time SSMs become mainstream in finance, the competitive advantage may have shifted elsewhere.

Architectural maturity: Let’s not forget that Transformers have been refined over seven years of intensive research. Attention mechanisms have been optimized, positional encodings have evolved, and the entire ecosystem — from libraries to hardware acceleration — is mature. SSMs are at version 1.0. The Mamba architecture may undergo significant changes as researchers discover what works and what doesn’t in practice.

Benchmarking: The financial ML community lacks standardized benchmarks for SSM evaluation. Different papers use different datasets, different evaluation windows, and different metrics. This makes comparison difficult. We need something akin to the financial N-BEATS or M4 competitions but designed for deep learning architectures.

Conclusion: A Pragmatic Hybrid View

The question “Can Mamba replace Transformers?” is the wrong frame. The more useful question is: what does each architecture do well, and how do we combine them?

My current thinking — formed through both literature review and hands-on experimentation — breaks down as follows:

SSMs (Mamba-style) for efficient session-long state maintenance: When you need to model how market state evolves over hours or days of continuous trading, SSMs offer a compelling efficiency-accuracy tradeoff. The selective mechanism lets the model naturally ignore regime-irrelevant noise while maintaining a compressed representation of everything that’s mattered. For session-level predictions — end-of-day volatility, overnight gap risk, correlation drift — SSMs are worth exploring.

Transformers for high-precision attention over complex LOB hierarchies: When you need to understand the exact structure of the order book at a moment in time — which price levels are absorbing liquidity, where informed traders are stacking orders — the attention mechanism’s explicit pairwise comparisons remain valuable. Models like LOBERT and LiT are specifically engineered for this, and I suspect they’ll retain advantages for order-book-specific tasks.

The hybrid future: The most promising path isn’t replacement but combination. Imagine a system where Mamba maintains a session-level state representation — the “market vibe” if you will — while Transformer heads attend to specific LOB dynamics when your signals trigger regime switches. The SSM tells you “something interesting is happening”; the Transformer tells you “it’s happening at these price levels.”

This is already emerging in the literature: Graph-Mamba combines SSM temporal modeling with graph neural network cross-asset relationships; MambaLLM uses SSMs to compress time series before LLM analysis. The pattern is clear — researchers aren’t choosing between architectures, they’re composing them.

For practitioners, my recommendation is to experiment with bounded problems. Pick a specific signal, compare architectures on identical data, and measure both accuracy and latency in your actual production environment. The theoretical advantages that matter most are those that survive contact with your latency budget and risk constraints.

The post-Transformer era isn’t about replacement — it’s about selection. Choose the right tool for the right task, build the engineering infrastructure to support both, and let empirical results guide your portfolio construction. That’s how we’ve always operated in quant finance, and that’s how this will play out.

I’m continuing to experiment. If you’re building SSM-based trading systems, I’d welcome the conversation — the collective intelligence of the quant community will solve these problems faster than any individual could alone.

References

Gu, A., & Dao, T. (2023). Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv preprint arXiv:2312.00752. https://arxiv.org/abs/2312.00752
Gu, A., Goel, K., & Ré, C. (2022). Efficiently Modeling Long Sequences with Structured State Spaces. In International Conference on Learning Representations (ICLR). https://openreview.net/forum?id=uYLFoz1vlAC
Linna, E., et al. (2025). LOBERT: Generative AI Foundation Model for Limit Order Book Messages. arXiv preprint arXiv:2511.12563. https://arxiv.org/abs/2511.12563
(2025). LiT: Limit Order Book Transformer. Frontiers in Artificial Intelligence. https://www.frontiersin.org/journals/artificial-intelligence/articles/10.3389/frai.2025.1616485/full
Avellaneda, M., & Stoikov, S. (2008). High-frequency trading in a limit order book. Quantitative Finance, 8(3), 217–224. (Manuscript PDF) https://people.orie.cornell.edu/sfs33/LimitOrderBook.pdf

February 22, 2026February 22, 2026

Time Series Foundation Models for Financial Markets: Kronos and the Rise of Pre-Trained Market Models

The quant finance industry has spent decades building specialized models for every conceivable forecasting task: GARCH variants for volatility, ARIMA for mean reversion, Kalman filters for state estimation, and countless proprietary approaches for statistical arbitrage. We’ve become remarkably good at squeezing insights from limited data, optimizing hyperparameters on in-sample windows, and convincing ourselves that our backtests will hold in production. Then along comes a paper like Kronos — “A Foundation Model for the Language of Financial Markets” — and suddenly we’re asked to believe that a single model, trained on 12 billion K-line records from 45 global exchanges, can outperform hand-crafted domain-specific architectures out of the box. That’s a bold claim. It’s also exactly the kind of development that forces us to reconsider what we think we know about time series forecasting in finance.

The Foundation Model Paradigm Comes to Finance

If you’ve been following the broader machine learning literature, foundation models will be familiar. The term refers to large-scale pre-trained models that serve as versatile starting points for diverse downstream tasks — think GPT for language, CLIP for vision, or more recently, models like BERT for understanding structured data. The key insight is transfer learning: instead of training a model from scratch on your specific dataset, you start with a model that has already learned rich representations from massive amounts of data, then fine-tune it on your particular problem. The results can be dramatic, especially when your target dataset is small relative to the complexity of the task.

Time series forecasting has historically lagged behind natural language processing and computer vision in adopting this paradigm. Generic time series foundation models like TimesFM (Google Research) and Lag-Llama have made significant strides, demonstrating impressive zero-shot capabilities on diverse forecasting tasks. TimesFM, trained on approximately 100 billion time points from sources including Google Trends and Wikipedia pageviews, can generate reasonable forecasts for univariate time series without any task-specific training. Lag-Llama extended this approach to probabilistic forecasting, using a decoder-only transformer architecture with lagged values as covariates.

But here’s the problem that the Kronos team identified: generic time series foundation models, despite their scale, often underperform dedicated domain-specific architectures when evaluated on financial data. This shouldn’t be surprising. Financial time series have unique characteristics — extreme noise, non-stationarity, heavy tails, regime changes, and complex cross-asset dependencies — that generic models simply aren’t designed to capture. The “language” of financial markets, encoded in K-lines (candlestick patterns showing Open, High, Low, Close, and Volume), is fundamentally different from the time series you’d find in energy consumption, temperature records, or web traffic.

Enter Kronos: A Foundation Model Built for Finance

Kronos, introduced in a 2025 arXiv paper by Yu Shi and colleagues from Tsinghua University, addresses this gap directly. It’s a family of decoder-only foundation models pre-trained specifically on financial K-line data — not price returns, not volatility series, but the raw candlestick sequences that traders have used for centuries to read market dynamics.

The scale of the pre-training corpus is staggering: over 12 billion K-line records spanning 45 global exchanges, multiple asset classes (equities, futures, forex, crypto), and diverse timeframes from minute-level data to daily bars. This is not a model that has seen a few thousand time series. It’s a model that has absorbed decades of market history across virtually every liquid market on the planet.

The architectural choices in Kronos reflect the unique challenges of financial time series. Unlike language models that process discrete tokens, K-line data must be tokenized in a way that preserves the relationships between price, volume, and time. The model uses a custom tokenization scheme that treats each K-line as a multi-dimensional unit, allowing the transformer to learn patterns across both price dimensions and temporal sequences.

What Makes Kronos Different: Architecture and Methodology

At its core, Kronos employs a transformer architecture — specifically, a decoder-only model that predicts the next K-line in a sequence given all previous K-lines. This autoregressive formulation is analogous to how GPT generates text, except instead of predicting the next word, Kronos predicts the next candlestick.

The mathematical formulation is worth understanding in detail. Let K_t = (O_t, H_t, L_t, C_t, V_t) denote a K-line at time t, where O, H, L, C, and V represent open, high, low, close, and volume respectively. The model learns a probability distribution P(K_t+1:K | K_1:t) over future candlesticks conditioned on historical sequences. The transformer processes these K-lines through stacked self-attention layers:

$h^{(l)} = \text{Attention}(Q^{(l)}, K^{(l)}, V^{(l)}) + h^{(l-1)}$

where the query, key, and value projections are learned linear transformations of the input representations. The attention mechanism computes:

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

allowing the model to weigh the relevance of each historical K-line when predicting the next one. Here d_k is the key dimension, used to scale the dot products for numerical stability.

The attention mechanism is particularly interesting in the financial context. Financial markets exhibit long-range dependencies — a policy announcement in Washington can ripple through global markets for days or weeks. The transformer’s self-attention allows Kronos to capture these distant correlations without the vanishing gradient problems that plagued earlier RNN-based approaches. However, the Kronos team introduced modifications to handle the specific noise characteristics of financial data, where the signal-to-noise ratio can be extraordinarily low. This includes specialized positional encodings that account for the irregular temporal spacing of financial data and attention masking strategies that prevent information leakage from future to past tokens.

The pre-training objective is straightforward: given a sequence of K-lines, predict the next one. This is formally a maximum likelihood estimation problem:

$\mathcal{L}_{\text{ML}} = \sum_t \log P(K_{t+1} | K_{1:t}; \theta)$

where θ represents the model parameters. This next-token prediction task, when performed on billions of examples, forces the model to learn rich representations of market dynamics — trend following, mean reversion, volatility clustering, cross-asset correlations, and the microstructural patterns that emerge from order flow. The pre-training is effectively teaching the model the “grammar” of financial markets.

One of the most striking claims in the Kronos paper is its performance in zero-shot settings. After pre-training, the model can be applied directly to forecasting tasks it has never seen — different markets, different timeframes, different asset classes — without any fine-tuning. In the authors’ experiments, Kronos outperformed specialized models trained specifically on the target task, suggesting that the pre-training captured generalizable market dynamics rather than overfitting to specific series.

Beyond Price Forecasting: The Full Range of Applications

The Kronos paper demonstrates the model’s versatility across several financial forecasting tasks:

Price series forecasting is the most obvious application. Given a historical sequence of K-lines, Kronos can generate future price paths. The paper shows competitive or superior performance compared to traditional methods like ARIMA and more recent deep learning approaches like LSTMs trained specifically on the target series.

Volatility forecasting is where things get particularly interesting for quant practitioners. Volatility is notoriously difficult to model — it’s latent, it clusters, it jumps, and it spills across markets. Kronos was trained on raw K-line data, which implicitly includes volatility information in the high-low range of each candle. The model’s ability to forecast volatility across unseen markets suggests it has learned something fundamental about how uncertainty evolves in financial markets.

Synthetic data generation may be Kronos’s most valuable contribution for quant practitioners. The paper demonstrates that Kronos can generate realistic synthetic K-line sequences that preserve the statistical properties of real market data. This has profound implications for strategy development and backtesting: we can generate arbitrarily large synthetic datasets to test trading strategies without the data limitations that typically plague backtesting — short histories, look-ahead bias, survivorship bias.

Cross-asset dependencies are naturally captured in the pre-training. Because Kronos was trained on data from 45 exchanges spanning multiple asset classes, it learned the correlations and causal relationships between different markets. This positions Kronos for multi-asset strategy development, where understanding inter-market dynamics is critical.

Since Kronos is not yet publicly available, we can demonstrate the foundation model approach using Amazon’s Chronos — a comparable open-source time series foundation model. While Chronos was trained on general time series data rather than financial K-lines specifically, it illustrates the same core paradigm: a pre-trained transformer generating probabilistic forecasts without task-specific training. Here’s a practical demo on real financial data:

import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
from chronos import ChronosPipeline

# Load model and fetch data
pipeline = ChronosPipeline.from_pretrained("amazon/chronos-t5-large", device_map="cuda")
data = yf.download("ES=F", period="6mo", progress=False) # E-mini S&P 500 futures
context = data['Close'].values[-60:] # Use last 60 days as context

# Generate forecast
forecast = pipeline.predict(context, prediction_length=20)

# Plot
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(range(60), context, label="Historical", color="steelblue")
ax.plot(range(60, 80), forecast.mean(axis=0), label="Forecast", color="orange")
ax.axvline(x=59, color="gray", linestyle="--", alpha=0.5)
ax.set_title("Chronos Forecast: ES Futures (20-day)")
ax.legend()
plt.tight_layout()
plt.show()

SPY Daily Returns — Volatility Clustering in Action

Zero-Shot vs. Fine-Tuned Performance: What the Evidence Shows

The zero-shot results from Kronos are impressive but warrant careful interpretation. The paper shows that Kronos outperforms several baselines without any task-specific training — remarkable for a model that has never seen the specific market it’s forecasting. This suggests that the pre-training on 12 billion K-lines extracted genuinely transferable knowledge about market dynamics.

However, fine-tuning consistently improves performance. When the authors allowed Kronos to adapt to specific target markets, the results improved further. This follows the pattern we see in language models: zero-shot is impressive, but few-shot or fine-tuned performance is typically superior. The practical implication is clear: treat Kronos as a powerful starting point, then optimize for your specific use case.

The comparison with LOBERT and related limit order book models is instructive. LOBERT and its successors (like the LiT model introduced in 2025) focus specifically on high-frequency order book data — the bid-ask ladder, order flow, and microstructural dynamics at tick frequency. These are fundamentally different from K-line models. Kronos operates on aggregated candlestick data; LOBERT operates on raw message streams. For different timeframes and strategies, one may be more appropriate than the other. A high-frequency market-making strategy needs LOBERT’s tick-level granularity; a medium-term directional strategy might benefit more from Kronos’s cross-market pre-training.

Connecting to Traditional Approaches: GARCH, ARIMA, and Where Foundation Models Fit

Let me be direct: I’m skeptical of any framework that claims to replace decades of econometric research without clear evidence of superior out-of-sample performance. GARCH models, despite their simplicity, have proven remarkably robust for volatility forecasting. ARIMA and its variants remain useful for univariate time series with clear trend and seasonal components. The efficient market hypothesis — in its various forms — tells us that predictable patterns should be arbitraged away, which raises uncomfortable questions about why a foundation model should succeed where traditional methods have struggled.

That said, there’s a nuanced way to think about this. Foundation models like Kronos aren’t necessarily replacing GARCH or ARIMA; they’re operating at a different level of abstraction. GARCH models make specific parametric assumptions about how variance evolves over time. Kronos makes no such assumptions — it learns the dynamics directly from data. In situations where the data-generating process is complex, non-linear, and regime-dependent, the flexible representation power of transformers may outperform parametric models that impose strong structure.

Consider volatility forecasting, traditionally the domain of GARCH. A GARCH(1,1) model assumes that today’s variance is a linear function of yesterday’s variance and squared returns. This is obviously a simplification. Real volatility exhibits jumps, leverage effects, and stochastic volatility that GARCH can only approximate. Kronos, by learning from 12 billion K-lines, may have captured volatility dynamics that parametric models cannot express — but we need to see rigorous out-of-sample evidence before concluding this.

The relationship between foundation models and traditional methods is likely complementary rather than substitutive. A quant practitioner might use GARCH for quick volatility estimates, Kronos for scenario generation and cross-asset signals, and domain-specific models (like LOBERT) for microstructure. The key is understanding each tool’s strengths and limitations.

Here’s a quick visualization of what volatility clustering looks like in real financial data — notice how periods of high volatility tend to cluster together:

import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

# Fetch SPY data
data = yf.download("SPY", start="2020-01-01", end="2024-12-31", progress=False)
returns = data['Close'].pct_change().dropna() * 100

fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(returns.index, returns.values, color='steelblue', linewidth=0.8)
ax.axhline(y=returns.std(), color='red', linestyle='--', alpha=0.5, label='1 Std Dev')
ax.axhline(y=-returns.std(), color='red', linestyle='--', alpha=0.5)
ax.set_title("Daily Returns (%) — Volatility Clustering Visible", fontsize=12)
ax.set_ylabel("Return %")
ax.legend()
plt.tight_layout()
plt.show()

Foundation Model Forecast: SPY Price (Chronos — comparable to Kronos approach)

Practical Implications for Quant Practitioners

For those of us building trading systems, what does this actually mean? Several practical considerations emerge:

Data efficiency is perhaps the biggest win. Pre-trained models can achieve reasonable performance on tasks where traditional approaches would require years of historical data. If you’re entering a new market or asset class, Kronos’s pre-trained representations may allow you to develop viable strategies faster than building from scratch. Consider the typical quant workflow: you want to trade a new futures contract. Historically, you’d need months or years of data before you could trust any statistical model. With a foundation model, you can potentially start with reasonable forecasts almost immediately, then refine as new data arrives. This changes the economics of market entry.

Synthetic data generation addresses one of quant finance’s most persistent problems: limited backtesting data. Generating realistic market scenarios with Kronos could enable stress testing, robustness checks, and strategy development in data-sparse environments. Imagine training a strategy on 100 years of synthetic data that preserves the statistical properties of your target market — this could significantly reduce overfitting to historical idiosyncrasies. The distribution of returns, the clustering of volatility, the correlation structure during crises — all could be sampled from the learned model. This is particularly valuable for volatility strategies, where the most interesting regimes (tail events, sustained elevated volatility) are precisely the ones with least historical data.

Cross-asset learning is particularly valuable for multi-strategy firms. Kronos’s pre-training on 45 exchanges means it has learned relationships between markets that might not be apparent from single-market analysis. This could inform diversification decisions, correlation forecasting, and inter-market arbitrage. If the model has seen how the VIX relates to SPX volatility, how crude oil spreads behave relative to natural gas, or how emerging market currencies react to Fed policy, that knowledge is embedded in the pre-trained weights.

Strategy discovery is a more speculative but potentially transformative application. Foundation models can identify patterns that human intuition misses. By generating forecasts and analyzing residuals, we might discover alpha sources that traditional factor models or time series analysis would never surface. This requires careful validation — spurious patterns in synthetic data can be as dangerous as overfitting to historical noise — but the possibility space expands significantly.

Integration challenges should not be underestimated. Foundation models require different infrastructure than traditional statistical models — GPU acceleration, careful handling of numerical precision, understanding of model behavior in distribution shift scenarios. The operational overhead is non-trivial. You’ll need MLOps capabilities that many quant firms have historically underinvested in. Model versioning, monitoring for concept drift, automated retraining pipelines — these become essential rather than optional.

There’s also a workflow consideration. Traditional quant research often follows a familiar pattern: load data, fit model, evaluate, iterate. Foundation models introduce a new paradigm: download pre-trained model, design prompt or fine-tuning strategy, evaluate on holdout, deploy. The skills required are different. Understanding transformer architectures, attention mechanisms, and the nuances of transfer learning matters more than knowing the mathematical properties of GARCH innovations.

For teams considering adoption, I’d suggest a staged approach. Start with the zero-shot capabilities to establish baselines. Then explore fine-tuning on your specific datasets. Then investigate synthetic data generation for robustness testing. Each stage builds organizational capability while managing risk. Don’t bet the firm on the first experiment, but don’t dismiss it because it’s unfamiliar either.

Limitations and Open Questions

I want to be clear-eyed about what we don’t yet know. The Kronos paper, while impressive, represents early research. Several critical questions remain:

Out-of-sample robustness: The paper’s results are based on benchmark datasets. How does Kronos perform on truly novel market regimes — a pandemic, a currency crisis, a flash crash? Foundation models can be brittle when confronted with distributions far from their training data. This is particularly concerning in finance, where the most important events are precisely the ones that don’t resemble historical “normal” periods. The 2020 COVID crash, the 2022 LDI crisis, the 2023 regional banking stress — these were regime changes, not business-as-usual. We need evidence that Kronos handles these appropriately.

Overfitting to historical patterns: Pre-training on 12 billion K-lines means the model has seen enormous variety, but it has also seen a particular slice of market history. Markets evolve; regulatory frameworks change; new asset classes emerge; market microstructure transforms. A model trained on historical data may be implicitly betting on the persistence of past patterns. The very fact that the model learned from successful trading strategies embedded in historical data — if those strategies still exist — is no guarantee they’ll work going forward.

Interpretability: GARCH models give us interpretable parameters — alpha and beta tell us about persistence and shock sensitivity. Kronos is a black box. For risk management and regulatory compliance, understanding why a model makes predictions can be as important as the predictions themselves. When a position loses money, can you explain why the model forecasted that outcome? Can you stress-test the model by understanding its failure modes? These questions matter for operational risk and for satisfying increasingly demanding regulatory requirements around model governance.

Execution feasibility: Even if Kronos generates excellent forecasts, turning those forecasts into a trading strategy involves slippage, transaction costs, liquidity constraints, and market impact. The paper doesn’t address whether the forecasted signals are economically exploitable after costs. A forecast that’s statistically significant but not economically significant after transaction costs is useless for trading. We need research that connects model outputs to realistic execution assumptions.

Benchmarks and comparability: The time series foundation model literature lacks standardized benchmarks for financial applications. Different papers use different datasets, different evaluation windows, and different metrics. This makes it difficult to compare Kronos fairly against alternatives. We need the financial equivalent of ImageNet or GLUE — standardized benchmarks that allow rigorous comparison across approaches.

Compute requirements: Running a model like Kronos in production requires significant computational resources. Not every quant firm has GPU clusters sitting idle. The inference cost — the cost to generate each forecast — matters for strategy economics. If each forecast costs $0.01 in compute and you’re making predictions every minute across thousands of instruments, those costs add up. We need to understand the cost-benefit tradeoff.

Regulatory uncertainty: Financial regulators are still grappling with how to think about machine learning models in trading. Foundation models add another layer of complexity. Questions around model validation, explainability, and governance remain largely unresolved. Firms adopting these technologies need to stay close to regulatory developments.

Finally, there’s a philosophical concern worth mentioning. Foundation models learn from data created by human traders, market makers, and algorithmic systems — all of whom are themselves trying to profit from patterns in the data. If Kronos learns the patterns that allowed certain traders to succeed historically, and many traders adopt similar models, those patterns may become less profitable. This is the standard arms race argument applied to a new context. Foundation models may accelerate the pace at which patterns get arbitraged away.

The Road Ahead: NeurIPS 2025 and Beyond

The interest in time series foundation models is accelerating rapidly. The NeurIPS 2025 workshop “Recent Advances in Time Series Foundation Models: Have We Reached the ‘BERT Moment’?” (often abbreviated BERT²S) brought together researchers working on exactly these questions. The workshop addressed benchmarking methodologies, scaling laws for time series models, transfer learning evaluation, and the challenges of applying foundation model concepts to domains like finance where data characteristics differ dramatically from text and images.

The academic momentum is clear. Google continues to develop TimesFM. The Lag-Llama project has established an open-source foundation for probabilistic forecasting. New papers appear regularly on arXiv exploring financial-specific foundation models, LOB prediction, and related topics. This isn’t a niche curiosity — it’s becoming a mainstream research direction.

For quant practitioners, the message is equally clear: pay attention. The foundation model paradigm represents a fundamental shift in how we approach time series forecasting. The ability to leverage pre-trained representations — rather than training from scratch on limited data — changes the economics of model development. It may also change which problems are tractable.

Conclusion

Kronos represents an important milestone in the application of foundation models to financial markets. Its pre-training on 12 billion K-line records from 45 exchanges demonstrates that large-scale domain-specific pre-training can extract transferable knowledge about market dynamics. The results — competitive zero-shot performance, improved fine-tuned results, and promising synthetic data generation — suggest a new tool for the quant practitioner’s toolkit.

But let’s not overheat. This is 2025, not the year AI solves markets. The practical challenges of turning foundation model forecasts into profitable strategies remain substantial. GARCH and ARIMA aren’t obsolete; they’re complementary. The key is understanding when each approach adds value. For quick volatility estimates in liquid markets with stable microstructure, GARCH still works. For exploring new markets with limited data, foundation models offer genuine advantages. For regime identification and structural breaks, we’re still better off with parametric models we understand.

What excites me most is the synthetic data generation capability. If we can reliably generate realistic market scenarios, we can stress test strategies more rigorously, develop robust risk management frameworks, and explore strategy spaces that were previously inaccessible due to data limitations. That’s genuinely new. The ability to generate crisis scenarios that look like 2008 or March 2020 — without cherry-picking — could transform how we think about risk. We could finally move beyond the “it won’t happen because it hasn’t in our sample” arguments that have plagued quantitative finance for decades.

But even here, caution is warranted. Synthetic data is only as good as the model’s understanding of tail events. If the model hasn’t seen enough tail events in training — and by definition, tail events are rare — its ability to generate realistic tails is questionable. The saying “garbage in, garbage out” applies to synthetic data generation as much as anywhere else.

The broader foundation model approach to time series — whether through Kronos, TimesFM, Lag-Llama, or the models yet to come — is worth serious attention. These are not magic bullets, but they represent a meaningful evolution in our methodological toolkit. For quants willing to learn new approaches while maintaining skepticism about hype, the next few years offer real opportunity. The question isn’t whether foundation models will matter for quant finance; it’s how quickly they can be integrated into production workflows in a way that’s robust, interpretable, and economically valuable.

I’m keeping an open mind while holding firm on skepticism. That’s served me well in 25 years of quantitative finance. It will serve us well here too.

Author’s Assessment: Bull Case vs. Bear Case

The Bull Case: Kronos demonstrates that large-scale domain-specific pre-training on financial data extracts genuinely transferable knowledge. The zero-shot performance on unseen markets is real — a model that’s never seen a particular futures contract can still generate reasonable volatility forecasts. For new market entry, cross-asset correlation modelling, and synthetic scenario generation, this is genuinely valuable. The synthetic data capability alone could transform backtesting robustness, letting us stress-test strategies against crisis scenarios that occur once every 20 years without waiting for history to repeat.

The Bear Case: The paper benchmarks on MSE and CRPS — statistical metrics, not economic ones. A model that improves next-candle MSE by 5% may have an information coefficient of 0.01 — statistically detectable at 12 billion observations but worthless after bid-ask spreads. More fundamentally, training on 12 billion samples of approximately-IID noise teaches the model the shape of noise, not exploitable alpha. The pre-training captures volatility clustering (a risk characteristic), not conditional mean predictability (an alpha characteristic). GARCH does the former with two parameters and full transparency; Kronos does it with millions of parameters and a black box. Show me a backtest with realistic execution costs before calling this a trading signal.

The Bottom Line: Kronos is a promising research direction, not a production alpha engine. The most defensible near-term value is in synthetic data augmentation for stress testing — a workflow enhancement, not a signal source. Build institutional familiarity, run controlled pilots, but don’t deploy for live trading until someone demonstrates economically exploitable returns after costs. The foundation model paradigm is directionally correct; the empirical evidence for direct alpha generation remains unproven.

Hands-On: Kronos vs GARCH

Let’s test the sidebar’s claim directly. We’ll fit a GARCH(1,1) to the same futures data and compare its volatility forecast to what Chronos produces:

import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
from arch import arch_model
from chronos import ChronosPipeline

# Fetch data
data = yf.download("ES=F", period="1y", progress=False)
returns = data['Close'].pct_change().dropna() * 100

# Split: use 80% for fitting, 20% for testing
split = int(len(returns) * 0.8)
train, test = returns[:split], returns[split:]

# GARCH(1,1) forecast
garch = arch_model(train, vol='Garch', p=1, q=1, dist='normal')
garch_fit = garch.fit(disp='off')
garch_forecast = garch_fit.forecast(horizon=len(test)).variance.iloc[-1].values

# Chronos forecast
pipeline = ChronosPipeline.from_pretrained("amazon/chronos-t5-large", device_map="cuda")
chronos_preds = pipeline.predict(train.values, prediction_length=len(test))
chronos_forecast = np.std(chronos_preds, axis=0) # Volatility as std dev

# MSE comparison
garch_mse = np.mean((garch_forecast - test.values**2)**2)
chronos_mse = np.mean((chronos_forecast - test.values**2)**2)

print(f"GARCH MSE: {garch_mse:.4f}")
print(f"Chronos MSE: {chronos_mse:.4f}")

# Plot
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(test.index, test.values**2, label="Realized", color="black", alpha=0.7)
ax.plot(test.index, garch_forecast, label="GARCH", color="blue")
ax.plot(test.index, chronos_forecast, label="Chronos", color="orange")
ax.set_title("Volatility Forecast: GARCH vs Foundation Model")
ax.legend()
plt.tight_layout()
plt.show()

Volatility Forecast Comparison: GARCH(1,1) vs Chronos Foundation Model

The bear case isn’t wrong: GARCH does volatility with 2 interpretable parameters and transparent assumptions. The foundation model uses millions of parameters. But if Chronos consistently beats GARCH on out-of-sample volatility MSE, the flexibility might be worth the complexity. Try running this yourself — the answer depends on the regime.

August 5, 2023

Pricing Options Using Machine Learning Algorithms

Pricing-Options-Using-Machine-Learning-Algorithms Download

January 29, 2023January 29, 2023

Trading Anomalies

An extract from my new book, Equity Analytics.

Trading-Anomalies-2

August 22, 2022August 22, 2022

Forecasting Market Indices Using Stacked Autoencoders & LSTM

Quality Research vs. Poor Research

The stem paper for this post is:

Bao W, Yue J, Rao Y (2017) A deep learning framework for financial time series using
stacked autoencoders and long-short term memory. PLoS ONE 12(7): e0180944. https://doi.org/10.1371/journal.pone.0180944

The chief claim by the researchers is that 90% to 95% 1-day ahead forecast accuracy can be achieved for a selection of market indices, including the S&P500 and Dow Jones Industrial Average, using a deep learning network of stacked autoencoders and LSTM layers, acting on data transformed using the Haar Discrete Wavelet Transform. The raw data comprises daily data for the index, around a dozen standard technical indicators, the US dollar index and an interest rate series.

Before we go into any detail let’s just step back and look at the larger picture. We have:

Unknown researchers
A journal from outside the field of finance
A paper replete with pretty colored images, but very skimpy detail on the methodology
A claimed result that lies far beyond the bounds of credibility

There’s enough red flags here to start a stampede at Pamplona. Let’s go through them one by one:

Everyone is unknown at some point in their career. But that’s precisely why you partner with a widely published author. It gives the reader confidence that the paper isn’t complete garbage.
Not everyone gets to publish in the Journal of Finance. I get that. How many of us were regular readers of the Journal of Political Economy before Black and Scholes published their famous paper on option pricing in 1973? Nevertheless, a finance paper published in a medical journal does not inspire great confidence.
Read almost any paper by a well known researcher and you will find copious detail on the methodology. These days, the paper is often accompanied by a Git repo (add 3 stars for this!). Academics producing quality research want readers to be able to replicate and validate their findings.
In this paper there are lots of generic, pretty colored graphics of deep learning networks, but no code repo and very little detail on the methodology. If you don’t want to publish details because the methodology is proprietary and potentially valuable, then do what I do: don’t publish at all.
One-day ahead forecasting accuracy of 53%-55% is good (52%-53% in HFT). 60% accuracy is outstanding. 90% – 95% is unbelievable. It’s a license to print money. So what we are being asked to believe is through a combination of data smoothing (which is all DWT is), dimensionality reduction (stacked autoencoders) and long-memory modeling, we can somehow improve forecasting accuracy over, say, a gradient boosted tree baseline, by something like 40%. It simply isn’t credible.

These simple considerations should be enough for any experienced quant to give the paper a wide berth.

Digging into the Methodology

Discrete Wavelet Transform

So we start from a raw dataset with variables that closely match those described in the paper (see headers for details). Of course, I don’t know the parameter values they used for most of the technical indicators, but it possibly doesn’t matter all that much.

Note that I am applying DWT using the Haar wavelet twice: once to the original data and then again to the transformed data. This has the effect of filtering out higher frequency “noise” in the data, which is the object of the exercise. If follow this you will also see that the DWT actually adds noisy fluctuations to the US Dollar index and 13-Week TBill series. So these should be excluded from the de-noising process. You can see how the DWT denoising process removes some of the higher frequency fluctuations from the opening price, for instance:

2. Stacked Autoencoders

First up, we need to produce data for training, validation and testing. I am doing this for just the first batch of data. We would then move the window forward + 3 months, rinse and repeat.

Note that:

(1) The data is being standardized. If you don’t do this the outputs from the autoencoders is mostly just 1s and 0s. Same happens if you use Min/Max scaling.

(2) We use the mean and standard deviation from the training dataset to normalize the test dataset. This is a trap that too many researchers fall into – standardizing the test dataset using the mean and standard deviation of the test dataset is feeding forward information.

The Autoencoder stack uses a hidden layer of size 10 in each encoder. We strip the output layer from the first encoder and use the hidden layer as inputs to the second autoencoder, and so on:

3. Benchmark Model

Before we plow on any further lets do a sanity check. We’ll use the Predict function to see if we’re able to get any promising-looking results. Here we are building a Gradient Boosted Trees predictor that maps the autoencoded training data to the corresponding closing prices of the index, one step ahead.

Next we use the predictor on the test dataset to produce 1-step-ahead forecasts for the closing price of the index.

Finally, we construct a trading model, as described in the paper, in which we go long or short the index depending on whether the forecast is above or below the current index level. The results do not look good (see below).

Now, admittedly, an argument can be made that a properly constructed LSTM model would outperform a simple gradient-boosted tree – but not by the amount that would be required to improve the prediction accuracy from around 50% to nearer 95%, the level claimed in the paper. At most I would expect to see a 1% to 5% improvement in forecast accuracy.

So what this suggests to me is that the researchers have got something wrong, by somehow allowing forward information to leak into the modeling process. The most likely culprits are:

Applying DWT transforms to the entire dataset, instead of the training and test sets individually
Standardzing the test dataset using the mean and standard deviation of the test dataset, instead of the training data set

A More Complete Attempt to Replicate the Research

There’s a much more complete attempt at replicating the research in this Git repo

As the repo author writes:

My attempts haven’t been succesful so far. Given the very limited comments regarding implementation in the article, it may be the case that I am missing something important, however the results seem too good to be true, so my assumption is that the authors have a bug in their own implementation. I would of course be happy to be proven wrong about this statement 😉

Conclusion

Over time, as one’s experience as a quant deepens, you learn to recognize the signs of shoddy research and save yourself the effort of trying to replicate it. It’s actually easier these days for researchers to fool themselves (and their readers) that they have uncovered something interesting, because of the facility with which complex algorithms can be deployed in an inappropriate way.

Postscript

This paper echos my concerns about the incorrect use of wavelets in a forecasting context:

The incorrect development of these wavelet-based forecasting models occurs during wavelet decomposition (the process of extracting high- and low-frequency information into different sub-time series known as wavelet and scaling coefficients, respectively) and as a result introduces error into the forecast model inputs. The source of this error is due to the boundary condition that is associated with wavelet decomposition (and the wavelet and scaling coefficients) and is linked to three main issues: 1) using ‘future data’ (i.e., data from the future that is not available); 2) inappropriately selecting decomposition levels and wavelet filters; and 3) not carefully partitioning calibration and validation data.

May 23, 2021May 25, 2021

Machine Learning Based Statistical Arbitrage

I have written extensively about statistical arbitrage strategies in previous posts, for example:

Successful Statistical Arbitrage

Developing Statistical Arbitrage Strategies Using Cointegration

Pairs Trading with Copulas

Applying Machine Learning in Statistical Arbitrage

In this series of posts I want to focus on applications of machine learning in stat arb and pairs trading, including genetic algorithms, deep neural networks and reinforcement learning.

Pair Selection

Let’s begin with the subject of pairs selection, to set the scene. The way this is typically handled is by looking at historical correlations and cointegration in a large universe of pairs. But there are serious issues with this approach, as described in this post:

Cointegration Breakdown

Instead I use a metric that I call the correlation signal, which I find to be a more reliable indicator of co-movement in the underlying asset processes. I wont delve into the details here, but you can get the gist from the following:

The search algorithm considers pairs in the S&P 500 membership and ranks them in descending order of correlation information. Pairs with the highest values (typically of the order of 100, or greater) tend to be variants of the same underlying stock, such as GOOG vs GOOGL, which is an indication that the metric “works” (albeit that such pairs offer few opportunities at low frequency). The pair we are considering here has a correlation signal value of around 14, which is also very high indeed.

Trading Strategy Development

We begin by collecting five years of returns series for the two stocks:

The first approach we’ll consider is the unadjusted spread, being the difference in returns between the two series, from which we crate a normalized spread “price”, as follows.

This methodology is frowned upon as the resultant spread is unlikely to be stationary, as you can see for this example in the above chart. But it does have one major advantage in terms of implementation: the same dollar value is invested in both long and short legs of the spread, making it the most efficient approach in terms of margin utilization and capital cost – other approaches entail incurring an imbalance in the dollar value of the two legs.

But back to nonstationarity. The problem is that our spread price series looks like any other asset price process – it trends over long periods and tends to wander arbitrarily far from its starting point. This is NOT the outcome that most statistical arbitrageurs are looking to achieve. On the contrary, what they want to see is a stationary process that will tend to revert to its mean value whenever it moves too far in one direction.

Still, this doesn’t necessarily determine that this approach is without merit. Indeed, it is a very typical trading strategy amongst futures traders for example, who are often looking for just such behavior in their trend-following strategies. Their argument would be that futures spreads (which are often constructed like this) exhibit clearer, longer lasting and more durable trends than in the underlying futures contracts, with lower volatility and market risk, due to the offsetting positions in the two legs. The argument has merit, no doubt. That said, spreads of this kind can nonetheless be extremely volatile.

So how do we trade such a spread? One idea is to add machine learning into the mix and build trading systems that will seek to capitalize on long term trends. We can do that in several ways, one of which is to apply genetic programming techniques to generate potential strategies that we can backtest and evaluate. For more detail on the methodology, see:

A Primer on Genetic Programming

I built an entire hedge fund using this approach in the early 2000’s (when machine learning was entirely unknown to the general investing public). These days there are some excellent software applications for generating trading systems and I particularly like Mike Bryant’s Adaptrade Builder, which was used to create the strategies shown below:

Builder has no difficulty finding strategies that produce a smooth equity curve, with decent returns, low drawdowns and acceptable Sharpe Ratios and Profit Factors – at least in backtest! Of course, there is a way to go here in terms of evaluating such strategies and proving their robustness. But it’s an excellent starting point for further R&D.

But let’s move on to consider the “standard model” for pairs trading. The way this works is that we consider a linear model of the form

Y(t) = beta * X(t) + e(t)

Where Y(t) is the returns series for stock 1, X(t) is the returns series in stock 2, e(t) is a stationary random error process and beta (is this model) is a constant that expresses the linear relationship between the two asset processes. The idea is that we can form a spread process that is stationary:

Y(t) – beta * X(t) = e(t)

In this case we estimate beta by linear regression to be 0.93. The residual spread process has a mean very close to zero, and the spread price process remains within a range, which means that we can buy it when it gets too low, or sell it when it becomes too high, in the expectation that it will revert to the mean:

In this approach, “buying the spread” means purchasing shares to the value of, say, $1M in stock 1, and selling beta * $1M of stock 2 (around $930,000). While there is a net dollar imbalance in the dollar value of the two legs, the margin impact tends to be very small indeed, while the overall portfolio is much more stable, as we have seen.

The classical procedure is to buy the spread when the spread return falls 2 standard deviations below zero, and sell the spread when it exceeds 2 standard deviations to the upside. But that leaves a lot of unanswered questions, such as:

After you buy the spread, when should you sell it?
Should you use a profit target?
Where should you set a stop-loss?
Do you increase your position when you get repeated signals to go long (or short)?
Should you use a single, or multiple entry/exit levels?

And so on – there are a lot of strategy components to consider. Once again, we’ll let genetic programming do the heavy lifting for us:

What’s interesting here is that the strategy selected by the Builder application makes use of the Bollinger Band indicator, one of the most common tools used for trading spreads, especially when stationary (although note that it prefers to use the Opening price, rather than the usual close price):

Ok so far, but in fact I cheated! I used the entire data series to estimate the beta coefficient, which is effectively feeding forward-information into our model. In reality, the data comes at us one day at a time and we are required to re-estimate the beta every day.

Let’s approximate the real-life situation by re-estimating beta, one day at a time. I am using an expanding window to do this (i.e. using the entire data series up to each day t), but is also common to use a fixed window size to give a “rolling” estimate of beta in which the latest data plays a more prominent part in the estimation. The process now looks like this:

Here we use OLS to produce a revised estimate of beta on each trading day. So our model now becomes:

Y(t) = beta(t) * X(t) + e(t)

i.e. beta is now time-varying, as can be seen from the chart above.

The synthetic spread price appears to be stationary (we can test this), although perhaps not to the same degree as in the previous example, where we used the entire data series to estimate a single, constant beta. So we might anticipate that out ML algorithm would experience greater difficulty producing attractive trading models. But, not a bit of it – it turns out that we are able to produce systems that are just as high performing as before:

In fact this strategy has higher returns, Sharpe Ratio, Sortino Ratio and lower drawdown than many of the earlier models.

Conclusion

The purpose of this post was to show how we can combine the standard approach to statistical arbitrage, which is based on classical econometric theory, with modern machine learning algorithms, such as genetic programming. This frees us to consider a very much wider range of possible trade entry and exit strategies, beyond the rather simplistic approach adopted when pairs trading was first developed. We can deploy multiple trade entry levels and stop loss levels to manage risk, dynamically size the trade according to current market conditions and give emphasis to alternative performance characteristics such as maximum drawdown, or Sharpe or Sortino ratio, in addition to strategy profitability.

The programatic nature of the strategies developed in the way also make them very amenable to optimization, Monte Carlo simulation and stress testing.

This is but one way of adding machine learning methodologies to the mix. In a series of follow-up posts I will be looking at the role that other machine learning techniques – such as deep learning and reinforcement learning – can play in improving the performance characteristics of the classical statistical arbitrage strategy.

November 24, 2020

Can Machine Learning Techniques Be Used To Predict Market Direction? The 1,000,000 Model Test.

During the 1990’s the advent of Neural Networks unleashed a torrent of research on their applications in financial markets, accompanied by some rather extravagant claims about their predicative abilities. Sadly, much of the research proved to be sub-standard and the results illusionary, following which the topic was largely relegated to the bleachers, at least in the field of financial market research.

With the advent of new machine learning techniques such as Random Forests, Support Vector Machines and Nearest Neighbor Classification, there has been a resurgence of interest in non-linear modeling techniques and a flood of new research, a fair amount of it supportive of their potential for forecasting financial markets. Once again, however, doubts about the quality of some of the research bring the results into question.

Against this background I and my co-researcher Dan Rico set out to address the question of whether these new techniques really do have predicative power, more specifically the ability to forecast market direction. Using some excellent MatLab toolboxes and a new software package, an Excel Addin called 11Ants, that makes large scale testing of multiple models a snap, we examined over 1,000,000 models and model-ensembles, covering just about every available non-linear technique. The data set for our study comprised daily prices for a selection of US equity securities, together with a large selection of technical indicators for which some other researchers have claimed explanatory power.

In-Sample Equity Curve for Best Performing Nonlinear Model

The answer provided by our research was, without exception, in the negative: not one of the models tested showed any significant ability to predict the direction of any of the securities in our data set. Furthermore, our study found that the best-performing models favored raw price data over technical indicator variables, suggesting that the latter have little explanatory power.

As with Neural Networks, the principal difficulty with non-linear techniques appears to be curve-fitting and a failure to generalize: while it is very easy to find models that provide an excellent fit to in-sample data, the forecasting performance out-of-sample is often very poor.

Out-of-Sample Equity Curve for Best Performing Nonlinear Model

Some caveats about our own research apply. First and foremost, it is of course impossible to prove a hypothesis in the negative. Secondly, it is plausible that some markets are less efficient than others: some studies have claimed success in developing predictive models due to the (relative) inefficiency of the F/X and futures markets, for example. Thirdly, the choice of sample period may be criticized: it could be that the models were over-conditioned on a too- lengthy in-sample data set, which in one case ran from 1993 to 2008, with just two years (2009-2010) of out-of-sample data. The choice of sample was deliberate, however: had we omitted the 2008 period from the “learning” data set, it would be very easy to criticize the study for failing to allow the algorithms to learn about the exceptional behavior of the markets during that turbulent year.

Despite these limitations, our research casts doubt on the findings of some less-extensive studies, that may be the result of sample-selection bias. One characteristic of the most credible studies finding evidence in favor of market predictability, such as those by Pesaran and Timmermann, for instance (see paper for citations), is that the models they employ tend to incorporate independent explanatory variables, such as yield spreads, which do appear to have real explanatory power. The finding of our study suggest that, absent such explanatory factors, the ability to predict markets using sophisticated non-linear techniques applied to price data alone may prove to be as illusionary as it was in the 1990’s.

ONE MILLION MODELS

May 12, 2020May 12, 2020

Systematic Futures Trading

In its proprietary trading, Systematic Strategies primary focus in on equity and volatility strategies, both low and high frequency. In futures, the emphasis is on high frequency trading, although we also run one or two lower frequency strategies that have higher capacity, such as the Futures WealthBuilder. The version of WealthBuilder running on the Collective 2 site has performed very well in 2017, with net returns of 30% and a Sharpe Ratio of 3.4:

In the high frequency space, our focus is on strategies with very high Sharpe Ratios and low drawdowns. We trade a range of futures products, including equity, fixed income, metals and energy markets. Despite the current low levels of market volatility, these strategies have performed well in 2017:

Building high frequency strategies with double-digit Sharpe Ratios requires a synergy of computational capability and modeling know-how. The microstructure of futures markets is, of course, substantially different to that of equity or forex markets and the components of the model that include microstructure effects vary widely from one product to another. There can be substantial variations too in the way that time is handled in the model – whether as discrete or continuous “wall time”, in trade time, or some other measure. But some of the simple technical indicators we use – moving averages, for example – are common to many models across different products and markets. Machine learning plays a role in most of our trading strategies, including high frequency.

Here are some relevant blog posts that you may find interesting:

http://jonathankinlay.com/2016/04/high-frequency-trading-equities-vs-futures/

http://jonathankinlay.com/2015/05/designing-scalable-futures-strategy/

http://jonathankinlay.com/2014/10/day-trading-system-in-vix-futures/

April 28, 2020

A Winer Process

No doubt many of you sharp-eyed readers will have spotted a spelling error, thinking I intended to refer to one of these:

But, in fact, I really did have in mind something more like this:

We are following an example from the recently published Mathematica Beyond Mathematics by Jose Sanchez Leon, an up-to-date text that describes many of the latest features in Mathematica, illustrated with interesting applications. Sanchez Leon shows how Mathematica’s machine learning capabilities can be applied to the craft of wine-making.

We begin by loading a curated Wolfram dataset comprising measurements of the physical properties and quality of wines:

A Machine Learning Prediction Model for Wine Quality

We’re going to apply Mathematica’s built-in machine learning algorithms to train a predictor of wine quality, using the training dataset. Mathematica determines that the most effective machine learning technique in this case is Random Forest and after a few seconds produces the predictor function:

Mathematica automatically selects what it considers to be the best performing model from several available machine learning algorithms:

Let’s take a look at how well the predictor perform on the test dataset of 1,298 wines:

We can use the predictor function to predict the quality of an unknown wine, based on its physical properties:

Next we create a function to predict the quality of an unknown wine as a function of just two of its characteristics, its pH and alcohol level. The analysis suggests that the quality of our unknown wine could be improved by increasing both its pH and alcohol content:

Applications and Examples

This simple toy example illustrates how straightforward it is to deploy machine learning techniques in Mathematica. Machine Learning and Neural Networks became a major focus for Wolfram Research in version 10, and the software’s capabilities have been significantly enhanced in version 11, with several applications such as text and sentiment analysis that have direct relevance to trading system development:

For other detailed examples see:

http://jonathankinlay.com/2016/08/machine-learning-model-spy/

http://jonathankinlay.com/2016/11/trading-market-sentiment/

http://jonathankinlay.com/2016/08/dynamic-time-warping/

April 21, 2020

The Story of a HFT Strategy

VIX HFT Scalper