Money Management Archives - QUANTITATIVE RESEARCH AND TRADING

May 21, 2019

High Frequency Trading: Equities vs. Futures

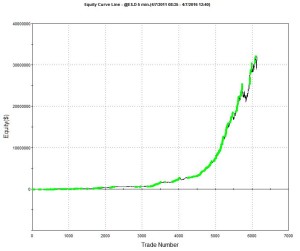
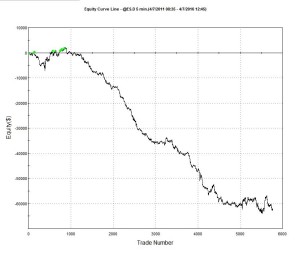
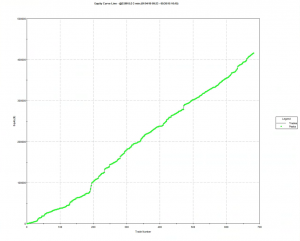
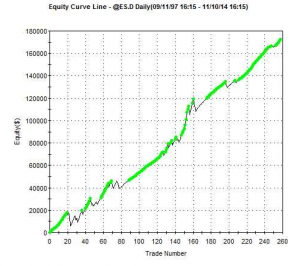
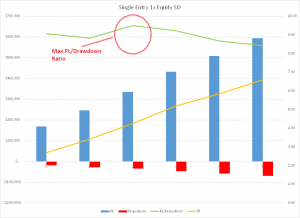
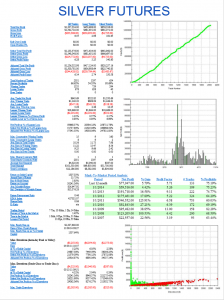
A talented young system developer I know recently reached out to me with an interesting-looking equity curve for a high frequency strategy he had designed in E-mini futures:

Pretty obviously, he had been making creative use of the “money management” techniques so beloved by futures systems designers. I invited him to consider how it would feel to be trading a 1,000-lot E-mini position when the market took a 20 point dive. A $100,000 intra-day drawdown might make the strategy look a little less appealing. On the other hand, if you had already made millions of dollars in the strategy, you might no longer care so much.

A more important criticism of money management techniques is that they are typically highly path-dependent: if you had started your strategy slightly closer to one of the drawdown periods that are almost unnoticeable on the chart, it could have catastrophic consequences for your trading account. The only way to properly evaluate this, I advised, was to backtest the strategy over many hundreds of thousands of test-runs using Monte Carlo simulation. That would reveal all too clearly that the risk of ruin was far larger than might appear from a single backtest.

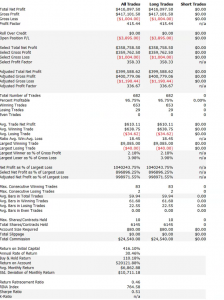
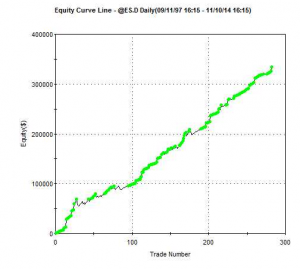
Next, I asked him whether the strategy was entering and exiting passively, by posting bids and offers, or aggressively, by crossing the spread to sell at the bid and buy at the offer. I had a pretty good idea what his answer would be, given the volume of trades in the strategy and, sure enough he confirmed the strategy was using passive entries and exits. Leaving to one side the challenge of executing a trade for 1,000 contracts in this way, I instead ask him to show me the equity curve for a single contract in the underlying strategy, without the money-management enhancement. It was still very impressive.

The Critical Fill Assumptions For Passive Strategies

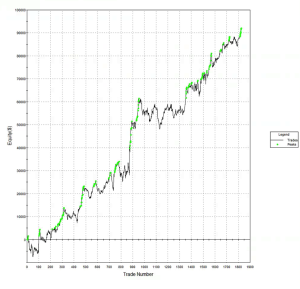
But there is an underlying assumption built into these results, one that I have written about in previous posts: the fill rate. Typically in a retail trading platform like Tradestation the assumption is made that your orders will be filled if a trade occurs at the limit price at which the system is attempting to execute. This default assumption of a 100% fill rate is highly unrealistic. The system’s orders have to compete for priority in the limit order book with the orders of many thousands of other traders, including HFT firms who are likely to beat you to the punch every time. As a consequence, the actual fill rate is likely to be much lower: 10% to 20%, if you are lucky. And many of those fills will be “toxic”: buy orders will be the last to be filled just before the market moves lower and sell orders will be the last to get filled just as the market moves higher. As a result, the actual performance of the strategy will be a very long way from the pretty picture shown in the chart of the hypothetical equity curve.

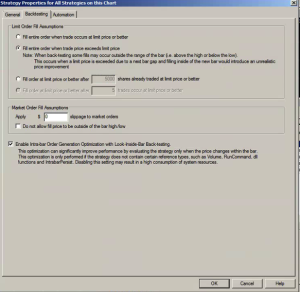
One way to get a handle on the problem is to make a much more conservative assumption, that your limit orders will only get filled when the market moves through them. This can easily be achieved in a product like Tradestation by selecting the appropriate backtest option:

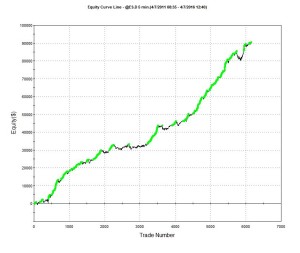
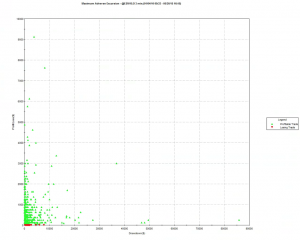
The strategy performance results often look very different when this much more conservative fill assumption is applied. The outcome for this system was not at all unusual:

Of course, the more conservative assumption applied here is also unrealistic: many of the trading system’s sell orders would be filled at the limit price, even if the market failed to move higher (or lower in the case of a buy order). Furthermore, even if they were not filled during the bar-interval in which they were issued, many limit orders posted by the system would be filled in subsequent bars. But the reality is likely to be much closer to the outcome assuming a conservative fill-assumption than an optimistic one. Put another way: if the strategy demonstrates good performance under both pessimistic and optimistic fill assumptions there is a reasonable chance that it will perform well in practice, other considerations aside.

An Example of a HFT Equity Strategy

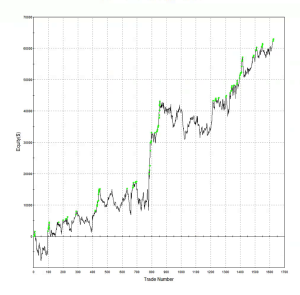
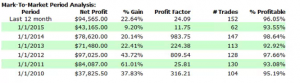
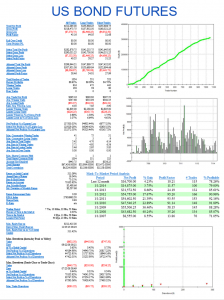
Let’s contrast the futures strategy with an example of a similar HFT strategy in equities. Under the optimistic fill assumption the equity curve looks as follows:

Under the more conservative fill assumption, the equity curve is obviously worse, but the strategy continues to produce excellent returns. In other words, even if the market moves against the system on every single order, trading higher after a sell order is filled, or lower after a buy order is filled, the strategy continues to make money.

Market Microstructure

There is a fundamental reason for the discrepancy in the behavior of the two strategies under different fill scenarios, which relates to the very different microstructure of futures vs. equity markets. In the case of the E-mini strategy the average trade might be, say, $50, which is equivalent to only 4 ticks (each tick is worth $12.50). So the average trade: tick size ratio is around 4:1, at best. In an equity strategy with similar average trade the tick size might be as little as 1 cent. For a futures strategy, crossing the spread to enter or exit a trade more than a handful of times (or missing several limit order entries or exits) will quickly eviscerate the profitability of the system. A HFT system in equities, by contrast, will typically prove more robust, because of the smaller tick size.

Of course, there are many other challenges to high frequency equity trading that futures do not suffer from, such as the multiplicity of trading destinations. This means that, for instance, in a consolidated market data feed your system is likely to see trading opportunities that simply won’t arise in practice due to latency effects in the feed. So the profitability of HFT equity strategies is often overstated, when measured using a consolidated feed. Futures, which are traded on a single exchange, don’t suffer from such difficulties. And there are a host of other differences in the microstructure of futures vs equity markets that the analyst must take account of. But, all that understood, in general I would counsel that equities make an easier starting point for HFT system development, compared to futures.

November 27, 2018

Designing a Scalable Futures Strategy

I have been working on a higher frequency version of the eMini S&P 500 futures strategy, based on 3-minute bar intervals, which is designed to trade a couple of times a week, with hold periods of 2-3 days. Even higher frequency strategies are possible, of course, but my estimation is that a hold period of under a week provides the best combination of liquidity and capacity. Furthermore, the strategy is of low enough frequency that it is not at all latency sensitive – indeed, in the performance analysis below I have assumed that the market must trade through the limit price before the system enters a trade (relaxing the assumption and allowing the system to trade when the market touches the limit price improves the performance).

The other important design criteria are the high % of profitable trades and Kelly f (both over 95%). This enables the investor to employ money management techniques, such a fixed-fractional allocation for example, in order to scale the trade size up from 1 to 10 contracts, without too great a risk of a major drawdown in realized P&L.

The end result is a strategy that produces profits of $80,000 to $100,000 a year on a 10 contract position, with an annual rate of return of 30% and a Sharpe ratio in excess of 2.0.

Furthermore, of the 682 trades since Jan 2010, only 29 have been losers.

Annual P&L (out of sample)

Equity Curve

Strategy Performance

What’s the Downside?

Everything comes at a price, of course. Firstly, the strategy is long-only and, by definition, will perform poorly in falling markets, such as we saw in 2008. That’s a defensible investment thesis, of course – how many $billions are invested in buy and hold strategies? – and, besides, as one commentator remarked, the trick is to develop multiple strategies for different market regimes (although, sensible as that sounds, one is left with the difficulty of correctly identifying the market regime).

The second drawback is revealed by the trade chart below, which plots the drawdown experienced during each trade. The great majority of these drawdowns are unrealized, and in most cases the trade recovers to make a profit. However, there are some very severe cases, such as Sept 2014, when the strategy experienced a drawdown of $85,000 before recovering to make a profit on the trade. For most investors, the agony of risking an entire year’s P&L just to make a few hundred dollars would be too great.

It should be pointed out that the by the time the drawdown event took place the strategy had already produced many hundreds of thousands of dollars of profit. So, one could take the view that by that stage the strategy was playing with “house money” and could well afford to take such a risk.

One obvious “solution” to the drawdown problem is to use some kind of stop loss. Unfortunately, the effect is simply to convert an unrealized drawdown into a realized loss. For some, however, it might be preferable to take a hit of $40,000 or $50,000 once every few years, rather than suffer the uncertainty of an even larger potential loss. Either way, despite its many pleasant characteristics, this is not a strategy for investors with weak stomachs!

September 23, 2018

Money Management – the Good, the Bad and the Ugly

The infatuation of futures traders with the subject of money management, (more aptly described as position sizing), is something of a puzzle for someone coming from a background in equities or forex. The idea is, simply, that one can improve one’s trading performance through the judicious use of leverage, increasing the size of a position at times and reducing it at others.

Perhaps the most widely known money management technique is the Martingale, where the size of the trade is doubled after every loss. It is easy to show mathematically that such a system must win eventually, provided that the bet size is unlimited. It is also easy to show that, small as it may be, there is a non-zero probability of a long string of losing trades that would bankrupt the trader before he was able to recoup all his losses. Still, the prospect offered by the Martingale strategy is an alluring one: the idea that, no matter what the underlying trading strategy, one can eventually be certain of winning. And so a virtual cottage industry of money management techniques has evolved.

One of the reasons why the money management concept is prevalent in the futures industry compared to, say, equities or f/x, is simply the trading mechanics. Doubling the size of a position in futures might mean trading an extra contract, or perhaps a ten-lot; doing the same in equities might mean scaling into and out of multiple positions comprising many thousands of shares. The execution risk and cost of trying to implement a money management program in equities has historically made the idea infeasible, although that is less true today, given the decline in commission rates and the arrival of smart execution algorithms. Still, money management is a concept that originated in the futures industry and will forever be associated with it.

Van Tharp on Position Sizing
I was recently recommended to read Van Tharp’s Definitive Guide to Position Sizing, which devotes several hundred pages to the subject. Leaving aside the great number of pages of simulation results, there is much to commend it. Van Tharp does a pretty good job of demolishing highly speculative and very dangerous “money management” techniques such as the Kelly Criterion and Ralph Vince’s Optimal f, which make unrealistic assumptions of one kind or another, such as, for example, that there are only two outcomes, rather than the multiple possibilities from a trading strategy, or considering only the outcome of a single trade, rather than a succession of trades (whose outcome may not be independent). Just as with the Martingale, these techniques will often produce unacceptably large drawdowns. In fact, as I have pointed out elsewhere, the use of leverage which many so-called money management techniques actually calls for increases in the risk in the original strategy, often reducing its risk-adjusted return.

As Van Tharp points out, mathematical literacy is not one of the strongest suits of futures traders in general and the money management strategy industry reflects that.

But Van Tharp himself is not immune to misunderstanding mathematical concepts. His central idea is that trading systems should be rated according to its System Quality Number, which he defines as:

SQN = (Expectancy / standard deviation of R) * square root of Number of Trades

R is a central concept of Van Tharp’s methodology, which he defines as how much you will lose per unit of your investment. So, for example, if you buy a stock today for $50 and plan to sell it if it reaches $40, your R is $10. In cases like this you have a clear definition of your R. But what if you don’t? Van Tharp sensibly recommends you use your average loss as an estimate of R.

Expectancy, as Van Tharp defines it, is just the expected profit per trade of the system expressed as a multiple of R. So

SQN = ( (Average Profit per Trade / R) / standard deviation (Average Profit per Trade / R) * square root of Number of Trades

Squaring both sides of the equation, we get:

SQN^2 = ( (Average Profit per Trade )^2 / R^2) / Variance (Average Profit per Trade / R) ) * Number of Trades

The R-squared terms cancel out, leaving the following:

SQN^2 = ((Average Profit per Trade ) ^ 2 / Variance (Average Profit per Trade)) * Number of Trades

Hence,

SQN = (Average Profit per Trade / Standard Deviation (Average Profit per Trade)) * square root of Number of Trades

There is another name by which this measure is more widely known in the investment community: the Sharpe Ratio.

On the “Optimal” Position Sizing Strategy
In my view, Van Tharp’s singular achievement has been to spawn a cottage industry out of restating a fact already widely known amongst investment professionals, i.e. that one should seek out strategies that maximize the Sharpe Ratio.

Not that seeking to maximize the Sharpe Ratio is a bad idea – far from it. But then Van Tharp goes on to suggest that one should consider only strategies with a SQN of greater than 2, ideally much higher (he mentions SQNs of the order of 3-6).

But 95% or more of investable strategies have a Sharpe Ratio less than 2. In fact, in the world of investment management a Sharpe Ratio of 1.5 is considered very good. Barely a handful of funds have demonstrated an ability to maintain a Sharpe Ratio of greater than 2 over a sustained period (Jim Simon’s Renaissance Technologies being one of them). Only in the world of high frequency trading do strategies typically attain the kind of Sharpe Ratio (or SQN) that Van Tharp advocates. So while Van Tharp’s intentions are well meaning, his prescription is unrealistic, for the majority of investors.

One recommendation of Van Tharp’s that should be taken seriously is that there is no single “best” money management strategy that suits every investor. Instead, position sizing should be evolved through simulation, taking into account each trader or investor’s preferences in terms of risk and return. This makes complete sense: a trader looking to make 100% a year and willing to risk 50% of his capital is going to adopt a very different approach to money management, compared to an investor who will be satisfied with a 10% return, provided his risk of losing money is very low. Again, however, there is nothing new here: the problem of optimal allocation based on an investor’s aversion to risk has been thoroughly addressed in the literature for at least the last 50 years.

What about the Equity Curve Money Management strategy I discussed in a previous post? Isn’t that a kind of Martingale? Yes and no. Indeed, the strategy does require us to increase the original investment after a period of loss. But it does so, not after a single losing trade, but after a series of losses from which the strategy is showing evidence of recovering. Furthermore, the ECMM system caps the add-on investment at some specified level, rather than continuing to double the trade size after every loss, as in a Martingale.

But the critical difference between the ECMM and the standard Martingale lies in the assumptions about dependency in the returns of the underlying strategy. In the traditional Martingale, profits and losses are independent from one trade to the next. By contrast, scenarios where ECMM is likely to prove effective are ones where there is dependency in the underlying strategy, more specifically, negative autocorrelation in returns over some horizon. What that means is that periods of losses or lower returns tend to be followed by periods of gains, or higher returns. In other words, ECMM works when the underlying strategy has a tendency towards mean reversion.

CONCLUSION
The futures industry has spawned a myriad of position sizing strategies. Many are impractical, or positively dangerous, leading as they do to significant risk of catastrophic loss. Generally, investors should seek out strategies with higher Sharpe Ratios, and use money management techniques only to improve the risk-adjusted return. But there is no universal money management methodology that will suit every investor. Instead, money management should be conditioned on each individual investors risk preferences.

September 22, 2018

Equity Curve Money Management

Amongst a wide variety of money management methods that have evolved over the years, a perennial favorite is the use of the equity curve to guide position sizing. The most common version of this technique is to add to the existing position (whether long or short) depending on the relationship between the current value of the account equity (realized + unrealized PL) and its moving average. According to whether you believe that the equity curve is momentum driven, or mean reverting, you will add to your existing position when the equity move above (or, on the case of mean-reverting, below) the long term moving average.

In this article I want to discuss a slightly different version of equity curve money management, which is mean-reversion oriented. The underlying thesis is that your trading strategy has good profit characteristics, and while it suffers from the occasional, significant drawdown, it can be expected to recover from the downswings. You should therefore be looking to add to your positions when the equity curve moves down sufficiently, in the expectation that the trading strategy will recover. The extra contracts you add to your position during such downturns with increase the overall P&L. To illustrate the approach I am going to use a low frequency strategy on the S&P500 E-mini futures contract (ES). The performance of the strategy is summarized in the chart and table below.

(click to enlarge)

The overall results of the strategy are not bad: at over 87% the win rate is high as, too, is the profit factor of 2.72. And the strategy’s performance, although hardly stellar, has been quite consistent over the period from 1997. That said, most the profits derive from the long side, and the strategy suffers from the occasional large loss, including a significant drawdown of over 18% in 2000.

I am going to use this underlying strategy to illustrate how its performance can be improved with equity curve money management (ECMM). To start, we calculate a simple moving average of the equity curve, as before. However, in this variation of ECMM we then calculate offsets that are a number of standard deviations above or below the moving average. Typical default values for the moving average length might be 50 bars for a daily series, while we might use, say, +/- 2 S.D. above and below the moving average as our trigger levels. The idea is that we add to our position when the equity curve falls below the lower threshold level (moving average – 2x S.D) and then crosses back above it again. This is similar to how a trader might use Bollinger bands, or an oscillator like Stochastics. The chart below illustrates the procedure.

The lower and upper trigger levels are shown as green and yellow lines in the chart indicator (note that in this variant of ECMM we only use the lower level to add to positions).

After a significant drawdown early in October the equity curve begins to revert and crosses back over the lower threshold level on Oct 21. Applying our ECMM rule, we add to our existing long position the next day, Oct 22 (the same procedure would apply to adding to short positions). As you can see, our money management trade worked out very well, since the EC did continue to mean-revert as expected. We closed the trade on Nov 11, for a substantial, additional profit.

Now we have illustrated the procedure, let’s being to explore the potential of the ECMM idea in more detail. The first important point to understand is what ECMM will NOT do: i.e. reduce risk. Like all money management techniques that are designed to pyramid into positions, ECMM will INCREASE risk, leading to higher drawdowns. But ECMM should also increase profits: so the question is whether the potential for greater profits is sufficient to offset the risk of greater losses. If not, then there is a simpler alternative method of increasing profits: simply increase position size! It follows that one of the key metrics of performance to focus on in evaluating this technique is the ratio of PL to drawdown. Let’s look at some examples for our baseline strategy.

The chart shows the effect of adding a specified number of contracts to our existing long or short position whenever the equity curve crosses back above the lower trigger level, which in this case is set at 2xS.D below the 50-day moving average of the equity curve. As expected, the overall strategy P&L increases linearly in line with the number of additional contracts traded, from a base level of around $170,000, to over $500,000 when we trade an additional five contracts. So, too, does the profit factor rise from around 2.7 to around 5.0. That’s where the good news ends. Because, just as the strategy PL increases, so too does the size of the maximum drawdown, from $(18,500) in the baseline case to over $(83,000) when we trade an additional five contracts. In fact, the PL/Drawdown ratio declines from over 9.0 in the baseline case, to only 6.0 when we trade the ECMM strategy with five additional contracts. In terms of risk and reward, as measured by the PL/Drawdown ratio, we would be better off simply trading the baseline strategy: if we traded 3 contracts instead of 1 contract, then without any money management at all we would have made total profits of around $500,000, but with a drawdown of just over $(56,000). This is the same profit as produced with the 5-contract ECMM strategy, but with a drawdown that is $23,000 smaller.

How does this arise? Quite simply, our ECMM money management trades as not all automatic winners from the get-go (even if they eventually produce profits. In some cases, having crossed above the lower threshold level, the equity curve will subsequently cross back down below it again. As it does so, the additional contracts we have traded are now adding to the strategy drawdown.

This suggests that there might be a better alternative. How about if, instead of doing a single ECMM trade for, say, 5 additional contracts, we instead add an additional contract each time the equity curve crosses above the lower threshold level. Sure, we might give up some extra profits, but our drawdown should be lower, right? That turns out to be true. Unfortunately, however, profits are impacted more than the drawdown, so as a result the PL/Drawdown ratio shows the same precipitous decline:

Once again, we would be better off trading the baseline strategy in larger size, rather than using ECMM, even when we scale into the additional contracts.

What else can we try? An obvious trick to try is tweaking the threshold levels. We can do this by adjusting the # of standard deviations at which to set the trigger levels. Intuitively, it might seem that the obvious thing to do is set the threshold levels further apart, so that ECMM trades are triggered less frequently. But, as it turns out, this does not produce the desired effect. Instead, counter-intuitively, we have to set the threshold levels CLOSER to the moving average, at only +/-1x S.D. The results are shown in the chart below.

With these settings, the strategy PL and profit factor increase linearly, as before. So too does the strategy drawdown, but at a slower rate. As a consequence, the PL/Drawdown ration actually RISES, before declining at a moderate pace. Looking at the chart, it is apparent the optimal setting is trading two additional contracts with a threshold setting one standard deviation below the 50-day moving average of the equity curve.

Below are the overall results. With these settings the baseline strategy plus ECMM produces total profits of $334,000, a profit factor of 4.27 and a drawdown of $(35,212), making the PL/Drawdown ratio 9.50. Producing the same rate of profits using the baseline strategy alone would require us to trade two contracts, producing a slightly higher drawdown of almost $(37,000). So our ECMM strategy has increased overall profitability on a risk-adjusted basis.

(Click to enlarge)

CONCLUSION

It is certainly feasible to improve not only the overall profitability of a strategy using equity curve money management, but also the risk-adjusted performance. Whether ECMM will have much effect depends on the specifics of the underlying strategy, and the level at which the ECMM parameters are set to. These can be optimized on a walk-forward basis.

EASYLANGUAGE CODE

Inputs:

MALen(50),
SDMultiple(2),
PositionMult(1),
ExitAtBreakeven(False);

Var:
OpenEquity(0),
EquitySD(0),
EquityMA(0),
UpperEquityLevel(0),
LowerEquityLevel(0),
NShares(0);

OpenEquity=OpenPositionProfit+NetProfit;a
EquitySD=stddev(OpenEquity,MALen);
EquityMA=average(OpenEquity,MALen);
UpperEquityLevel=EquityMA + SDMultiple*EquitySD;
LowerEquityLevel=EquityMA-SDMultiple*EquitySD;
NShares=CurrentContracts*PositionMult;
If OpenEquity crosses above LowerEquityLevel then begin
If Marketposition > 0 then begin
Buy(“EnMark-LMM”) NShares shares next bar at market;
end;
If Marketposition < 0 then begin
Sell Short(“EnMark-SMM”) NShares shares next bar at market;
end;
end;
If ExitAtBreakeven then begin

If OpenEquity crosses above EquityMA then begin
If Marketposition > 1 then begin
Sell Short (“ExBE-LMM”) (Currentcontracts-1) shares next bar at market;
end;
If Marketposition < -1 then begin
Buy (“ExBE-SMM”) (Currentcontracts-1) shares next bar at market;
end;

end;
end;

September 21, 2018

Building Systematic Strategies – A New Approach

Anyone active in the quantitative space will tell you that it has become a great deal more competitive in recent years. Many quantitative trades and strategies are a lot more crowded than they used to be and returns from existing strategies are on the decline.

THE CHALLENGE

Meanwhile, costs have been steadily rising, as the technology arms race has accelerated, with more money being spent on hardware, communications and software than ever before. As lead times to develop new strategies have risen, the cost of acquiring and maintaining expensive development resources have spiraled upwards. It is getting harder to find new, profitable strategies, due in part to the over-grazing of existing methodologies and data sets (like the E-Mini futures, for example). There has, too, been a change in the direction of quantitative research in recent years. Where once it was simply a matter of acquiring the fastest pipe to as many relevant locations as possible, the marginal benefit of each extra $ spent on infrastructure has since fallen rapidly. New strategy research and development is now more model-driven than technology driven.

THE OPPORTUNITY

What is needed at this point is a new approach: one that accelerates the process of identifying new alpha signals, prototyping and testing new strategies and bringing them into production, leveraging existing battle-tested technologies and trading platforms.

GENETIC PROGRAMMING

Genetic programming, which has been around since the 1990’s when its use was pioneered in proteomics, enjoys significant advantages over traditional research and development methodologies.

GP is an evolutionary-based algorithmic methodology in which a system is given a set of simple rules, some data, and a fitness function that produces desired outcomes from combining the rules and applying them to the data. The idea is that, by testing large numbers of possible combinations of rules, typically in the millions, and allowing the most successful rules to propagate, eventually we will arrive at a strategy solution that offers the required characteristics.

ADVANTAGES OF GENETIC PROGRAMMING

The potential benefits of the GP approach are considerable: not only are strategies developed much more quickly and cost effectively (the price of some software and a single CPU vs. a small army of developers), the process is much more flexible. The inflexibility of the traditional approach to R&D is one of its principle shortcomings. The researcher produces a piece of research that is subsequently passed on to the development team. Developers are usually extremely rigid in their approach: when asked to deliver X, they will deliver X, not some variation on X. Unfortunately research is not an exact science: what looks good in a back-test environment may not pass muster when implemented in live trading. So researchers need to “iterate around” the idea, trying different combinations of entry and exit logic, for example, until they find a variant that works. Developers are lousy at this; GP systems excel at it.

CHALLENGES FOR THE GENETIC PROGRAMMING APPROACH

So enticing are the potential benefits of GP that it begs the question as to why the approach hasn’t been adopted more widely. One reason is the strong preference amongst researchers for an understandable – and testable – investment thesis. Researchers – and, more importantly, investors – are much more comfortable if they can articulate the premise behind a strategy. Even if a trade turns out to be a loser, we are generally more comfortable buying a stock on the supposition of, say, a positive outcome of a pending drug trial, than we are if required to trust the judgment of a black box, whose criteria are inherently unobservable.

Added to this, the GP approach suffers from three key drawbacks: data sufficiency, data mining and over-fitting. These are so well known that they hardly require further rehearsal. There have been many adverse outcomes resulting from poorly designed mechanical systems curve fitted to the data. Anyone who was active in the space in the 1990s will recall the hype over neural networks and the over-exaggerated claims made for their efficacy in trading system design. Genetic Programming, a far more general and powerful concept, suffered unfairly from the ensuing adverse publicity, although it does face many of the same challenges.

A NEW APPROACH

I began working in the field of genetic programming in the 1990’s, with my former colleague Haftan Eckholdt, at that time head of neuroscience at Yeshiva University, and we founded a hedge fund, Proteom Capital, based on that approach (large due to Haftan’s research). I and my colleagues at Systematic Strategies have continued to work on GP related ideas over the last twenty years, and during that period we have developed a methodology that address the weaknesses that have held back genetic programming from widespread adoption.

Firstly, we have evolved methods for transforming original data series that enables us to avoid over-using the same old data-sets and, more importantly, allows new patterns to be revealed in the underlying market structure. This effectively eliminates the data mining bias that has plagued the GP approach. At the same time, because our process produces a stronger signal relative to the background noise, we consume far less data – typically no more than a couple of years worth.

Secondly, we have found we can enhance the robustness of prototype strategies by using double-blind testing: i.e. data sets on which the performance of the model remains unknown to the machine, or the researcher, prior to the final model selection.

Finally, we are able to test not only the alpha signal, but also multiple variations of the trade expression, including different types of entry and exit logic, as well as profit targets and stop loss constraints.

OUTCOMES: ROBUST, PROFITABLE STRATEGIES

Taken together, these measures enable our GP system to produce strategies that not only have very high performance characteristics, but are also extremely robust. So, for example, having constructed a model using data only from the continuing bull market in equities in 2012 and 2013, the system is nonetheless capable of producing strategies that perform extremely well when tested out of sample over the highly volatility bear market conditions of 2008/09.

So stable are the results produced by many of the strategies, and so well risk-controlled, that it is possible to deploy leveraged money-managed techniques, such as Vince’s fixed fractional approach. Money management schemes take advantage of the high level of consistency in performance to increase the capital allocation to the strategy in a way that boosts returns without incurring a high risk of catastrophic loss. You can judge the benefits of applying these kinds of techniques in some of the strategies we have developed in equity, fixed income, commodity and energy futures which are described below.

CONCLUSION

After 20-30 years of incubation, the Genetic Programming approach to strategy research and development has come of age. It is now entirely feasible to develop trading systems that far outperform the overwhelming majority of strategies produced by human researchers, in a fraction of the time and for a fraction of the cost.

SAMPLE GP SYSTEMS