Category: Pairs Trading

Posted on

Applications of Graph Theory In Finance

Analyzing Big Data

Very large datasets – comprising voluminous numbers of symbols – present challenges for the analyst, not least of which is the difficulty of visualizing relationships between the individual component assets.  Absent the visual clues that are often highlighted by graphical images, it is easy for the analyst to overlook important changes in relationships.   One means of tackling the problem is with the use of graph theory.

SSALGOTRADING AD

DOW 30 Index Member Stocks Correlation Graph

In this example I have selected a universe of the Dow 30 stocks, together with a sample of commodities and bonds and compiled a database of daily returns over the period from Jan 2012 to Dec 2013.  If we want to look at how the assets are correlated, one way is to created an adjacency graph that maps the interrelations between assets that are correlated at some specified level (0.5 of higher, in this illustration).

g1

Obviously the choice of correlation threshold is somewhat arbitrary, and it is easy to evaluate the results dynamically, across a wide range of different threshold parameters, say in the range from 0.3 to 0.75:

animation

 

The choice of parameter (and time frame) may be dependent on the purpose of the analysis:  to construct a portfolio we might select a lower threshold value;  but if the purpose is to identify pairs for possible statistical arbitrage strategies, one will typically be looking for much higher levels of correlation.

Correlated Cliques

Reverting to the original graph, there is a core group of highly inter-correlated stocks that we can easily identify more clearly using the Mathematica function FindClique to specify graph nodes that have multiple connections:

g2

 

We might, for example, explore the relative performance of members of this sub-group over time and perhaps investigate the question as to whether relative out-performance or under-performance is likely to persist, or, given the correlation characteristics of this group, reverse over time to give a mean-reversion effect.


 g3

Constructing a Replicating Portfolio

An obvious application might be to construct a replicating portfolio comprising this equally-weighted sub-group of stocks, and explore how well it tracks the Dow index over time (here I am using the DIA ETF as a proxy for the index, for the sake of convenience):

g4

 

The correlation between the Dow index (DIA ETF) and the portfolio remains strong (around 0.91) throughout the out-of-sample period from 2014-2016, although the performance of the portfolio is distinctly weaker than that of the index ETF after the early part of 2014:

g7

 

Constructing Robust Portfolios

Another application might be to construct robust portfolios of lower-correlated assets.  Here for example we use the graph to identify independent vertices that have very few correlated relationships (designated using the star symbol in the graph below).  We can then create an equally weighted portfolio comprising the assets with the lowest correlations and compare its performance against that of the Dow Index.

The new portfolio underperforms the index during 2014, but with lower volatility and average drawdown.

g10

 

Conclusion – Graph Theory has Applications in Portfolio Constructions and Index Replication

Graph theory clearly has a great many potential applications in finance. It is especially useful as a means of providing a graphical summary of data sets involving a large number of complex interrelationships, which is at the heart of portfolio theory and index replication.  Another useful application would be to identify and evaluate correlation and cointegration relationships between pairs or small portfolios of stocks, as they evolve over time, in the context of statistical arbitrage.

 

 

 

 

Posted on

Pairs Trading – Part 2: Practical Considerations

Pairs Trading = Numbers Game

One of the first things you quickly come to understand in equity pairs trading is how important it is to spread your risk.  The reason is obvious: stocks are subject to a multitude of risk factors – amongst them earning shocks and corporate actions -that can blow up an otherwise profitable pairs trade.  Instead of the pair re-converging, they continue to diverge until you are stopped out of the position.  There is not much you can do about this, because equities are inherently risky.  Some arbitrageurs prefer trading ETF pairs for precisely this reason.  But risk and reward are two sides of the same coin:  risks tend to be lower in ETF pairs trades, but so, too, are the rewards.  Another factor to consider is that there are many more opportunities to be found amongst the vast number of stock combinations than in the much smaller universe of ETFs.  So equities remain the preferred asset class of choice for the great majority of arbitrageurs.

So, because of the risk in trading equities, it is vitally important to spread the risk amongst a large number of pairs.  That way, when one of your pairs trades inevitably blows up for one reason or another, the capital allocation is low enough not to cause irreparable damage to the overall portfolio.  Nor are you over-reliant on one or two star performers that may cease to contribute if, for example, one of the stock pairs is subject to a merger or takeover.

Does that mean that pairs trading is accessible only to managers with deep enough pockets to allocate broadly in the investment universe?  Yes and no.  On the one hand, of course, you need sufficient capital to allocate a meaningful sum to each of your pairs.  But pairs trading is highly efficient in its use of capital:  margin requirements are greatly reduced by the much lower risk of a dollar-neutral portfolio.  So your capital goes further than in would in a long-only strategy, for example.

How many pair combinations would you need to research to build an investment portfolio of the required size?  The answer might shock you:  millions.  Or  even tens of millions.  In the case of the Gemini Pairs strategy, for example, the universe comprises around 10m stock pairs and 200,000 ETF combinations.

It turns out to be much more challenging to find reliable stock pairs to trade than one might imagine, for reasons I am about to discuss.  So what tends to discourage investors from exploring pairs trading as an investment strategy is not because the strategy is inherently hard to understand; nor because the methods are unknown; nor because it requires vast amounts of investment capital to be viable.  It is that the research effort required to build a successful statistical arbitrage strategy is beyond the capability of the great majority of investors.

Before you become too discouraged, I will just say that there are at least two solutions to this challenge I can offer, which I will discuss later.

Methodology Isn’t a Decider

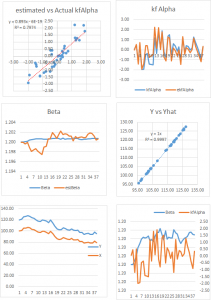
I have traded pairs successfully using all of the techniques described in the first part of the post (i.e. Ratio, Regression, Kalman and Copula methods).  Equally, I have seen a great many failed pairs strategies produced by using every available technique.  There is no silver bullet.  One often finds that a pair that perform poorly using the ratio method produces decent returns when a regression or Kalman Filter model is applied.  From experience, there is no pattern that allows you to discern which technique, if any, is gong to work.  You have to be prepared to try all of them, at least in back-test.

Correlation is Not the Answer

In a typical description of pairs trading the first order of business is often to look for a highly correlated pairs to trade.  While this makes sense as a starting point, it can never provide a complete answer.  The reason is well known:  correlations are unstable, and can often arise from random chance rather than as a result of a real connection between two stock processes.  The concept of spurious correlation is most easily grasped with an example, for instance:

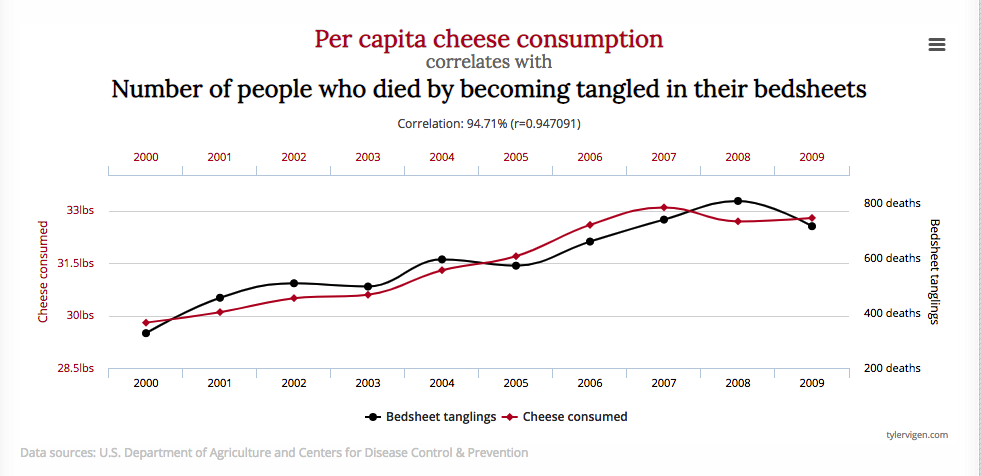
Of course, no rational person believes that there is a causal connection between cheese consumption and death by bedsheet entanglement – it is a spurious correlation that has arisen due to the random fluctuations in the two time series.  And because the correlation is spurious, the apparent relationship is likely to break down in future.

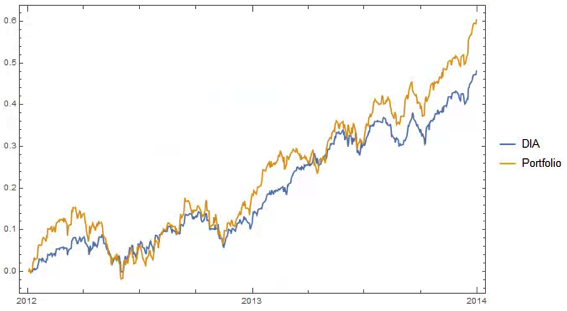
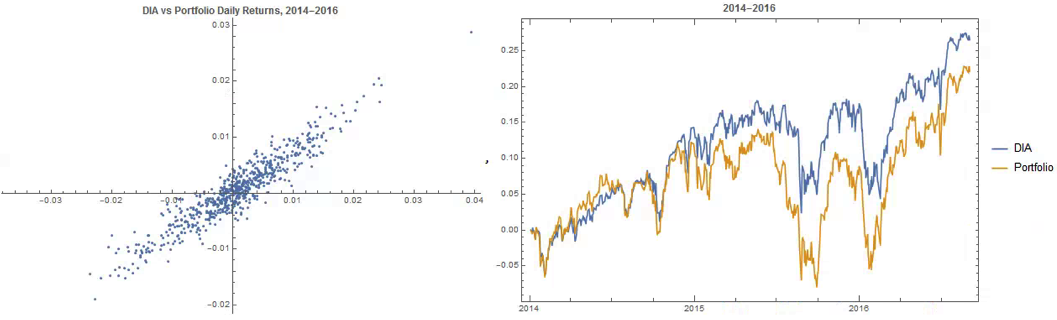
We can provide a slightly more realistic illustration as follows.  Let us suppose we have two correlated stocks, one with annual drift (i.e trend of 5% and annual volatility of 25%, the other with annual drift of 20% and annual volatility of 50%.  We assume that returns from the two processes follow a Normal distribution, with true correlation of 0.3.  Let’s assume that we sample the  returns for the two stocks over 90 days to estimate the correlation, simulating the real-world situation in which the true correlation is unknown.  Unlike in the real-world scenario, we can sample the 90-day returns many times (100,000 in this experiment) and look at the range of correlation estimates we observe:

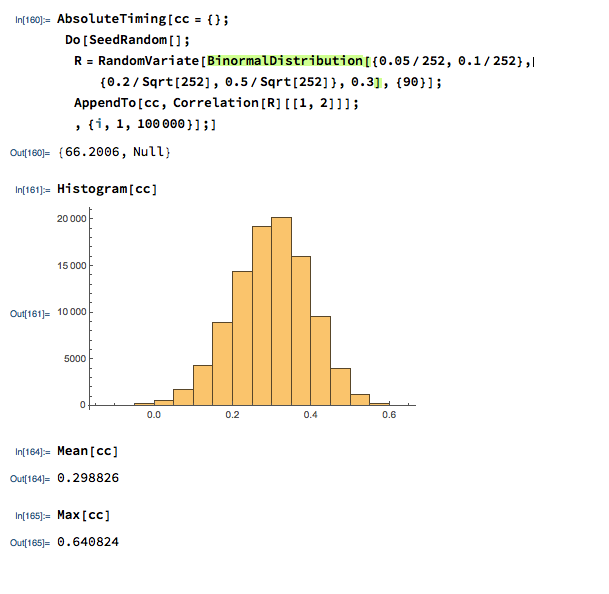
We find that, over the 100,000 repeated experiments the average correlation estimate is very close indeed to the true correlation.  However, in the real-world situation we only have a single observation, based on the returns from the two stock processes over the prior 90 days.  If we are very lucky, we might happen to pick a period in which the processes correlate at a level close to the true value of 0.3.  But as the experiment shows, we might be unlucky enough to see an estimate as high as 0.64, or as low as zero!

So when we look at historical data and use estimates of the correlation coefficient to gauge the strength of the relationship between two stocks, we are at the mercy of random variation in the sampling process, one that could suggest a much stronger (or weaker) connection than is actually the case.

One is on firmer ground in selecting pairs of stocks in the same sector, for example oil or gold-mining stocks, because we are able to identify causal factors that should provide a basis for a reliable correlation, such as the price of oil or gold.  This is indeed one of the “screens” that statistical arbitrageurs often use to select pairs for analysis.  But there are many examples of stocks that “ought” to be correlated but which nonetheless break down and drift apart.  This can happen for many reasons:  changes in the capital structure of one of the companies; a major product launch;  regulatory action; or corporate actions such as mergers and takeovers.

The bottom line is that correlation, while important, is not by itself a sufficiently reliable measure to provide a basis for pair selection.

Cointegration: the Drunk and His Dog

Suppose you see two drunks (i.e., two random walks) wandering around. The drunks don’t know each other (they’re independent), so there’s no meaningful relationship between their paths.

But suppose instead you have a drunk walking with his dog. This time there is a connection. What’s the nature of this connection? Notice that although each path individually is still an unpredictable random walk, given the location of one of the drunk or dog, we have a pretty good idea of where the other is; that is, the distance between the two is fairly predictable. (For example, if the dog wanders too far away from his owner, he’ll tend to move in his direction to avoid losing him, so the two stay close together despite a tendency to wander around on their own.) We describe this relationship by saying that the drunk and her dog form a cointegrating pair.

In more technical terms, if we have two non-stationary time series X and Y that become stationary when differenced (these are called integrated of order one series, or I(1) series; random walks are one example) such that some linear combination of X and Y is stationary (aka, I(0)), then we say that X and Y are cointegrated. In other words, while neither X nor Y alone hovers around a constant value, some combination of them does, so we can think of cointegration as describing a particular kind of long-run equilibrium relationship. (The definition of cointegration can be extended to multiple time series, with higher orders of integration.)

Other examples of cointegrated pairs:

  • Income and consumption: as income increases/decreases, so too does consumption.
  • Size of police force and amount of criminal activity
  • A book and its movie adaptation: while the book and the movie may differ in small details, the overall plot will remain the same.
  • Number of patients entering or leaving a hospital

So why do we care about cointegration? Someone else can probably give more econometric applications, but in quantitative finance, cointegration forms the basis of the pairs trading strategy: suppose we have two cointegrated stocks X and Y, with the particular (for concreteness) cointegrating relationship X – 2Y = Z, where Z is a stationary series of zero mean. For example, X could be McDonald’s, Y could be Burger King, and the cointegration relationship would mean that X tends to be priced twice as high as Y, so that when X is more than twice the price of Y, we expect X to move down or Y to move up in the near future (and analogously, if X is less than twice the price of Y, we expect X to move up or Y to move down). This suggests the following trading strategy: if X – 2Y > d, for some positive threshold d, then we should sell X and buy Y (since we expect X to decrease in price and Y to increase), and similarly, if X – 2Y < -d, then we should buy X and sell Y.

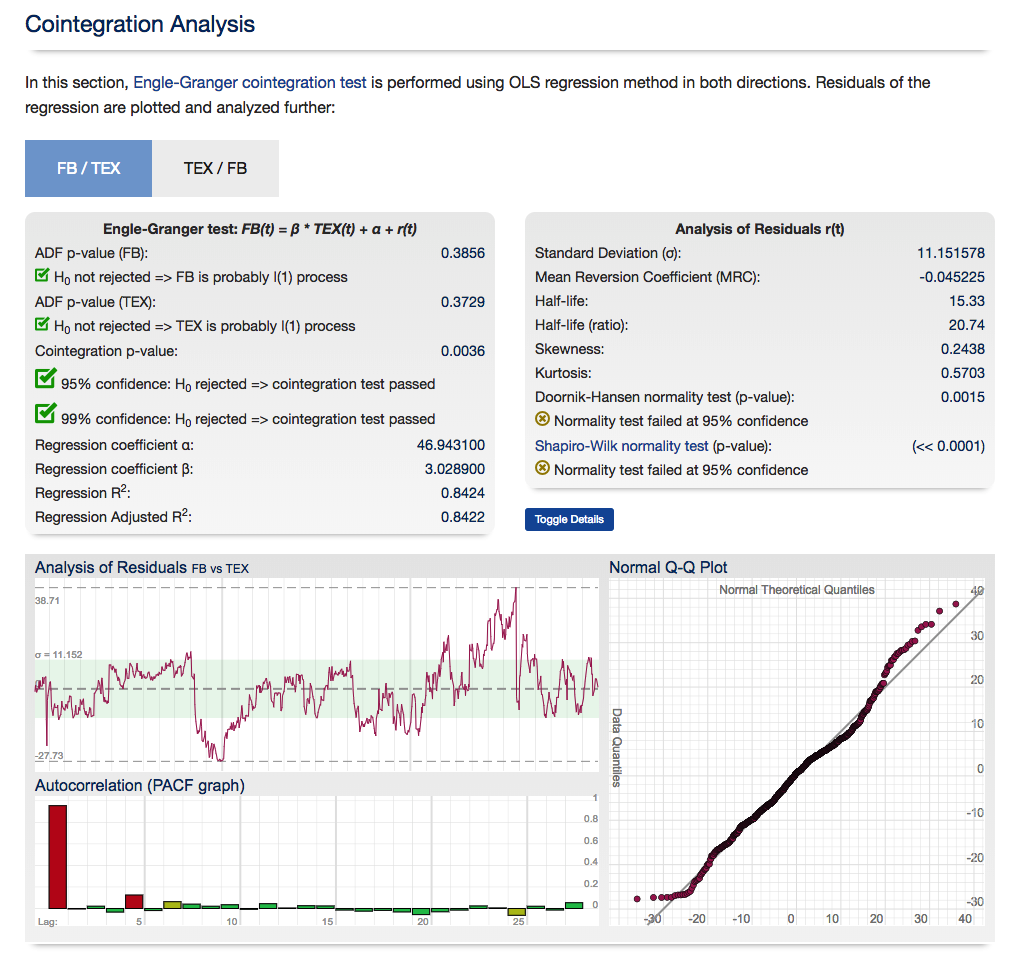
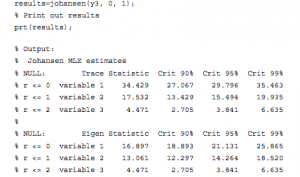
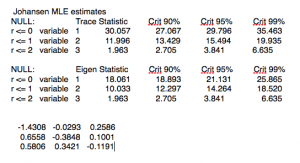
So how do you detect cointegration? There are several different methods, but the simplest is probably the Engle-Granger test, which works roughly as follows:

  • Check that Xt and Yt are both I(1).
  • Estimate the cointegrating relationship =+Yt=aXt+et by ordinary least squares.
  • Check that the cointegrating residuals et are stationary (say, by using a so-called unit root test, e.g., the Dickey-Fuller test).

Also, something else that should perhaps be mentioned is the relationship between cointegration and error-correction mechanisms: suppose we have two cointegrated series ,Xt,Yt, with autoregressive representations

=−1+−1+Xt=aXt−1+bYt−1+ut
=−1+−1+Yt=cXt−1+dYt−1+vt

By the Granger representation theorem (which is actually a bit more general than this), we then have

Δ=1(−1−−1)+ΔXt=α1(Yt−1−βXt−1)+ut
Δ=2(−1−−1)+ΔYt=α2(Yt−1−βXt−1)+vt

where −1−−1∼(0)Yt−1−βXt−1∼I(0) is the cointegrating relationship. Regarding −1−−1Yt−1−βXt−1 as the extent of disequilibrium from the long-run relationship, and the αi as the speed (and direction) at which the time series correct themselves from this disequilibrium, we can see that this formalizes the way cointegrated variables adjust to match their long-run equilibrium.

So, just to summarize a bit, cointegration is an equilibrium relationship between time series that individually aren’t in equilibrium (you can kind of contrast this with (Pearson) correlation, which describes a linear relationship), and it’s useful because it allows us to incorporate both short-term dynamics (deviations from equilibrium) and long-run expectations , i.e. corrections to equilibrium.  (My thanks to Edwin Chen for this entertaining explanation)

Cointegration is Not the Answer

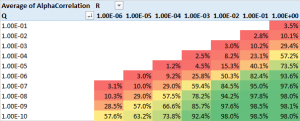
So a typical workflow for researching possible pairs trade might be to examine a large number of pairs in a sector of interest, select those that meet some correlation threshold (e.e. 90%), test those pairs for cointegration and select those that appear to be cointegrated.  The problem is:  it doesn’t work!  The pairs thrown up by this process are likely to work for a while, but many (even the majority) will break down at some point, typically soon after you begin live trading.  `The reason is that all of the major statistical tests for cointegration have relatively low power and pairs that are apparently cointegrated break down suddenly, with consequential losses for the trader.  The following posts delves into the subject in some detail:

 

Other Practical “Gotchas”

Apart from correlations/cointegration breakdowns there is a long list of things that can go wrong with a pairs trade that the practitioner needs to take account of, for instance:

  • A stock may become difficult or expensive to short
  • The overall backtest performance stats for a pair may look great, but the P&L per share is too small to overcome trading costs and other frictions.
  • Corporate actions (mergers, takeovers) and earnings can blow up one side of an otherwise profitable pair.
  • It is possible to trade passively, crossing the spread  to trade the other leg when the first leg trades.  But this trade expression is challenging to test.  If paying the spread on both legs is going to jeopardize the profitability of the strategy, it is probably better to reject the pair.

What Works

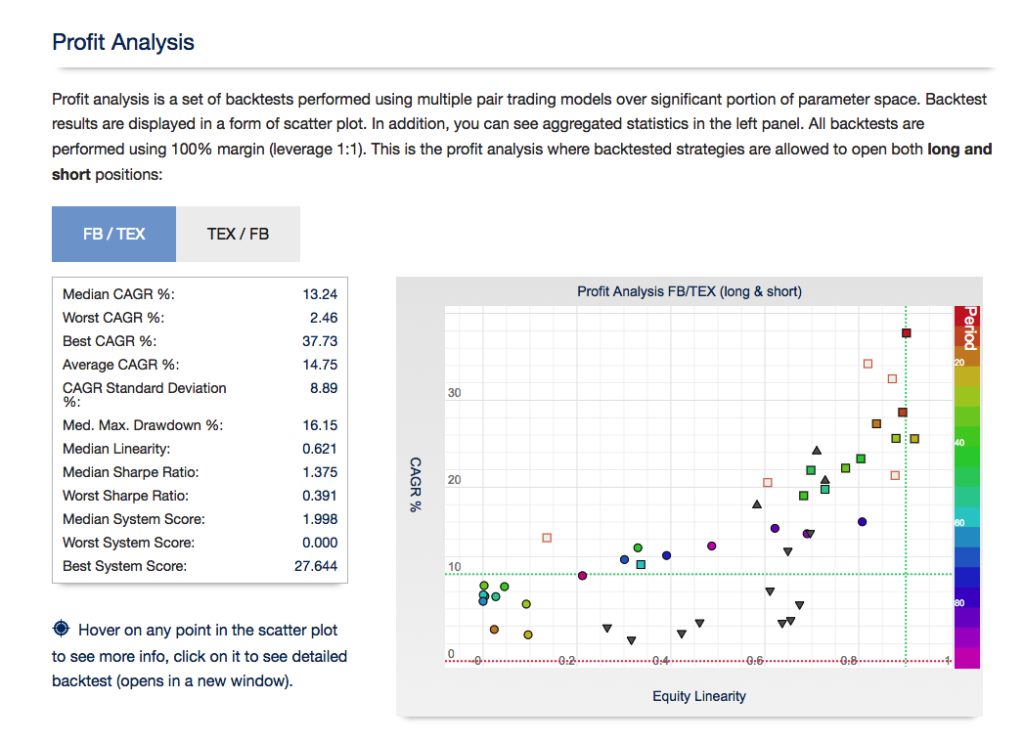
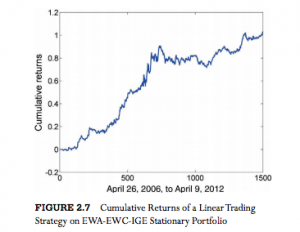
From my experience, the testing phase of the process of building a statistical arbitrage strategy is absolutely critical.  By this I mean that, after screening for correlation and cointegration, and back-testing all of the possible types of model, it is essential to conduct an extensive simulation test over a period of several weeks before adding a new pair to the production system.  Testing is important for any algorithmic strategy, of course, but it is an integral part of the selection process where pairs trading is concerned.  You should expect 60% to 80% of your candidates to fail in simulated trading, even after they have been carefully selected and thoroughly back-tested.  The good good news is that those pairs that pass the final stage of testing usually are successful in a production setting.

Implementation

Putting all of this information together, it should be apparent that the major challenge in pairs trading lies not so much in understanding and implementing methodologies and techniques, but in implementing the research process on an industrial scale, sufficient to collate and analyze tens of millions of pairs. This is beyond the reach of most retail investors, and indeed, many small trading firms:  I once worked with a trading firm for over a year on a similar research project, but in the end it proved to be capabilities of even their highly competent development team.

So does this mean that for the average quantitative strategist investors statistical arbitrage must remain an investment concept of purely theoretical interest?  Actually, no.  Firstly, for the investor, there are plenty of investment products available that they can access via hedge fund structures (or even our algotrading platform, as I have previously mentioned).

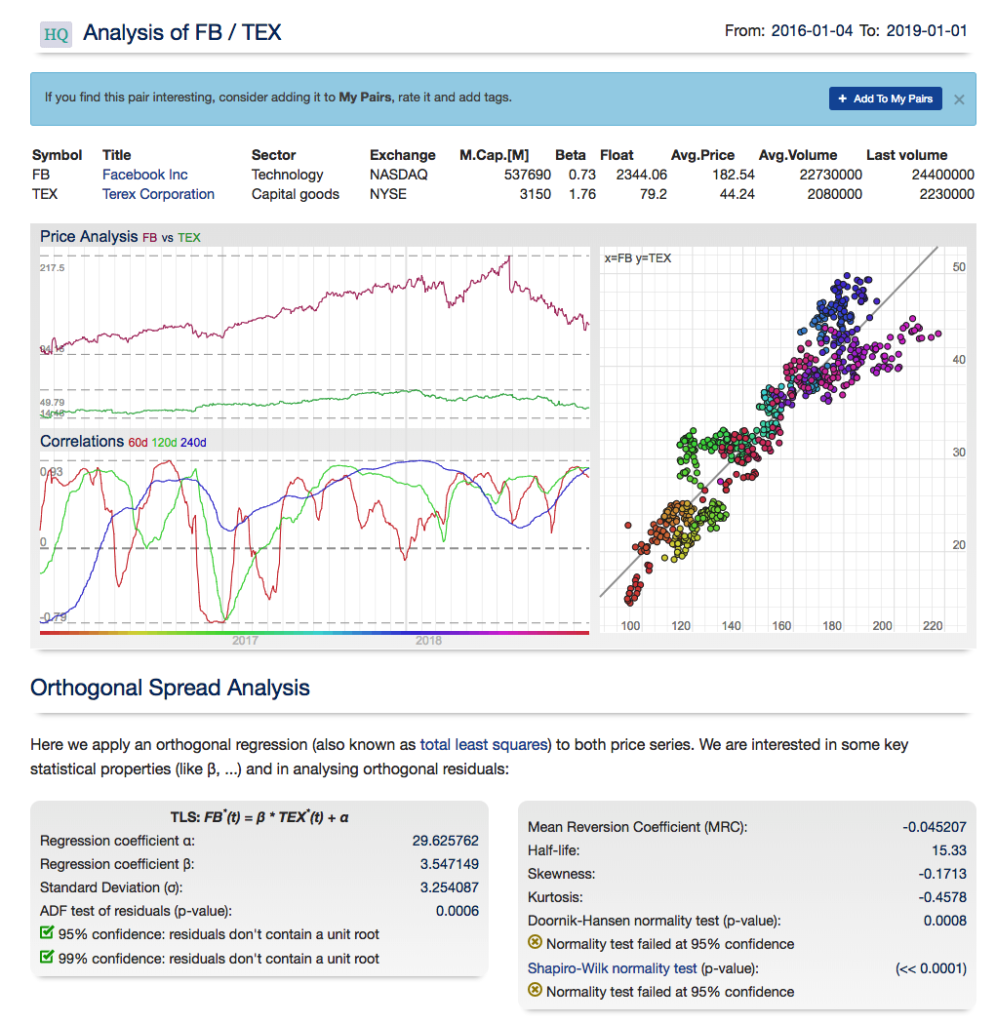
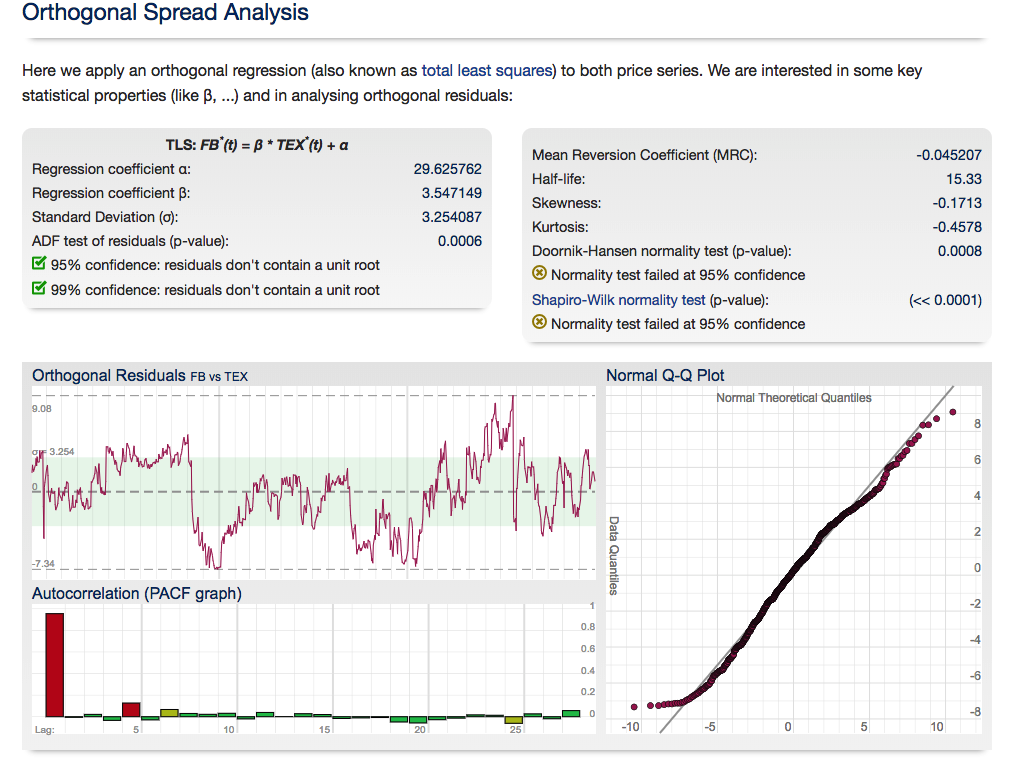
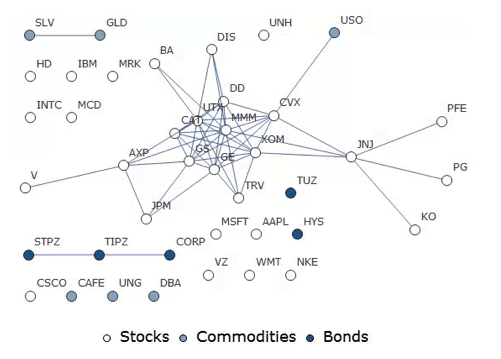
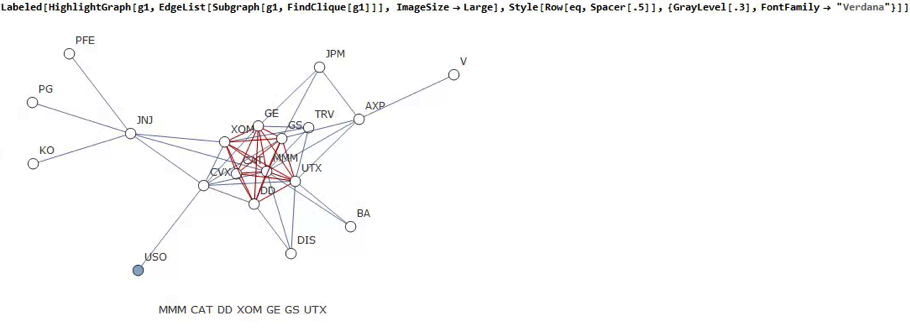
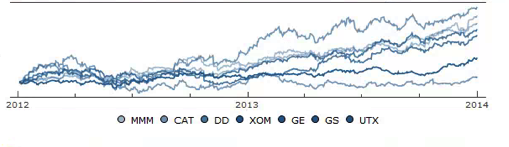
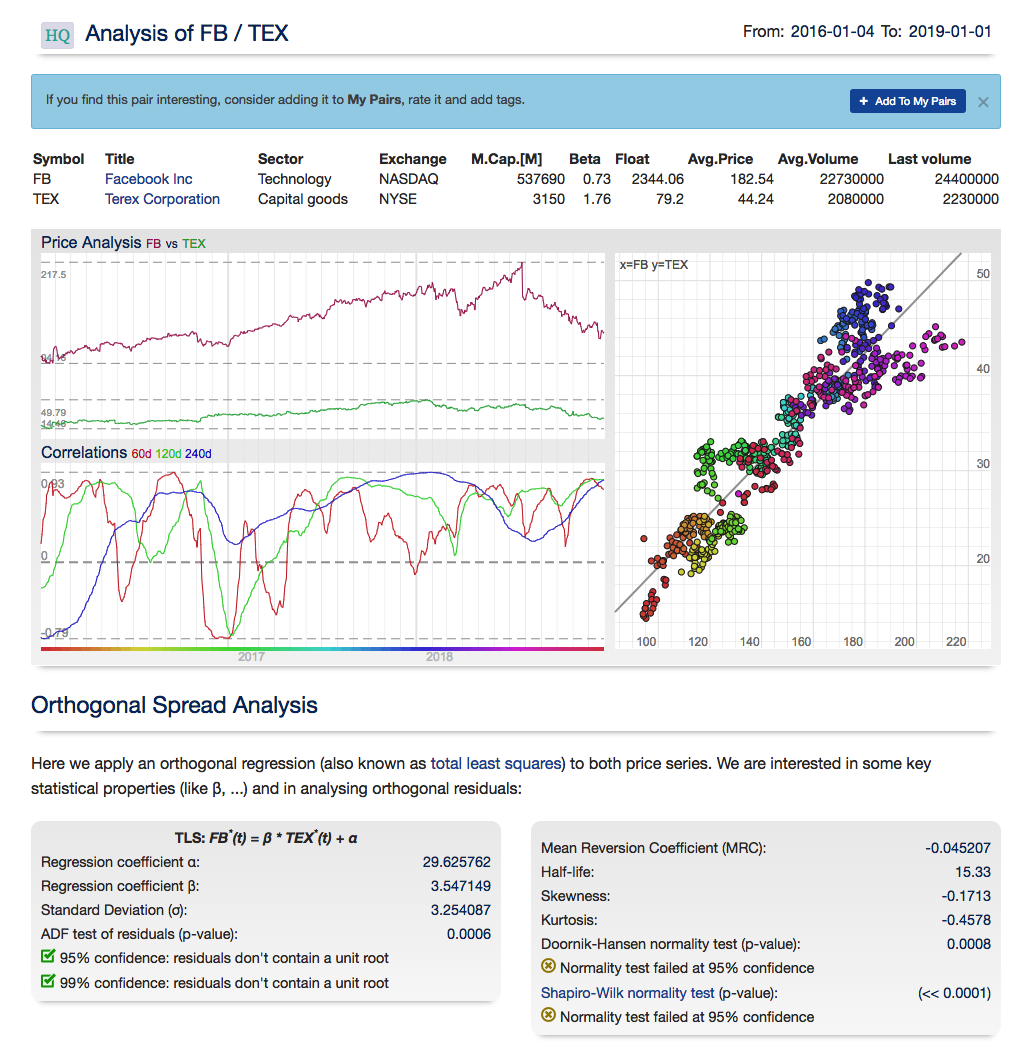
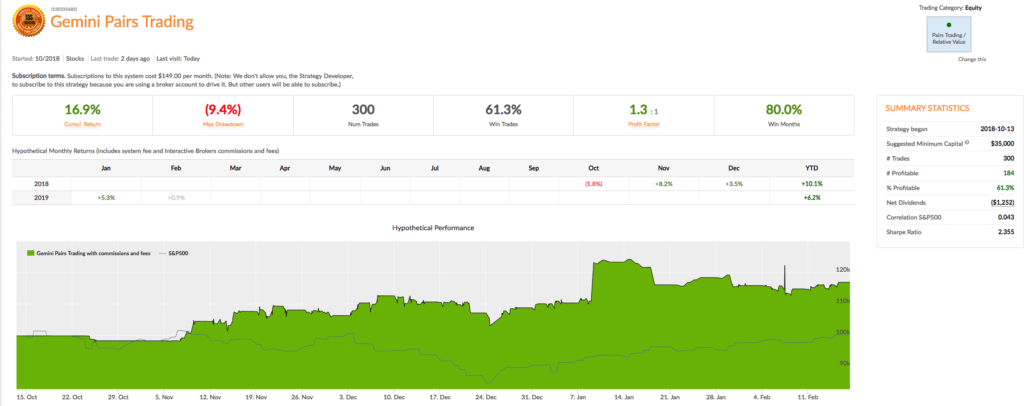
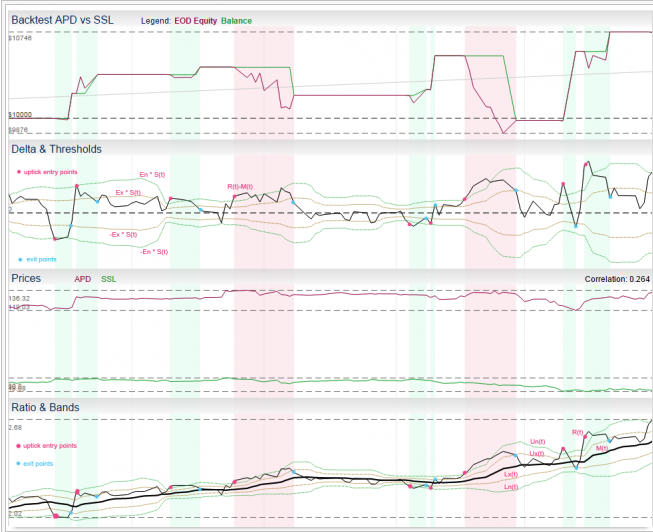
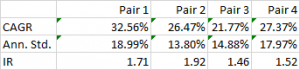
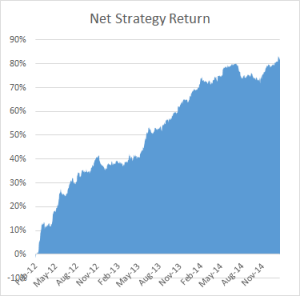
For those interested in building stat arb strategies there is an excellent resource that collates all of the data and analysis on tens of millions of stock pairs that enables the researcher to identify promising pairs, test their level of cointegration, backtest strategies using different methodologies and even put selected pars strategies into production (see example below).

Those interested should contact me for more information.

 

Posted on

Pairs Trading in Practice

Part 1 – Methodologies

It is perhaps a little premature for a deep dive into the Gemini Pairs Trading strategy which trades on our Systematic Algotrading platform.  At this stage all one can say for sure is that the strategy has made a pretty decent start – up around 17% from October 2018.  The strategy does trade multiple times intraday, so the record in terms of completed trades – numbering over 580 – is appreciable (the web site gives a complete list of live trades).  And despite the turmoil through the end of last year the Sharpe Ratio has ranged consistently around 2.5.

One of the theoretical advantages of pairs trading is, of course, that the coupling of long and short positions in a relative value trade is supposed to provide a hedge against market downdrafts, such as we saw in Q4 2018.  In that sense pairs trading is the quintessential hedge fund strategy, embodying the central concept on which the entire edifice of hedge fund strategies is premised.
In practice, however, things often don’t work out as they should. In this thread I want to spend a little time reviewing why that is and to offer some thoughts based on my own experience of working with statistical arbitrage strategies over many years.

Methodology

There is no “secret recipe” for pairs trading:  the standard methodologies are as well known as the strategy concept.  But there are some important practical considerations that I would like to delve into in this post.  Before doing that, let me quickly review the tried and tested approaches used by statistical arbitrageurs.

The Ratio Model is one of the standard pair trading models described in literature. It is based in ratio of instrument prices, moving average and standard deviation. In other words, it is based on Bollinger Bands indicator.

  • we trade pair of stocks A, B, having price series A(t), B(t)
  • we need to calculate ratio time series R(t) = A(t) / B(t)
  • we apply a moving average of type T with period Pm on R(t) to get time series M(t)
  • Next we apply the standard deviation with period Ps on R(t) to get time series S(t)
  • now we can create Z-score series Z(t) as Z(t) = (R(t) – M(t)) / S(t), this time series can give us z-score to signal trading decision directly (in reality we have two Z-scores: Z-scoreask and Z-scorebid as they are calculated using different prices, but for the sake of simplicity let’s now pretend we don’t pay bid-ask spread and we have just one Z-score)

Another common way to visualize  this approach is to think in terms of bands around the moving average M(t):

  • upper entry band Un(t) = M(t) + S(t) * En
  • lower entry band Ln(t) = M(t) – S(t) * En
  • upper exit band Ux(t) = M(t) + S(t) * Ex
  • lower exit band Lx(t) = M(t) – S(t) * Ex

These bands are actually the same bands as in Bollinger Bands indicator and we can use crossing of R(t) and bands as trade signals.

  • We open short pair position, if the Z-score Z(t) >= En (equivalent to R(t) >= Un(t))
  • We open long pair position if the Z-score Z(t) <= -En (equivalent to R(t) <= Ln(t))

In the Regression, Residual or Cointegration approach we construct a linear regression between A(t), B(t) using OLS, where A(t) = β * B(t) + α + R(t)

Because we use a moving window of period P (we calculate new regression each day), we actually get new series β(t), α(t), R(t), where β(t), α(t) are series of regression coefficients and R(t) are residuals (prediction errors)

  • We look at the residuals series  R(t) = A(t) – (β(t) * B(t) + α(t))
  • We next calculate the standard deviation of the residuals R(t), which we designate S(t)
  • Now we can create Z-score series Z(t) as Z(t) = R(t) / S(t) – the time series that is used to generate trade signals, just as in the Ratio model.

The Kalman Filter model provides superior estimates of the current hedge ratio compared to the Regression method.  For a detailed explanation of the techniques, see the following posts (the post on ETF trading contains complete Matlab code).

 

 

Finally,  the rather complex Copula methodology models the joint and margin distributions of the returns process in each stock as described in the following post

Posted on

Successful Statistical Arbitrage

 

I tend not to get involved in Q&A with readers of my blog, or with investors.  I am at a point in my life where I spend my time mostly doing what I want to do, rather than what other people would like me to do.  And since I enjoy doing research and trading, I try to maximize the amount of time I spend on those activities.

As a business strategy, I wouldn’t necessarily recommend this approach.  It’s just something I evolved while learning to play chess: since I had no-one to teach me, I had to learn everything for myself and this involved studying for many, many hours alone.

By contrast, several of the best money managers are also excellent communicators – take Roy Niederhoffer, or Ernie Chan, for example. Having regular, informed communication with your investors is, as smarter managers have realized, a means of building trust and investor loyalty – important factors that come into play during periods when your strategy is underperforming. Not only that, but since communication is two-way, an analyst/manager can learn much from his exchanges with his clients.  Knowing how others perceive you – and your competitors – for example, is very useful information.  So, too, is information about your competitors’ research ideas, investment strategies and fund performance, which can often be gleaned from discussions with investors.  There are plenty of reasons to prefer a policy of regular, open communication.

As a case in point, I was surprised to learn from  comments on another research blog that readers drew the conclusion from my previous posts that pursuing the cointegration or Kalman Filter approach to statistical arbitrage was a waste of time.  Apparently, my remark to the effect that researchers often failed to pay attention to the net PnL per share in evaluating stat. arb. trading strategies was taken by some to mean that any apparent profitability would always be subsumed within the bid-offer spread.  That was not my intention.  What I intended to convey was that in some instances, this would be the case  – some, but not all.

To illustrate the point, below are the out-of-sample results from a research study applying the Kalman Filter approach for four equity pairs using 5-minute data.  For competitive reasons I am unable to identify the specific stocks in each pair, which result from an exhaustive analysis of over 30,000 pairs, but I can say that they are liquid large-cap equities traded in large volume on the US exchanges.  The performance numbers are net of transaction costs and are based on the assumption of a 5-minute delay in execution: meaning, a trading signal received at time t is assumed to be executed at time t+5 minutes.  This allows sufficient time to leg into each trade passively, in most cases avoiding the bid-offer spread.  The net PnL per share is above 1.5c per share for each pair.

Fig 0 While the performance of none of the pairs is spectacular, a combined portfolio has quite attractive characteristics, which include 81% winning months since Jan 2012, a CAGR of over 27% and Information Ratio of 2.29, measured on monthly returns (2.74 based on daily returns).

Fig 2

Fig 3

Finally, I am currently implementing trading of a number of stock portfolios based on static cointegration relationships that have out-of-sample information ratios of between 3 and 4, using daily data.

 

 

Posted on

Statistical Arbitrage Using the Kalman Filter

One of the challenges with the cointegration approach to statistical arbitrage which I discussed in my previous post, is that cointegration relationships are seldom static: they change quite frequently and often break down completely.  Back in 2009 I began experimenting with a more dynamic approach to pairs trading, based on the Kalman Filter.

 

In its simplest form, we  model the relationship between a pair of securities in the following way:

beta(t) = beta(t-1) + w     beta(t), the unobserved state variable, that follows a random walk

Y(t) = beta(t)X(t) + v      The observed processes of stock prices Y(t) and X(t)

where:

w ~ N(0,Q) meaning w is gaussian noise with zero mean and variance Q

v ~ N(0,R) meaning v is gaussian noise with variance R

So this is just like the usual pairs relationship Y = beta * X + v, where the typical approach is to estimate beta using least squares regression, or some kind of rolling regression (to try to take account of the fact that beta may change over time).  In this traditional framework, beta is static, or slowly changing.

In the Kalman framework, beta is itself a random process that evolves continuously over time, as a random walk.  Because it is random and contaminated by noise we cannot observe beta directly, but must infer its (changing) value from the observable stock prices X and Y. (Note: in what follows I shall use X and Y to refer to stock prices.  But you could also use log prices, or returns).

Unknown to me at that time,  several other researchers were thinking along the same lines and later published their research.  One such example is Statistical Arbitrage and High-Frequency Data with an Application to Eurostoxx 50 Equities,  Rudy, Dunis, Giorgioni and Laws, 2010.  Another closely related study is  Performance Analysis of Pairs Trading Strategy Utilizing High Frequency Data with an Application to KOSPI 100 Equities, Kim, 2011.  Both research studies follow a very similar path, rejecting beta estimation using rolling regression or exponential smoothing in favor of the Kalman approach and applying a Ornstein-Uhlenbeck model to estimate the half-life of mean reversion of the pairs portfolios.  The studies report very high out-of-sample information ratios that in some cases exceed 3.

I have already made the point that such unusually high performance is typically the result of ignoring the fact that the net PnL per share may lie within the region of the average bid-offer spread, making implementation highly problematic.  In this post I want to dwell on another critical issue that is particular to the Kalman approach: the signal:noise ratio, Q/R, which expresses the ratio of the variance of the beta process to that of the price process.  (Curiously, both papers make the same mistake of labelling Q and R as standard deviations. In fact, they are variances).

Beta, being a random process, obviously contains some noise:  but the hope is that it is less noisy than the price process.  The idea is that the relationship between two stocks is more stable – less volatile – than the stock processes themselves.  On its face, that assumption appears reasonable, from an empirical standpoint.  The question is:  how stable is the beta process, relative to the price process? If the variance in the beta process is  low relative to the price process,  we can determine beta quite accurately over time and so obtain accurate estimates of the true price Y(t), based on X(t).  Then, if we observe a big enough departure in the quoted price Y(t) from the true price at time t, we have a potential trade.

In other words, we are interested in:

alpha(t) = Y(t) – Y*(t) = Y(t) – beta(t) X(t)

where Y(t) and X(t) are the observed stock prices and beta(t) is the estimated value of beta at time t.

As usual, we would standardize the alpha using an estimate of the alpha standard deviation, which is sqrt(R).  (Alternatively, you can estimate the standard deviation of the alpha directly, using a lookback period based on the alpha half-life).

If the standardized alpha is large enough, the model suggests that the price Y(t) is quoted significantly in excess of the true value.  Hence we would short stock Y and buy stock X.  (In this context, where X and Y represent raw prices, you would hold an equal and opposite number of shares in Y and X.  If X and Y represented returns, you would hold equal and opposite market value in each stock).

The success of such a strategy depends critically on the quality of our estimates of alpha, which in turn rest on the accuracy of our estimates of beta. This depends on the noisiness of the beta process, i.e. its variance, Q.  If the beta process is very noisy, i.e. if Q is large, our estimates of alpha are going to be too noisy to be useful as the basis for a reversion strategy.

So, the key question I want to address in this post is: in order for the Kalman approach to be effective in modeling a pairs relationship, what would be an acceptable range for the beta process variance Q ?  (It is often said that what matters in the Kalman framework is not the variance Q, per se, but rather the signal:noise ratio Q/R.  It turns out that this is not strictly true, as we shall see).

To get a handle on the problem, I have taken the following approach:

(i) Simulate a stock process X(t) as a geometric brownian motion process with specified drift and volatility (I used 0%,  5% and 10% for the annual drift, and 10%,  30% and 60% for the corresponding annual volatility).

(ii) simulate a beta(t) process as a random walk with variance Q in the range from 1E-10 to 1E-1.

(iii) Generate the true price process Y(t) = beta(t)* X(t)

(iv) Simulate an observed price process Yobs(t), by adding random noise with variance R to Y(t), with R in the range 1E-6 to 1.0

(v) Calculate the true, known alpha(t) = Y(t) – Yobs(t)

(vi) Fit the Kalman Filter model to the simulated processes and estimate beta(t)  and Yest(t). Hence produce estimates kfalpha(t)  = Yobs(t) – Yest(t) and compare these with the known, true alpha(t).

The charts in Fig. 1 below illustrate the procedure for a stock process X(t) with annual drift of 10%, annual volatility 40%, beta process variance Q of 8.65E-9 and price process variance R of 5.62E-2 (Q/R ratio of 1.54E-7).

Fig 1

Fig. 1 True and Estimated Beta and Alpha Using the Kalman Filter

As you can see, the Kalman Filter does  a very good job of updating its beta estimate to track the underlying, true beta (which, in this experiment, is known). As the noise ratio Q/R is small, the Kalman Filter estimates of the process alpha, kfalpha(t), correspond closely to the true alpha(t), which again are known to us in this experimental setting.  You can examine the relationship between the true alpha(t) and the Kalman Filter estimates kfalpha(t) is the chart in the upmost left quadrant of the figure.  The correlation between the two is around 89%.  With a level of accuracy this good for our alpha estimates, the pair of simulated stocks would make an ideal candidate for a pairs trading strategy.

Of course, the outcome is highly dependent on the values we assume for Q and R (and also to some degree on the assumptions made about the drift and volatility of the price process X(t)).

The next stage of the analysis is therefore to generate a large number of simulated price and beta observations and examine the impact of different levels of Q and R, the variances of the beta and price process.  The results are summarized in the table in Fig 2 below.

Fig 2

 Fig 2. Correlation between true alpha(t) and kfalpha(t) for values of Q and R

As anticipated, the correlation between the true alpha(t) and the estimates produced by the Kalman Filter is very high when the signal:noise ratio is small, i.e. of the order of 1E-6, or less.  Average correlations begin to tail off very quickly when Q/R exceeds this level, falling to as low as 30% when the noise ratio exceeds 1E-3.  With a Q/R ratio of 1E-2 or higher, the alpha estimates become too noisy to be useful.

I find it rather fortuitous, even implausible, that in their study Rudy, et al, feel able to assume a noise ratio of 3E-7 for all of the stock pairs in their study, which just happens to be in the sweet spot for alpha estimation.  From my own research, a much larger value in the region of 1E-3 to 1E-5 is  more typical. Furthermore, the noise ratio varies significantly from pair to pair, and over time.  Indeed, I would go so far as to recommend applying a noise ratio filter to the strategy, meaning that trading signals are ignored when the noise ratio exceeds some specified level.

The take-away is this:  the Kalman Filter approach can be applied very successfully in developing statistical arbitrage strategies, but only for processes where the noise ratio is not too large.  One suggestion is to use a filter rule to supress trade signals generated at times when the noise ratio is too large, and/or to increase allocations to pairs in which the noise ratio is relatively low.

 

 

 

Posted on

Developing Statistical Arbitrage Strategies Using Cointegration

In his latest book (Algorithmic Trading: Winning Strategies and their Rationale, Wiley, 2013) Ernie Chan does an excellent job of setting out the procedures for developing statistical arbitrage strategies using cointegration.  In such mean-reverting strategies, long positions are taken in under-performing stocks and short positions in stocks that have recently outperformed.

I will leave a detailed description of the procedure to Ernie (see pp 47 – 60), which in essence involves:

(i) estimating a cointegrating relationship between two or more stocks, using the Johansen procedure

(ii) computing the half-life of mean reversion of the cointegrated process, based on an Ornstein-Uhlenbeck  representation, using this as a basis for deciding the amount of recent historical data to be used for estimation in (iii)

(iii) Taking a position proportionate to the Z-score of the market value of the cointegrated portfolio (subtracting the recent mean and dividing by the recent standard deviation, where “recent” is defined with reference to the half-life of mean reversion)

Countless researchers have followed this well worn track, many of them reporting excellent results.  In this post I would like to discuss a few of many considerations  in the procedure and variations in its implementation.  We will follow Ernie’s example, using daily data for the EWF-EWG-ITG triplet of ETFs from April 2006 – April 2012. The analysis runs as follows (I am using an adapted version of the Matlab code provided with Ernie’s book):

Johansen test We reject the null hypothesis of fewer then three cointegrating relationships at the 95% level. The eigenvalues and eigenvectors are as follows:

Eigenvalues The eignevectors are sorted by the size of their eigenvalues, so we pick the first of them, which is expected to have the shortest half-life of mean reversion, and create a portfolio based on the eigenvector weights (-1.046, 0.76, 0.2233).  From there, it requires a simple linear regression to estimate the half-life of mean reversion:

Halflife From which we estimate the half-life of mean reversion to be 23 days.  This estimate gets used during the final, stage 3, of the process, when we choose a look-back period for estimating the running mean and standard deviation of the cointegrated portfolio.  The position in each stock (numUnits) is sized according to the standardized deviation from the mean (i.e. the greater the deviation the larger the allocation). Apply Ci The results appear very promising, with an annual APR of 12.6% and Sharpe ratio of 1.4:   Returns EWA-EWC-IGE

Ernie is at pains to point out that, in this and other examples in the book, he pays no attention to transaction costs, nor to the out-of-sample performance of the strategies he evaluates, which is fair enough.

The great majority of the academic studies that examine the cointegration approach to statistical arbitrage for a variety of investment universes do take account of transaction costs.  For the most part such studies report very impressive returns and Sharpe ratios that frequently exceed 3.  Furthermore, unlike Ernie’s example which is entirely in-sample, these studies typically report consistent out-of-sample performance results also.

But the single, most common failing of such studies is that they fail to consider the per share performance of the strategy.  If the net P&L per share is less than the average bid-offer spread of the securities in the investment portfolio, the theoretical performance of the strategy is unlikely to survive the transition to implementation.  It is not at all hard to achieve a theoretical Sharpe ratio of 3 or higher, if you are prepared to ignore the fact that the net P&L per share is lower than the average bid-offer spread.  In practice, however, any such profits are likely to be whittled away to zero in trading frictions – the costs incurred in entering, adjusting and exiting positions across multiple symbols in the portfolio.

Put another way, you would want to see a P&L per share of at least 1c, after transaction costs, before contemplating implementation of the strategy.  In the case of the EWA-EWC-IGC portfolio the P&L per share is around 3.5 cents.  Even after allowing, say, commissions of 0.5 cents per share and a bid-offer spread of 1c per share on both entry and exit, there remains a profit of around 2 cents per share – more than enough to meet this threshold test.

Let’s address the second concern regarding out-of-sample testing.   We’ll introduce a parameter to allow us to select the number of in-sample days, re-estimate the model parameters using only the in-sample data, and test the performance out of sample.  With a in-sample size of 1,000 days, for instance, we find that we can no longer reject the null hypothesis of fewer than 3 cointegrating relationships and the weights for the best linear portfolio differ significantly from those estimated using the entire data set.

Johansen 2

Repeating the regression analysis using the eigenvector weights of the maximum eigenvalue vector (-1.4308, 0.6558, 0.5806), we now estimate the half-life to be only 14 days.  The out-of-sample APR of the strategy over the remaining 500 days drops to around 5.15%, with a considerably less impressive Sharpe ratio of only 1.09.

osPerfOut-of-sample cumulative returns

One way to improve the strategy performance is to relax the assumption of strict proportionality between the portfolio holdings and the standardized deviation in the market value of the cointegrated portfolio.  Instead, we now require  the standardized deviation of the portfolio market value to exceed some chosen threshold level before we open a position (and we close any open positions when the deviation falls below the threshold).  If we choose a threshold level of 1, (i.e. we require the market value of the portfolio to deviate 1 standard deviation from its mean before opening a position), the out-of-sample performance improves considerably:

osPerf 2

The out-of-sample APR is now over 7%, with a Sharpe ratio of 1.45.

The strict proportionality requirement, while logical,  is rather unusual:  in practice, it is much more common to apply a threshold, as I have done here.  This addresses the need to ensure an adequate P&L per share, which will typically increase with higher thresholds.  A countervailing concern, however, is that as the threshold is increased the number of trades will decline, making the results less reliable statistically.  Balancing the two considerations, a threshold of around 1-2 standard deviations is a popular and sensible choice.

Of course, introducing thresholds opens up a new set of possibilities:  just because you decide to enter based on a 2x SD trigger level doesn’t mean that you have to exit a position at the same level.  You might consider the outcome of entering at 2x SD, while exiting at 1x SD, 0x SD, or even -2x SD.  The possible nuances are endless.

Unfortunately, the inconsistency in the estimates of the cointegrating relationships over different data samples is very common.  In fact, from my own research, it is often the case that cointegrating relationships break down entirely out-of-sample, just as do correlations.  A recent study by Matthew Clegg of over 860,000 pairs confirms this finding (On the Persistence of Cointegration in Pais Trading, 2014) that cointegration is not a persistent property.

I shall examine one approach to  addressing the shortcomings  of the cointegration methodology  in a future post.

 

Matlab code (adapted from Ernie Chan’s book):

Continue reading “Developing Statistical Arbitrage Strategies Using Cointegration”