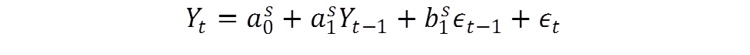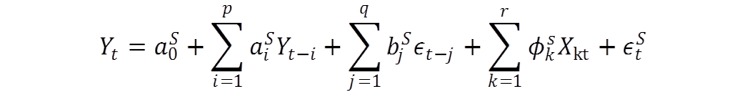The Excel workbook referred to in this post can be downloaded here.
Market state models are amongst the most useful analytical techniques that can be helpful in developing alpha-signal generators. That term covers a great deal of ground, with ideas drawn from statistics, econometrics, physics and bioinformatics. The purpose of this short note is to provide an introduction to some of the key ideas and suggest ways in which they might usefully applied in the context of researching and developing trading systems.
Although they come from different origins, the concepts presented here share common foundational principles:
- Markets operate in different states that may be characterized by various measures (volatility, correlation, microstructure, etc);
- Alpha signals can be generated more effectively by developing models that are adapted to take account of different market regimes;
- Alpha signals may be combined together effectively by taking account of the various states that a market may be in.
Market state models have shown great promise is a variety of applications within the field of applied econometrics in finance, not only for price and market direction forecasting, but also basis trading, index arbitrage, statistical arbitrage, portfolio construction, capital allocation and risk management.
REGIME SWITCHING MODELS
These are econometric models which seek to use statistical techniques to characterize market states in terms of different estimates of the parameters of some underlying linear model. This is accompanied by a transition matrix which estimates the probability of moving from one state to another.
To illustrate this approach I have constructed a simple example, given in the accompanying Excel workbook. In this model the market operates as follows:
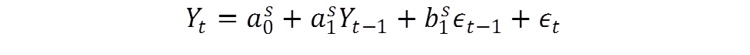 Where
Where
Yt is a variable of interest (e.g. the return in an asset over the next period t)
et is an error process with constant variance s2
S is the market state, with two regimes (S=1 or S=2)
a0 is the drift in the asset process
a1 is an autoregressive term, by which the return in the current period is dependent on the prior period return
b1 is a moving average term, which smoothes the error process
This is one of the simplest possible structures, which in more general form can include multiple states, and independent regressions Xi as explanatory variables (such as book pressure, order flow, etc):
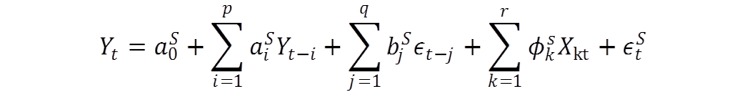

The form of the error process et may also be dependent on the market state. It may simply be that, as in this example, the standard deviation of the error process changes from state to state. But the changes can also be much more complex: for instance, the error process may be non-Gaussian, or it may follow a formulation from the GARCH framework.
In this example the state parameters are as follows:
|
Reg1 |
Reg 2 |
| s |
0.01 |
0.02 |
| a0 |
0.005 |
-0.015 |
| a1 |
0.40 |
0.70 |
| b1 |
0.10 |
0.20 |
What this means is that, in the first state the market tends to trend upwards with relatively low volatility. In the second state, not only is market volatility much higher, but also the trend is 3x as large in the negative direction.
I have specified the following state transition matrix:
|
Reg1 |
Reg2 |
| Reg1 |
0.85 |
0.15 |
| Reg2 |
0.90 |
0.10 |
This is interpreted as follows: if the market is in State 1, it will tend to remain in that state 85% of the time, transitioning to State 2 15% of the time. Once in State 2, the market tends to revert to State 1 very quickly, with 90% probability. So the system is in State 1 most of the time, trending slowly upwards with low volatility and occasionally flipping into an aggressively downward trending phase with much higher volatility.
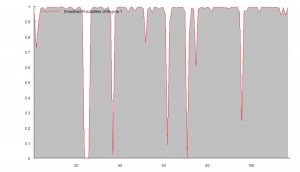
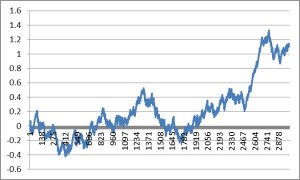
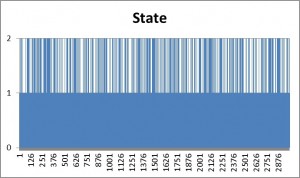
The Generate sheet in the Excel workbook shows how observations are generated from this process, from which we select a single instance of 3,000 observations, shown in sheet named Sample.
The sample looks like this:
As anticipated, the market is in State 1 most of the time, occasionally flipping into State 2 for brief periods.
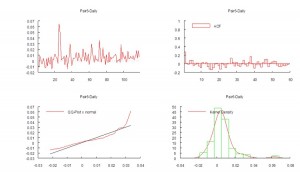
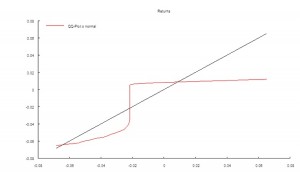
It is well-known that in financial markets we are typically dealing with highly non-Gaussian distributions. Non-Normality can arise for a number of reasons, including changes in regimes, as illustrated here. It is worth noting that, even though in this example the process in either market state follows a Gaussian distribution, the combined process is distinctly non-Gaussian in form, having (extremely) fat tails, as shown by the QQ-plot below.
If we attempt to fit a standard ARMA model to the process, the outcome is very disappointing in terms of the model’s poor explanatory power (R2 0.5%) and lack of fit in the squared-residuals:
ARIMA(1,0,1)
Estimate Std. Err. t Ratio p-Value
Intercept 0.00037 0.00032 1.164 0.244
AR1 0.57261 0.1697 3.374 0.001
MA1 -0.63292 0.16163 -3.916 0
Error Variance^(1/2) 0.02015 0.0004 —— ——
Log Likelihood = 7451.96
Schwarz Criterion = 7435.95
Hannan-Quinn Criterion = 7443.64
Akaike Criterion = 7447.96
Sum of Squares = 1.2172
R-Squared = 0.0054
R-Bar-Squared = 0.0044
Residual SD = 0.0202
Residual Skewness = -2.1345
Residual Kurtosis = 5.7279
Jarque-Bera Test = 3206.15 {0}
Box-Pierce (residuals): Q(48) = 59.9785 {0.115}
Box-Pierce (squared residuals): Q(50) = 78.2253 {0.007}
Durbin Watson Statistic = 2.01392
KPSS test of I(0) = 0.2001 {<1} *
Lo’s RS test of I(0) = 1.2259 {<0.5} *
Nyblom-Hansen Stability Test: NH(4) = 0.5275 {<1}
MA form is 1 + a_1 L +…+ a_q L^q.
Covariance matrix from robust formula.
* KPSS, RS bandwidth = 0.
Parzen HAC kernel with Newey-West plug-in bandwidth.
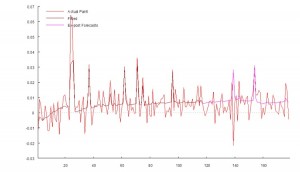
However, if we keep the same simple form of ARMA(1,1) model, but allow for the possibility of a two-state Markov process, the picture alters dramatically: now the model is able to account for 98% of the variation in the process, as shown below.
Notice that we have succeeded in estimating the correct underlying transition probabilities, and how the ARMA model parameters change from regime to regime much as they should (small positive drift in one regime, large negative drift in the second, etc).
Markov Transition Probabilities
P(.|1) P(.|2)
P(1|.) 0.080265 0.14613
P(2|.) 0.91973 0.85387
Estimate Std. Err. t Ratio p-Value
Logistic, t(1,1) -2.43875 0.1821 —— ——
Logistic, t(1,2) -1.76531 0.0558 —— ——
Non-switching parameters shown as Regime 1.
Regime 1:
Intercept -0.05615 0.00315 -17.826 0
AR1 0.70864 0.16008 4.427 0
MA1 -0.67382 0.16787 -4.014 0
Error Variance^(1/2) 0.00244 0.0001 —— ——
Regime 2:
Intercept 0.00838 2e-005 419.246 0
AR1 0.26716 0.08347 3.201 0.001
MA1 -0.26592 0.08339 -3.189 0.001
Log Likelihood = 12593.3
Schwarz Criterion = 12557.2
Hannan-Quinn Criterion = 12574.5
Akaike Criterion = 12584.3
Sum of Squares = 0.0178
R-Squared = 0.9854
R-Bar-Squared = 0.9854
Residual SD = 0.002
Residual Skewness = -0.0483
Residual Kurtosis = 13.8765
Jarque-Bera Test = 14778.5 {0}
Box-Pierce (residuals): Q(48) = 379.511 {0}
Box-Pierce (squared residuals): Q(50) = 36.8248 {0.917}
Durbin Watson Statistic = 1.50589
KPSS test of I(0) = 0.2332 {<1} *
Lo’s RS test of I(0) = 2.1352 {<0.005} *
Nyblom-Hansen Stability Test: NH(9) = 0.8396 {<1}
MA form is 1 + a_1 L +…+ a_q L^q.
Covariance matrix from robust formula.
* KPSS, RS bandwidth = 0.
Parzen HAC kernel with Newey-West plug-in bandwidth.
There are a variety of types of regime switching mechanisms we can use in state models:
Hamiltonian – the simplest, where the process mean and variance vary from state to state
Markovian – the approach used here, with state transition matrix
Explained Switching – where the process changes state as a result of the influence of some underlying variable (such as interest rate volatility, for example)
Smooth Transition – comparable to explained Markov switching, but without and explicitly probabilistic interpretation.
This example is both rather simplistic and pathological at the same time: the states are well-separated , by design, whereas for real processes they tend to be much harder to distinguish. A difficulty of this methodology is that the models can be very difficult to estimate. The likelihood function tends to be very flat and there are a great many local maxima that give similar fit, but with widely varying model forms and parameter estimates. That said, this is a very rich class of models with a great many potential applications.