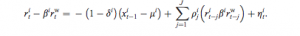Category: Factor Models

Posted on

A Two-Factor Model for Capturing Momentum and Mean Reversion in Stock Returns

Introduction:


Financial modeling has long sought to develop frameworks that accurately capture the complex dynamics of asset prices. Traditional models often focus on either momentum or mean reversion effects, struggling to incorporate both simultaneously. In this blog post, we introduce a two-factor model that aims to address this issue by integrating both momentum and mean reversion effects within the stochastic processes governing stock prices.

The Motivation Behind the Two-Factor Model:

The development of the two-factor model is motivated by the empirical observation that financial markets exhibit periods of persistent trends (momentum) and reversion to historical means or intrinsic values (mean reversion). Capturing both effects within a single framework has been a challenge in financial econometrics. The proposed model seeks to tackle this challenge by incorporating momentum and mean reversion effects within a unified framework.

The Building Blocks of the Two-Factor Model:

The two-factor model consists of two main components: a drift factor and a mean-reverting factor. The drift factor, denoted as d μ(t), represents the long-term trend or momentum of a stock’s price. It incorporates a constant drift parameter θ, reflecting the underlying direction driven by broader market forces or fundamental changes. The mean-reverting factor, denoted as d θt, captures the short-term deviations from the drift. It is characterized by a mean-reversion speed κ, which determines the rate at which prices revert to their long-term equilibrium following temporary fluctuations. These factors are influenced by their respective volatilities (σμ, σθ) and driven by correlated Wiener processes, allowing the model to reflect the interaction between momentum and mean reversion observed in markets

Empirical Application and Parameter Estimation:

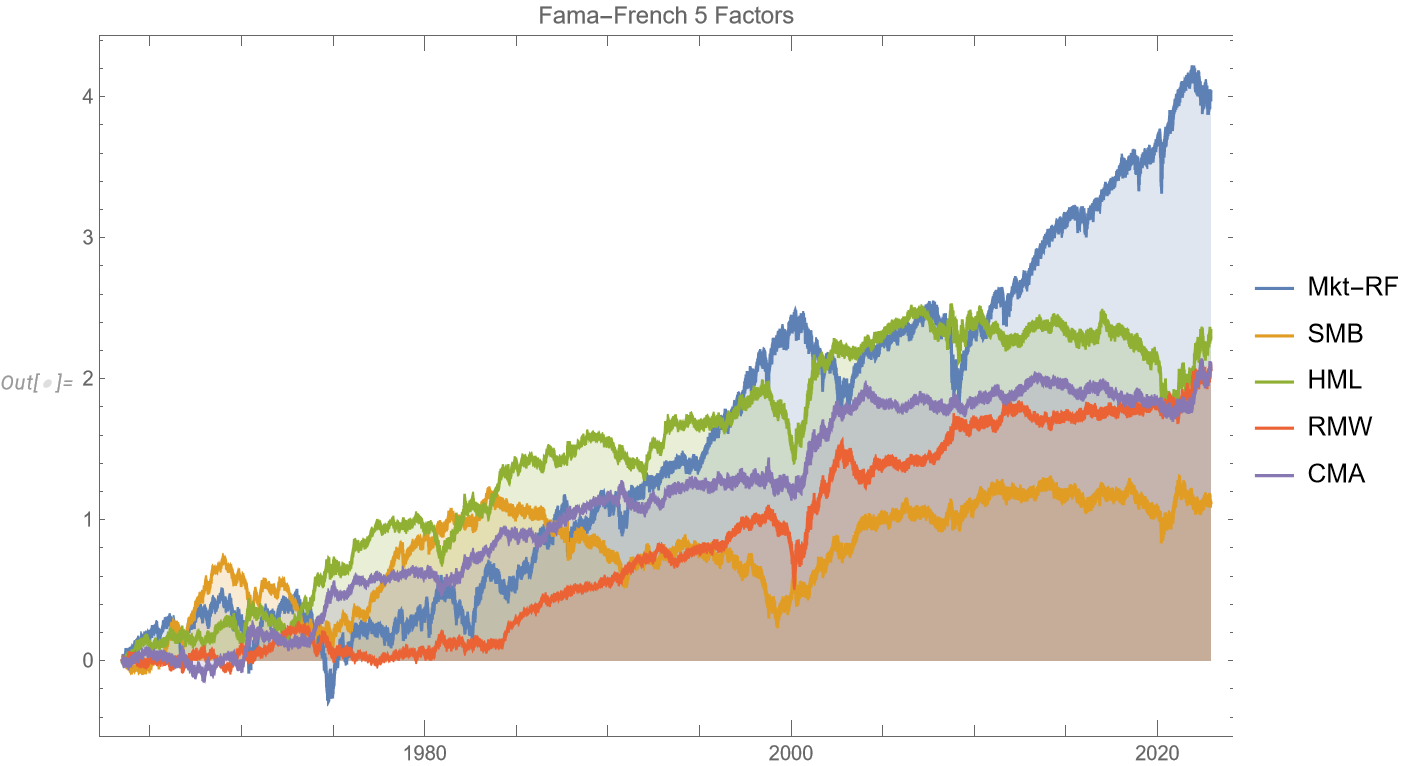
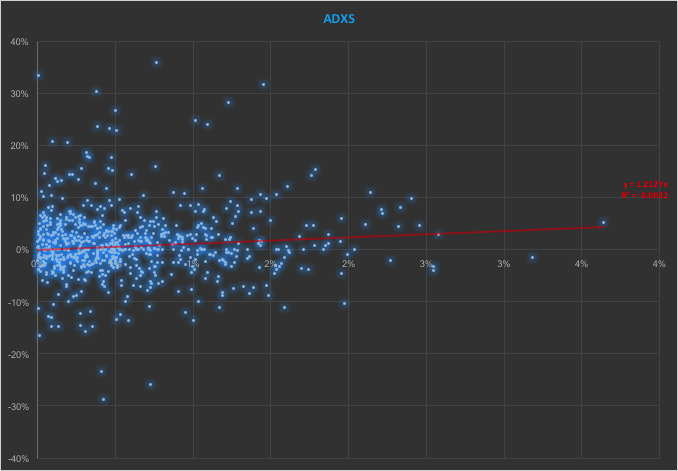
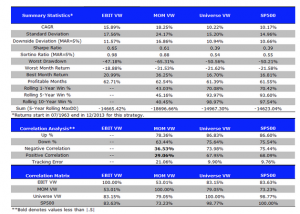
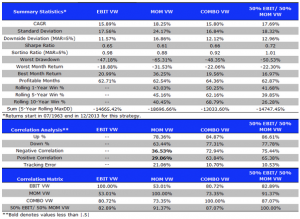
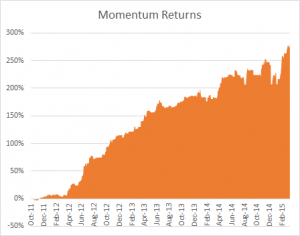
To demonstrate the model’s application, the research applies the two-factor framework to daily returns data of Coca-Cola (KO) and PepsiCo (PEP) over a twenty-year period. This empirical analysis explores the model’s potential for informing pairs trading strategies. The parameter estimation process employs a maximum likelihood estimation (MLE) technique, adapted to handle the specifics of fitting a two-factor model to real-world data. This approach aims to ensure accuracy and adaptability, enabling the model to capture the evolving dynamics of the market.

Implications for Financial Modeling and Trading Strategies:

The introduction of the two-factor model contributes to the field of quantitative finance by providing a framework that incorporates both momentum and mean reversion effects. This approach can lead to a more comprehensive understanding of asset price dynamics, potentially benefiting risk management, asset allocation, and the development of trading strategies. The model’s insights may be particularly relevant for pairs trading, where identifying relative mispricings between related assets is important.

Conclusion:

The two-factor model presented in this blog post offers a new approach to financial modeling by integrating momentum and mean reversion effects. The model’s empirical application to Coca-Cola and PepsiCo demonstrates its potential for informing trading strategies. As quantitative finance continues to evolve, the two-factor model may prove to be a useful tool for researchers, practitioners, and investors seeking to understand the dynamics of financial markets.

Two-Factor-Model-of-Stock-Returns-ver_1_1

Posted on

Beta Convexity

What is a Stock Beta?

Around a quarter of a century ago I wrote a paper entitled “Equity Convexity” which – to my disappointment – was rejected as incomprehensible by the finance professor who reviewed it.  But perhaps I should not have expected more: novel theories are rarely well received first time around.  I remain convinced the idea has merit and may perhaps revisit it in these pages at some point in future.  For now, I would like to discuss a related, but simpler concept: beta convexity.  As far as I am aware this, too, is new.  At least, while I find it unlikely that it has not already been considered, I am not aware of any reference to it in the literature.

SSALGOTRADING AD

We begin by reviewing the elementary concept of an asset beta, which is the covariance of the return of an asset with the return of the benchmark market index, divided by the variance of the return of the benchmark over a certain period:

Beta formula

Asset betas typically exhibit time dependency and there are numerous methods that can be used to model this feature, including, for instance, the Kalman Filter:

 

http://jonathankinlay.com/2015/02/statistical-arbitrage-using-kalman-filter/

Beta Convexity

In the context discussed here we set such matters to one side.  Instead of considering how an asset beta may vary over time, we look into how it might change depending on the direction of the benchmark index.  To take an example, let’s consider the stock Advaxis, Inc. (Nasdaq: ADXS).  In the charts below we examine the relationship between the daily stock returns and the returns in the benchmark Russell 3000 Index when the latter are positive and negative.

 

ADXS - Up Beta ADXS - Down Beta

 

The charts indicate that the stock beta tends to be higher during down periods in the benchmark index than during periods when the benchmark return is positive.  This can happen for two reasons: either the correlation between the asset and the index rises, or the volatility of the asset increases, (or perhaps both) when the overall market declines.  In fact, over the period from Jan 2012 to May 2017, the overall stock beta was 1.31, but the up-beta was only 0.44 while the down-beta was 1.53.  This is quite a marked difference and regardless of whether the change in beta arises from a change in the correlation or in the stock volatility, it could have a significant impact on the optimal weighting for this stock in an equity portfolio.

Ideally, what we would prefer to see is very little dependence in the relationship between the asset beta and the sign of the underlying benchmark.  One way to quantify such dependency is with what I have called Beta Convexity:

Beta Convexity = (Up-Beta – Down-Beta) ^2

A stock with a stable beta, i.e. one for which the difference between the up-beta and down-beta is negligibly small, will have a beta-convexity of zero. One the other hand, a stock that shows instability in its beta relationship with the benchmark will tend to have relatively large beta convexity.

 

Index Replication using a Minimum Beta-Convexity Portfolio

One way to apply this concept it to use it as a means of stock selection.  Regardless of whether a stock’s overall beta is large or small, ideally we want its dependency to be as close to zero as possible, i.e. with near-zero beta-convexity.  This is likely to produce greater stability in the composition of the optimal portfolio and eliminate unnecessary and undesirable excess volatility in portfolio returns by reducing nonlinearities in the relationship between the portfolio and benchmark returns.

In the following illustration we construct a stock portfolio by choosing the 500 constituents of the benchmark Russell 3000 index that have the lowest beta convexity during the previous 90-day period, rebalancing every quarter (hence all of the results are out-of-sample).  The minimum beta-convexity portfolio outperforms the benchmark by a total of 48.6% over the period from Jan 2012-May 2017, with an annual active return of 5.32% and Information Ratio of 1.36.  The portfolio tracking error is perhaps rather too large at 3.91%, but perhaps can be further reduced with the inclusion of additional stocks.

 

 

ResultsTable

 

Active Monthly

 

G1000

 

Active

Conclusion:  Beta Convexity as a New Factor

Beta convexity is a new concept that appears to have a useful role to play in identifying stocks that have stable long term dependency on the benchmark index and constructing index tracking portfolios capable of generating appreciable active returns.

The outperformance of the minimum-convexity portfolio is not the result of a momentum effect, or a systematic bias in the selection of high or low beta stocks.  The selection of the 500 lowest beta-convexity stocks in each period is somewhat arbitrary, but illustrates that the approach can scale to a size sufficient to deploy hundreds of millions of dollars of investment capital, or more.  A more sensible scheme might be, for example, to select a variable number of stocks based on a predefined tolerance limit on beta-convexity.

Obvious steps from here include experimenting with alternative weighting schemes such as value or beta convexity weighting and further refining the stock selection procedure to reduce the portfolio tracking error.

Further useful applications of the concept are likely to be found in the design of equity long/short and  market neural strategies. These I shall leave the reader to explore for now, but I will perhaps return to the topic in a future post.

Posted on

Combining Momentum and Mean Reversion Strategies

The Fama-French World

For many years now the “gold standard” in factor models has been the 1996 Fama-French 3-factor model: Fig 1
Here r is the portfolio’s expected rate of return, Rf is the risk-free return rate, and Km is the return of the market portfolio. The “three factor” β is analogous to the classical β but not equal to it, since there are now two additional factors to do some of the work. SMB stands for “Small [market capitalization] Minus Big” and HML for “High [book-to-market ratio] Minus Low”; they measure the historic excess returns of small caps over big caps and of value stocks over growth stocks. These factors are calculated with combinations of portfolios composed by ranked stocks (BtM ranking, Cap ranking) and available historical market data. The Fama–French three-factor model explains over 90% of the diversified portfolios in-sample returns, compared with the average 70% given by the standard CAPM model.

The 3-factor model can also capture the reversal of long-term returns documented by DeBondt and Thaler (1985), who noted that extreme price movements over long formation periods were followed by movements in the opposite direction. (Alpha Architect has several interesting posts on the subject, including this one).

Fama and French say the 3-factor model can account for this. Long-term losers tend to have positive HML slopes and higher future average returns. Conversely, long-term winners tend to be strong stocks that have negative slopes on HML and low future returns. Fama and French argue that DeBondt and Thaler are just loading on the HML factor.

SSALGOTRADING AD

Enter Momentum

While many anomalies disappear under  tests, shorter term momentum effects (formation periods ~1 year) appear robust. Carhart (1997) constructs his 4-factor model by using FF 3-factor model plus an additional momentum factor. He shows that his 4-factor model with MOM substantially improves the average pricing errors of the CAPM and the 3-factor model. After his work, the standard factors of asset pricing model are now commonly recognized as Value, Size and Momentum.

 Combining Momentum and Mean Reversion

In a recent post, Alpha Architect looks as some possibilities for combining momentum and mean reversion strategies.  They examine all firms above the NYSE 40th percentile for market-cap (currently around $1.8 billion) to avoid weird empirical effects associated with micro/small cap stocks. The portfolios are formed at a monthly frequency with the following 2 variables:

  1. Momentum = Total return over the past twelve months (ignoring the last month)
  2. Value = EBIT/(Total Enterprise Value)

They form the simple Value and Momentum portfolios as follows:

  1. EBIT VW = Highest decile of firms ranked on Value (EBIT/TEV). Portfolio is value-weighted.
  2. MOM VW = Highest decile of firms ranked on Momentum. Portfolio is value-weighted.
  3. Universe VW = Value-weight returns to the universe of firms.
  4. SP500 = S&P 500 Total return

The results show that the top decile of Value and Momentum outperformed the index over the past 50 years.  The Momentum strategy has stronger returns than value, on average, but much higher volatility and drawdowns. On a risk-adjusted basis they perform similarly. Fig 2   The researchers then form the following four portfolios:

  1. EBIT VW = Highest decile of firms ranked on Value (EBIT/TEV). Portfolio is value-weighted.
  2. MOM VW = Highest decile of firms ranked on Momentum. Portfolio is value-weighted.
  3. COMBO VW = Rank firms independently on both Value and Momentum.  Add the two rankings together. Select the highest decile of firms ranked on the combined rankings. Portfolio is value-weighted.
  4. 50% EBIT/ 50% MOM VW = Each month, invest 50% in the EBIT VW portfolio, and 50% in the MOM VW portfolio. Portfolio is value-weighted.

With the following results:

Fig 3 The main takeaways are:

  • The combined ranked portfolio outperforms the index over the same time period.
  • However, the combination portfolio performs worse than a 50% allocation to Value and a 50% allocation to Momentum.

A More Sophisticated Model

Yangru Wu of Rutgers has been doing interesting work in this area over the last 15 years, or more. His 2005 paper (with Ronald Balvers), Momentum and mean reversion across national equity markets, considers joint momentum and mean-reversion effects and allows for complex interactions between them. Their model is of the form Fig 4 where the excess return for country i (relative to the global equity portfolio) is represented by a combination of mean-reversion and autoregressive (momentum) terms. Balvers and Wu  find that combination momentum-contrarian strategies, used to select from among 18 developed equity markets at a monthly frequency, outperform both pure momentum and pure mean-reversion strategies. The results continue to hold after corrections for factor sensitivities and transaction costs. The researchers confirm that momentum and mean reversion occur in the same assets. So in establishing the strength and duration of the momentum and mean reversion effects it becomes important to control for each factor’s effect on the other. The momentum and mean reversion effects exhibit a strong negative correlation of 35%. Accordingly, controlling for momentum accelerates the mean reversion process, and controlling for mean reversion may extend the momentum effect.

 Momentum, Mean Reversion and Volatility

The presence of  strong momentum and mean reversion in volatility processes provides a rationale for the kind of volatility strategy that we trade at Systematic Strategies.  One  sophisticated model is the Range Based EGARCH model of  Alizadeh, Brandt, and Diebold (2002) .  The model posits a two-factor volatility process in which a short term, transient volatility process mean-reverts to a stochastic long term mean process, which may exhibit momentum, or long memory effects  (details here).

In our volatility strategy we model mean reversion and momentum effects derived from the level of short and long term volatility-of-volatility, as well as the forward volatility curve. These are applied to volatility ETFs, including levered ETF products, where convexity effects are also important.  Mean reversion is a well understood phenomenon in volatility, as, too, is the yield roll in volatility futures (which also impacts ETF products like VXX and XIV).

Momentum effects are perhaps less well researched in this context, but our research shows them to be extremely important.  By way of illustration, in the chart below I have isolated the (gross) returns generated by one of the momentum factors in our model.

Fig 6