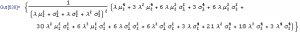Category: Volatility

Posted on

Volatility ETF Trader – June 2017: +15.3%

The Volatility ETF Trader product is an algorithmic strategy that trades several VIX ETFs using statistical and machine learning algorithms.

We offer a version of the strategy on the Collective 2 site (see here for details) that the user can subscribe to for a very modest fee of only $149 per month.

The risk-adjusted performance of the Collective 2 version of the strategy is unlikely to prove as good as the product we offer in our Systematic Strategies Fund, which trades a much wider range of algorithmic strategies.  There are other important differences too:  the Fund’s Systematic Volatility Strategy makes no use of leverage and only trades intra-day, exiting all positions by market close.  So it has a more conservative risk profile, suitable for longer term investment.

The Volatility ETF Trader on Collective 2, on the other hand, is a highly leveraged, tactical strategy that trades positions overnight and holds them for periods of several days .  As a consequence, the Collective 2 strategy is far more risky and is likely to experience significant drawdowns.    Those caveats aside, the strategy returns have been outstanding:  +48.9% for 2017 YTD and a total of +107.8% from inception in July 2016.

You can find full details of the strategy, including a listing of all of the trades, on the Collective 2 site.

Subscribers can sign up for a free, seven day trial and thereafter they can choose to trade the strategy automatically in their own brokerage account.

 

VIX ETF Strategy June 2017

Posted on

Algorithmic Trading on Collective 2


Regular readers will recall my mentioning out VIX Futures scalping strategy which we ran on the Collective2 site for a while:

 

VIX HFT Scalper

 

The strategy, while performing very well, proved difficult for subscribers to implement, given the latencies involved in routing orders via the Collective 2 web site.  So we began thinking about slower strategies that investors could follow more easily, placing less reliance on the fill rate for limit orders.

Our VIX ETF Trader strategy has been running on Collective 2 for several months now and is being traded successfully by several subscribers.  The performance so far has been quite good, with net returns of 58.9% from July 2016 and a Sharpe ratio over 2, which is not at all bad for a low frequency strategy.  The strategy enters and exits using a mix of  limit and stop orders, so although some slippage is incurred the trade entries and exits work much more smoothly overall.

Having let the strategy settle for several months trading only the ProShares Short VIX Short-Term Futures ETF (SVXY)we are now ready to ramp things up.  From today the strategy will also trade several other VIX ETF products including the VelocityShares Daily Inverse VIX ST ETN (XIV), ProShares Ultra VIX Short-Term Futures (UVXY) and VelocityShares Daily 2x VIX ST ETN (TVIX).  All of the trades in these products are entered and exited using market or stop orders, and so will be easy for subscribers to follow.  For now we are keeping the required account size pegged at $25,000 although we will review that going forward.  My guess is that a capital allocation should be more than sufficient to trade the product in the kind of size we use on the Collective 2 versions of the strategies, especially if the account uses portfolio margin rather than standard Reg-T.

With the addition of the new products to the portfolio mix, we anticipate the strategy Sharpe ratio with rise to over 3 in the year ahead.

 

 

VIX ETF Strategy

 

The advantage of using a site like Collective 2 from the investor’s viewpoint is that, firstly, you get to see a lot of different trading styles and investment strategies.  You can select the strategies in a wide range of asset classes that fit your own investment preferences and trade several of them live in your own brokerage account.  (Setting up your account for live trading is straightforward, as described on the C2 site).  A major advantage of investing this way is that it doesn’t entail the commitment of capital that is typically required for a hedge fund or managed account investment:  you can trade the strategies in much smaller size, to fit your budget.

From our perspective, we find it a useful way to showcase some of the strategies we trade in our hedge fund, so that if investors want to they can move up to more advanced, but similar investment products.  We plan to launch new strategies on Collective 2 in the near futures , including an equity portfolio strategy and a CTA futures strategy.

If you would like more information, contact us for further details.

 

Posted on

Ethical Strategy Design

It isn’t often that you see an equity curve like the one shown below, which was produced by a systematic strategy built on 1-minute bars in the ProShares Ultra VIX Short-Term Futures ETF (UVXY):
 Fig3

As the chart indicates, the strategy is very profitable, has a very high overall profit factor and a trade win rate in excess of 94%:

Fig4

 

FIG5

 

So, what’s not to like?  Well, arguably, one would like to see a strategy with a more balanced P&L, capable of producing profitable trades on the long as well as the short side. That would give some comfort that the strategy will continue to perform well regardless of whether the market tone is bullish or bearish. That said, it is understandable that the negative drift from carry in volatility futures, amplified by the leverage in the leveraged ETF product, makes it is much easier to make money by selling short.  This is  analogous to the long bias in the great majority of equity strategies, which relies on the positive drift in stocks.  My view would be that the short bias in the UVXY strategy is hardly a sufficient reason to overlook its many other very attractive features, any more than long bias is a reason to eschew equity strategies.

SSALGOTRADING AD

This example is similar to one we use in our training program for proprietary and hedge fund traders, to illustrate some of the pitfalls of strategy development.  We point out that the strategy performance has held up well out of sample – indeed, it matches the in-sample performance characteristics very closely.  When we ask trainees how they could test the strategy further, the suggestion is often made that we use Monte-Carlo simulation to evaluate the performance across a wider range of market scenarios than seen in the historical data.  We do this by introducing random fluctuations into the ETF prices, as well as in the strategy parameters, and by randomizing the start date of the test period.  The results are shown below. As you can see, while there is some variation in the strategy performance, even the worst simulated outcome appears very benign.

 

Fig2

Around this point trainees, at least those inexperienced in trading system development, tend to run out of ideas about what else could be done to evaluate the strategy.  One or two will mention drawdown risk, but the straight-line equity curve indicates that this has not been a problem for the strategy in the past, while the results of simulation testing suggest that drawdowns are unlikely to be a significant concern, across a broad spectrum of market conditions.  Most trainees simply want to start trading the strategy as soon as possible (although the more cautious of them will suggest trading in simulation mode for a while).

As this point I sometimes offer to let trainees see the strategy code, on condition that they agree to trade the strategy with their own capital.   Being smart people, they realize something must be wrong, even if they are unable to pinpoint what the problem may be.  So the discussion moves on to focus in more detail the question of strategy risk.

A Deeper Dive into Strategy Risk

At this stage I point out to trainees that the equity curve shows the result from realized gains and losses. What it does not show are the fluctuations in equity that occurred before each trade was closed.

That information is revealed by the following report on the maximum adverse excursion (MAE), which plots the maximum drawdown in each trade vs. the final trade profit or loss.  Once trainees understand the report, the lights begin to come on.  We can see immediately that there were several trades which were underwater to the tune of $30,000, $50,000, or even $70,000 , or more, before eventually recovering to produce a profit.  In the most extreme case the trade was almost $80,000 underwater, before producing a profit of only a few hundred dollars. Furthermore, the drawdown period lasted for several weeks, which represents almost geological time for a strategy operating on 1-minute bars. It’s not hard to grasp the concept that risking $80,000 of your own money in order to make $250 is hardly an efficient use of capital, or an acceptable level of risk-reward.


 FIG6 FIG7

 

FIG8

 

Next, I ask for suggestions for how to tackle the problem of drawdown risk in the strategy.   Most trainees will suggest implementing a stop-loss strategy, similar to those employed by thousands of  trading firms.  Looking at the MAE chart, it appears that we can avert the worst outcomes with a stop loss limit of, say, $25,000.  However, when we implement a stop loss strategy at this level, here’s the outcome it produces:

 

FIG9

Now we see the difficulty.  Firstly, what a stop-loss strategy does is simply crystallize the previously unrealized drawdown losses.  Consequently, the equity curve looks a great deal less attractive than it did before.  The second problem is more subtle: the conditions that produced the loss-making trades tend to continue for some time, perhaps as long as several days, or weeks.  So, a strategy that has a stop loss risk overlay will tend to exit the existing position, only to reinstate a similar position more or less immediately.  In other words, a stop loss achieves very little, other than to force the trader to accept losses that the strategy would have made up if it had been allowed to continue.  This outcome is a difficult one to accept, even in the face of the argument that a stop loss serves the purpose of protecting the trader (and his firm) from an even more catastrophic loss.  Because if the strategy tends to re-enter exactly the same position shortly after being stopped out, very little has been gained in terms of catastrophic risk management.

Luck and the Ethics of Strategy Design

What are the learning points from this exercise in trading system development?  Firstly, one should resist being beguiled by stellar-looking equity curves: they may disguise the true risk characteristics of the strategy, which can only be understood by a close study of strategy drawdowns and  trade MAE.  Secondly, a lesson that many risk managers could usefully take away is that a stop loss is often counter-productive, serving only to cement losses that the strategy would otherwise have recovered from.

A more subtle point is that a Geometric Brownian Motion process has a long-term probability of reaching any price level with certainty.  Accordingly, in theory one has only to wait long enough to recover from any loss, no matter how severe.   Of course, in the meantime, the accumulated losses might be enough to decimate the trading account, or even bring down the entire firm (e.g. Barings).  The point is,  it is not hard to design a system with a very seductive-looking backtest performance record.

If the solution is not a stop loss, how do we avoid scenarios like this one?  Firstly, if you are trading someone else’s money, one answer is: be lucky!  If you happened to start trading this strategy some time in 2016, you would probably be collecting a large bonus.  On the other hand, if you were unlucky enough to start trading in early 2017, you might be collecting a pink slip very soon.  Although unethical, when you are gambling with other people’s money, it makes economic sense to take such risks, because the potential upside gain is so much greater than the downside risk (for you). When you are risking with your own capital, however, the calculus is entirely different.  That is why we always trade strategies with our own capital before opening them to external investors (and why we insist that our prop traders do the same).

As a strategy designer, you know better, and should act accordingly.  Investors, who are relying on your skills and knowledge, can all too easily be seduced by the appearance of a strategy’s outstanding performance, overlooking the latent risks it hides.  We see this over and over again in option-selling strategies, which investors continue to pile into despite repeated demonstrations of their capital-destroying potential.  Incidentally, this is not a point about backtest vs. live trading performance:  the strategy illustrated here, as well as many option-selling strategies, are perfectly capable of producing live track records similar to those seen in backtest.  All you need is some luck and an uneventful period in which major drawdowns don’t arise.  At Systematic Strategies, our view is that the strategy designer is under an obligation to shield his investors from such latent risks, even if they may be unaware of them.  If you know that a strategy has such risk characteristics, you should avoid it, and design a better one.  The risk controls, including limitations on unrealized drawdowns (MAE) need to be baked into the strategy design from the outset, not fitted retrospectively (and often counter-productively, as we have seen here).

The acid test is this:  if you would not be prepared to risk your own capital in a strategy, don’t ask your investors to take the risk either.

The ethical principle of “do unto others as you would have them do unto you” applies no less in investment finance than it does in life.

Strategy Code

Code for UVXY Strategy

 

Posted on

Modeling Asset Processes

Introduction

Over the last twenty five years significant advances have been made in the theory of asset processes and there now exist a variety of mathematical models, many of them computationally tractable, that provide a reasonable representation of their defining characteristics.

SSALGOTRADING AD

While the Geometric Brownian Motion model remains a staple of stochastic calculus theory, it is no longer the only game in town.  Other models, many more sophisticated, have been developed to address the shortcomings in the original.  There now exist models that provide a good explanation of some of the key characteristics of asset processes that lie beyond the scope of models couched in a simple Gaussian framework. Features such as mean reversion, long memory, stochastic volatility,  jumps and heavy tails are now readily handled by these more advanced tools.

In this post I review a critical selection of asset process models that belong in every financial engineer’s toolbox, point out their key features and limitations and give examples of some of their applications.

Modeling Asset Processes

Posted on

Crash-Proof Investing

As markets continue to make new highs against a backdrop of ever diminishing participation and trading volume, investors have legitimate reasons for being concerned about prospects for the remainder of 2016 and beyond, even without consideration to the myriad of economic and geopolitical risks that now confront the US and global economies. Against that backdrop, remaining fully invested is a test of nerves for those whose instinct is that they may be picking up pennies in front an oncoming steamroller.  On the other hand, there is a sense of frustration in cashing out, only to watch markets surge another several hundred points to new highs.

In this article I am going to outline some steps investors can take to match their investment portfolios to suit current market conditions in a way that allows them to remain fully invested, while safeguarding against downside risk.  In what follows I will be using our own Strategic Volatility Strategy, which invests in volatility ETFs such as the iPath S&P 500 VIX ST Futures ETN (NYSEArca:VXX) and the VelocityShares Daily Inverse VIX ST ETN (NYSEArca:XIV), as an illustrative example, although the principles are no less valid for portfolios comprising other ETFs or equities.

SSALGOTRADING AD

Risk and Volatility

Risk may be defined as the uncertainty of outcome and the most common way of assessing it in the context of investment theory is by means of the standard deviation of returns.  One difficulty here is that one may never ascertain the true rate of volatility – the second moment – of a returns process; one can only estimate it.  Hence, while one can be certain what the closing price of a stock was at yesterday’s market close, one cannot say what the volatility of the stock was over the preceding week – it cannot be observed the way that a stock price can, only estimated.  The most common estimator of asset volatility is, of course, the sample standard deviation.  But there are many others that are arguably superior:  Log-Range, Parkinson, Garman-Klass to name but a few (a starting point for those interested in such theoretical matters is a research paper entitled Estimating Historical Volatility, Brandt & Kinlay, 2005).

Leaving questions of estimation to one side, one issue with using standard deviation as a measure of risk is that it treats upside and downside risk equally – the “risk” that you might double your money in an investment is regarded no differently than the risk that you might see your investment capital cut in half.  This is not, of course, how investors tend to look at things: they typically allocate a far higher cost to downside risk, compared to upside risk.

One way to address the issue is by using a measure of risk known as the semi-deviation.  This is estimated in exactly the same way as the standard deviation, except that it is applied only to negative returns.  In other words, it seeks to isolate the downside risk alone.

This leads directly to a measure of performance known as the Sortino Ratio.  Like the more traditional Sharpe Ratio, the Sortino Ratio is a measure of risk-adjusted performance – the average return produced by an investment per unit of risk.  But, whereas the Sharpe Ratio uses the standard deviation as the measure of risk, for the Sortino Ratio we use the semi-deviation. In other words, we are measuring the expected return per unit of downside risk.

There may be a great deal of variation in the upside returns of a strategy that would penalize the risk-adjusted returns, as measured by its Sharpe Ratio. But using the Sortino Ratio, we ignore the upside volatility entirely and focus exclusively on the volatility of negative returns (technically, the returns falling below a given threshold, such as the risk-free rate.  Here we are using zero as our benchmark).  This is, arguably, closer to the way most investors tend to think about their investment risk and return preferences.

In a scenario where, as an investor, you are particularly concerned about downside risk, it makes sense to focus on downside risk.  It follows that, rather than aiming to maximize the Sharpe Ratio of your investment portfolio, you might do better to focus on the Sortino Ratio.

 

Factor Risk and Correlation Risk

Another type of market risk that is often present in an investment portfolio is correlation risk.  This is the risk that your investment portfolio correlates to some other asset or investment index.  Such risks are often occluded – hidden from view – only to emerge when least wanted.  For example, it might be supposed that a “dollar-neutral” portfolio, i.e. a portfolio comprising equity long and short positions of equal dollar value, might be uncorrelated with the broad equity market indices.  It might well be.  On the other hand, the portfolio might become correlated with such indices during times of market turbulence; or it might correlate positively with some sector indices and negatively with others; or with market volatility, as measured by the CBOE VIX index, for instance.

Where such dependencies are included by design, they are not a problem;  but when they are unintended and latent in the investment portfolio, they often create difficulties.  The key here is to test for such dependencies against a variety of risk factors that are likely to be of concern.  These might include currency and interest rate risk factors, for example;  sector indices; or commodity risk factors such as oil or gold (in a situation where, for example, you are investing a a portfolio of mining stocks).  Once an unwanted correlation is identified, the next step is to adjust the portfolio holdings to try to eliminate it.  Typically, this can often only be done in the average, meaning that, while there is no correlation bias over the long term, there may be periods of positive, negative, or alternating correlation over shorter time horizons.  Either way, it’s important to know.

Using the Strategic Volatility Strategy as an example, we target to maximize the Sortino Ratio, subject also to maintaining very lows levels of correlation to the principal risk factors of concern to us, the S&P 500 and VIX indices. Our aim is to create a portfolio that is broadly impervious to changes in the level of the overall market, or in the level of market volatility.

 

One method of quantifying such dependencies is with linear regression analysis.  By way of illustration, in the table below are shown the results of regressing the daily returns from the Strategic Volatility Strategy against the returns in the VIX and S&P 500 indices.  Both factor coefficients are statistically indistinguishable from zero, i.e. there is significant no (linear) dependency.  However, the constant coefficient, referred to as the strategy alpha, is both positive and statistically significant.  In simple terms, the strategy produces a return that is consistently positive, on average, and which is not dependent on changes in the level of the broad market, or its volatility.  By contrast, for example, a commonplace volatility strategy that entails capturing the VIX futures roll would show a negative correlation to the VIX index and a positive dependency on the S&P500 index.

Regression

 

Tail Risk

Ever since the publication of Nassim Taleb’s “The Black Swan”, investors have taken a much greater interest in the risk of extreme events.  If the bursting of the tech bubble in 2000 was not painful enough, investors surely appear to have learned the lesson thoroughly after the financial crisis of 2008.  But even if investors understand the concept, the question remains: what can one do about it?

The place to start is by looking at the fundamental characteristics of the portfolio returns.  Here we are not such much concerned with risk, as measured by the second moment, the standard deviation. Instead, we now want to consider the third and forth moments of the distribution, the skewness and kurtosis.

Comparing the two distributions below, we can see that the distribution on the left, with negative skew, has nonzero probability associated with events in the extreme left of the distribution, which in this context, we would associate with negative returns.  The distribution on the right, with positive skew, is likewise “heavy-tailed”; but in this case the tail “risk” is associated with large, positive returns.  That’s the kind of risk most investors can live with.

 

skewness

 

Source: Wikipedia

 

 

A more direct measure of tail risk is kurtosis, literally, “heavy tailed-ness”, indicating a propensity for extreme events to occur.  Again, the shape of the distribution matters:  a heavy tail in the right hand portion of the distribution is fine;  a heavy tail on the left (indicating the likelihood of large, negative returns) is a no-no.

Let’s take a look at the distribution of returns for the Strategic Volatility Strategy.  As you can see, the distribution is very positively skewed, with a very heavy right hand tail.  In other words, the strategy has a tendency to produce extremely positive returns. That’s the kind of tail risk investors prefer.

SVS

 

Another way to evaluate tail risk is to examine directly the performance of the strategy during extreme market conditions, when the market makes a major move up or down. Since we are using a volatility strategy as an example, let’s take a look at how it performs on days when the VIX index moves up or down by more than 5%.  As you can see from the chart below, by and large the strategy returns on such days tend to be positive and, furthermore, occasionally the strategy produces exceptionally high returns.

 

Convexity

 

The property of producing higher returns to the upside and lower losses to the downside (or, in this case, a tendency to produce positive returns in major market moves in either direction) is known as positive convexity.

 

Positive convexity, more typically found in fixed income portfolios, is a highly desirable feature, of course.  How can it be achieved?    Those familiar with options will recognize the convexity feature as being similar to the concept of option Gamma and indeed, one way to produce such a payoff is buy adding options to the investment mix:  put options to give positive convexity to the downside, call options to provide positive convexity to the upside (or using a combination of both, i.e. a straddle).

 

In this case we achieve positive convexity, not by incorporating options, but through a judicious choice of leveraged ETFs, both equity and volatility, for example, the ProShares UltraPro S&P500 ETF (NYSEArca:UPRO) and the ProShares Ultra VIX Short-Term Futures ETN (NYSEArca:UVXY).

 

Putting It All Together

While we have talked through the various concepts in creating a risk-protected portfolio one-at-a-time, in practice we use nonlinear optimization techniques to construct a portfolio that incorporates all of the desired characteristics simultaneously. This can be a lengthy and tedious procedure, involving lots of trial and error.  And it cannot be emphasized enough how important the choice of the investment universe is from the outset.  In this case, for instance, it would likely be pointless to target an overall positively convex portfolio without including one or more leveraged ETFs in the investment mix.

Let’s see how it turned out in the case of the Strategic Volatility Strategy.

 

SVS Perf

 

 

Note that, while the portfolio Information Ratio is moderate (just above 3), the Sortino Ratio is consistently very high, averaging in excess of 7.  In large part that is due to the exceptionally low downside risk, which at 1.36% is less than half the standard deviation (which is itself quite low at 3.3%).  It is no surprise that the maximum drawdown over the period from 2012 amounts to less than 1%.

A critic might argue that a CAGR of only 10% is rather modest, especially since market conditions have generally been so benign.  I would answer that criticism in two ways.  Firstly, this is an investment that has the risk characteristics of a low-duration government bond; and yet it produces a yield many times that of a typical bond in the current low interest rate environment.

Secondly, I would point out that these results are based on use of standard 2:1 Reg-T leverage. In practice it is entirely feasible to increase the leverage up to 4:1, which would produce a CAGR of around 20%.  Investors can choose where on the spectrum of risk-return they wish to locate the portfolio and the strategy leverage can be adjusted accordingly.

 

Conclusion

The current investment environment, characterized by low yields and growing downside risk, poses difficult challenges for investors.  A way to address these concerns is to focus on metrics of downside risk in the construction of the investment portfolio, aiming for high Sortino Ratios, low correlation with market risk factors, and positive skewness and convexity in the portfolio returns process.

Such desirable characteristics can be achieved with modern portfolio construction techniques providing the investment universe is chosen carefully and need not include anything more exotic than a collection of commonplace ETF products.

Posted on

Quantitative Analysis of Fat Tails – JonathanKinlay.com

In this quantitative analysis I explore how, starting from the assumption of a stable, Gaussian distribution in a returns process, we evolve to a system that displays all the characteristics of empirical market data, notably time-dependent moments, high levels of kurtosis and fat tails.  As it turns out, the only additional assumption one needs to make is that the market is periodically disturbed by the random arrival of news.

NOTE:  if you are unable to see the Mathematica models below, you can download the free Wolfram CDF player and you may also need this plug-in.

You can also download the complete Mathematica CDF file here.

Stationarity

A stationary process is one that evolves over time, but whose probability distribution does not vary with time. As the word implies, such a process is stable. More formally, the moments of the distribution are independent of time.

Let’s assume we are dealing with such a process that have constant mean μ and constant volatility (standard deviation) σ.

 Φ=NormalDistribution[μ,σ]

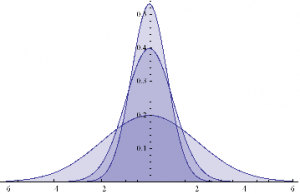
Here are some examples of Normal probability distributions, with constant mean μ = 0 and standard deviation σ ranging from 0.75 to 2

 Plot[Evaluate@Table[PDF[Φ,x],{σ,{.75,1,2}}]/.μ→0,{x,-6,6},Filling→Axis]

 

Chart 1

The moments of Φ are given by:

 Through[{Mean, StandardDeviation, Skewness, Kurtosis}[Φ]]

{μ,  σ,  0,   3}

They, too, are time – independent.

We can simulate some observations from such a process, with, say, mean μ = 0 and standard deviation σ = 1:

ListPlot[sampleData=RandomVariate[Φ /.{μ→0, σ→1},10^4]]

 

Chart 2

Histogram[sampleData]

Chart 3

If we assume for the moment that such a process is an adequate description of an asset returns process, we can simulate the evolution of a price process as follows :

ListPlot[prices=Accumulate[sampleData]]

Chart 4

 

SSALGOTRADING AD

An Empirical Distribution

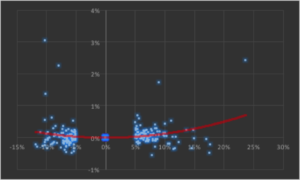
Lets take a look at a real price series, comprising 1 – minute bar data in the June ‘ 14 E – Mini futures contract.

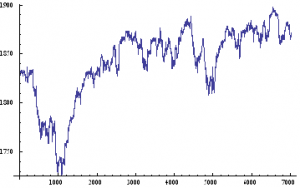
Chart 5

As with our simulated price process, it is clear that the real price process for Emini futures is also non – stationary.

What about the returns process?

ListPlot[returnsES]

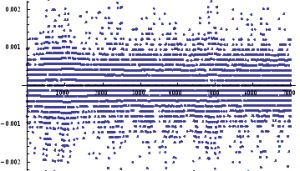
Chart 6

Notice the banding effect in returns, which results from having a fixed, minimum price move of $12 .50, rather than a continuous scale.

Histogram[returnsES]

 

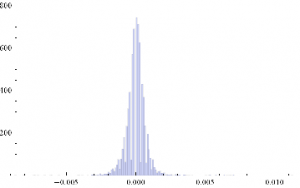
Chart 7

Through[{Min,Max,Mean,Median,StandardDeviation,Skewness,Kurtosis}[returnsES]]

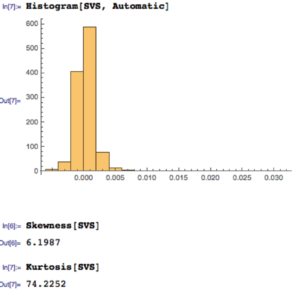
{-0.00867214,  0.0112353,  2.75501×10-6,   0.,   0.000780895,   0.35467,   26.2376}

The empirical returns distribution doesn’ t appear to be Gaussian – the distribution is much more peaked than a standard Normal distribution with the same mean and standard deviation. And the higher moments don’t fit the Normal model either – the empirical distribution has positive skew and a kurtosis that is almost 9x greater than a Gaussian distribution. The latter signifies what is often referred to as “fat tails”: the distribution has much greater weight in the tails than a standard Normal distribution, indicating a much greater likelihood of an extreme value than a Normal distribution would predict.

A Quantitative Analysis of Non-Stationarity: Two States

Non – stationarity arises when one or more of the moments of a distribution vary over time. Let’s take a look at how that can arise, and its effects.Suppose we have a Gaussian returns process for which the mean, or drift, or trend, fluctuates over time.

Let’s consider a simple example where the process drift is  μ1 and volatility σ1 for most of the time and then for some proportion of time k, we get addition drift  μ2 and volatility σ2.  In other words we have:

 Φ1=NormalDistribution[μ1,σ1]

 Through[{Mean,StandardDeviation,Skewness,Kurtosis}[Φ1]]

{μ1,   σ1,   0,   3}

 Φ2=NormalDistribution[μ2,σ2]

 Through[{Mean,StandardDeviation,Skewness,Kurtosis}[Φ2]]

{μ2,   σ2,   0,   3}

This simple model fits a scenario in which we suppose that the returns process spends most of its time in State 1, in which is Normally distributed with  drift is  μ1 and volatility σ1, and suffers from the occasional “shock” which propels the systems into a second State 2, in which its distribution is a combination of its original distribution and a new Gaussian distribution with different mean and volatility.

Let’ s suppose that we sample the combined process y =  Φ1 + k  Φ2.   What distribution would it have?  We can represent this is follows :

 y=TransformedDistribution[(x1+k x2),{x1~Φ1,x2~Φ2}]


Eqn2 

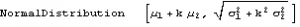
 Through[{Mean,StandardDeviation,Skewness,Kurtosis}[y]]

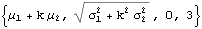
Stationarity_52

 Plot[PDF[y,x]/.{μ1→0,μ2→0,σ1 →1,σ2 →2, k→0.5},{x,-6,6},Filling→Axis]

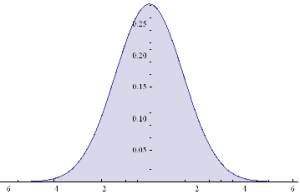
Chart 8

The result is just another Normal distribution. Depending on the incidence k, y will follow a Gaussian distribution whose mean and variance depend on the mean and variance of the two Normal distributions being mixed. The resulting distribution in State 2 may have higher or lower drift and volatility, but it is still Gaussian, with constant kurtosis of 3.

In other words, the system y will be non-stationary, because the first and second moments change over time, depending on what state it is in. But the form of the distribution is unchanged – it is still Gaussian. There are no fat-tails.

Non – Stationarity : Random States

In the above example the system moved between states in a known, predictable way. The “shocks” to the system were not really shocks, but transitions. But that’s not how financial markets behave: markets move from one state to another in an unpredictable way, with the arrival of news.

We can simulate this situation as follows. Using the former model as a starting point, lets now relax the assumption that the incidence of the second state, k, is a constant. Instead, let’ s assume that k is itself a random variable. In other words we are going to now assume that our system changes state in a random way. How does this alter the distribution?

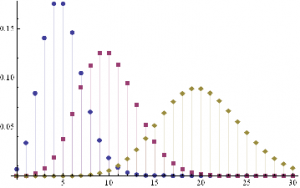
An appropriate model for λ might be a Poisson process, which is often used as a model for unpredictable, discrete events, ranging from bus arrivals to earthquakes.  PDFs of Poisson distributions with means  λ=5, 10 and 20 are shown in the chart below.  These represent probability distributions for processes that have mean  arrivals of 5, 10 or 20 events.

 DiscretePlot[Evaluate@Table[PDF[PoissonDistribution[λ],k],{λ,{5,10,20}}],{k,0,30},PlotRange→All,PlotMarkers→Automatic]

Chart 9

Our new model now looks like this :

 y=TransformedDistribution[{x1+k*x2},{x1⎡Φ1,x2⎡Φ2,k⎡PoissonDistribution[λ]}]

The first two moments of the distribution are as follows :

Through[{Mean,StandardDeviation}[y]]

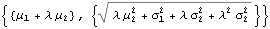
Stationarity_60

As before, the mean and standard deviation of the distribution are going to vary, depending on the state of the system, and the mean arrival rate of shocks, . But what about kurtosis? Is it still constant?

Kurtosis[y]

Eqn1

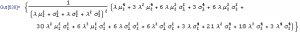
Emphatically not!  The fourth moment of the distribution is now dependent on the drift in the second state, the volatilities of both states and the mean arrival rate of shocks, λ.

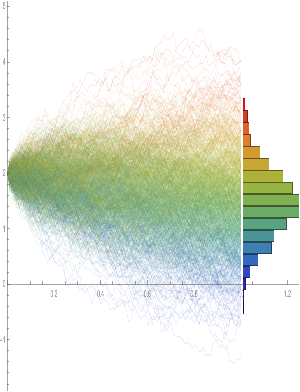
Let’ s look at a specific example.  Assume that in State 1 the process has volatility of 7.5 %, with zero drift, and that the shock distribution also has zero drift with volatility of 65 %. If the mean incidence rate of shocks λ = 10 %, the distribution kurtosis is close to that seen in the empirical distribution for the E-Mini.

 Kurtosis[y] /.{σ1→0.075,μ2→0,σ2→0.65,λ→0.1}

{35.3551}

More generally :

 ListLinePlot[Flatten[Kurtosis[y]/.Table[{σ1→0.075,μ2→0,σ2→0.65,λ→i/20},{i,1,20}]],PlotLabel→Style[“Kurtosis vs Mean Shock Arrival Rate”, FontSize→18],AxesLabel->{“Incidence Rate (%)”, “Kurtosis”},Filling→Axis, ImageSize→Large]

 

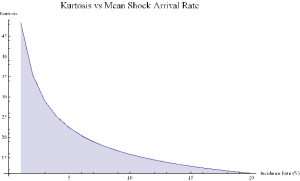
Chart 10

Thus we can see how, even if the underlying returns distribution is Gaussian in form, the random arrival of news “shocks” to the system can induce non – stationarity in overall drift and volatility. It can also result in fat tails. More specifically, if the arrival of news is stochastic in nature, rather than deterministic, the process may exhibit far higher levels of kurtosis than in its original Gaussian state, in which the fourth moment was a constant level of 3.

Quantitative Analysis of a Jump Diffusion Process

Nobel – prize winning economist Robert Merton extended this basic concept to the realm of stochastic calculus.

In Merton’s jump diffusion model, the stock price follows the random process

∂St / St =μdt + σdWt+(J-1)dNt

The first two terms are familiar from the Black–Scholes model : drift rate μ, volatility σ, and random walk Wt (Wiener process).The last term represents the jumps :J is the jump size as a multiple of stock price, while Nt is the number of jump events that have occurred up to time t.is assumed to follow the Poisson process.

 PDF[PoissonDistribution[λt]]

where λ is the average frequency with which jumps occur.

The jump size J follows a log – normal distribution

 PDF[LogNormalDistribution[m, ν], s]

where m is the average jump size and v is the volatility of the jump size.

In the jump diffusion model, the stock price St follows the random process dSt/St=μ dt+σ dWt+(J-1) dN(t), which comprises, in order, drift, diffusive, and jump components. The jumps occur according to a Poisson distribution and their size follows a log-normal distribution. The model is characterized by the diffusive volatility σ, the average jump size J (expressed as a fraction of St), the frequency of jumps λ, and the volatility of jump size ν.

The Volatility Smile

The “implied volatility” corresponding to an option price is the value of the volatility parameter for which the Black-Scholes model gives the same price. A well-known phenomenon in market option prices is the “volatility smile”, in which the implied volatility increases for strike values away from the spot price. The jump diffusion model is a generalization of Black–Scholes in which the stock price has randomly occurring jumps in addition to the random walk behavior. One of the interesting properties of this model is that it displays the volatility smile effect. In this Demonstration, we explore the Black–Scholes implied volatility of option prices (equal for both put and call options) in the jump diffusion model. The implied volatility is modeled as a function of the ratio of option strike price to spot price.