For those who prefer a little more rigor in their quantitative research, I can offer more a somewhat more substantive statistical argument in favor of the IBS indicator discussed in my previous post.
Specifically, we can show quite convincingly that the IBS process is stationary, a highly desirable property much sought-after in, for example, the construction of statistical arbitrage strategies. Of course, by construction, the IBS is constrained to lie between the values of 0 and 1, so non-stationarity in the mean is highly unlikely. But, conceivably, there could be some time dependency in the process or in its variance, for instance. Then there is the further question as to whether the IBS indicator is mean-reverting, which would indicate that the underlying price process likewise has a tendency to mean revert.
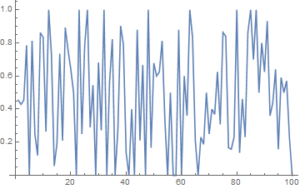
Let’s take the IBS series for Exxon-Mobil (XOM) as an example to work with. I have computed the series from the beginning of 1990, and the first 100 values are shown in the plot below.
Autocorrelation and Unit Root Tests
There appears to be little patterning in the process autocorrelations, and this is confirmed by formal statistical tests which fail to reject the null hypothesis that the first 20 autocorrelations are not, collectively, statistically significant.
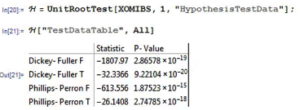
Next we test for the presence of a unit root in the IBS process (highly unlikely, given its construction) and indeed, unsurprisingly, the null hypothesis of a unit root is roundly rejected by the Dickey-Fuller and Phillips-Perron tests.
Variance Ratio Tests
We next conduct a formal test to determine whether the IBS series follows a random walk.
The variance ratio test assesses the null hypothesis that a univariate time series y is a random walk. The null model is
y(t) = c + y(t–1) + e(t),
where c is a drift constant (assumed zero for the IBS series) and e(t) are uncorrelated innovations with zero mean.
- When
IIDisfalse, the alternative is that the e(t) are correlated. - When
IIDistrue, the alternative is that the e(t) are either dependent or not identically distributed (for example, heteroscedastic).
We test whether the XOM IBS series is a random walk using various step sizes and perform the test with and without the assumption that the innovations are independent and identically distributed.
Switching to Matlab, we proceed as follows:
q = [2 4 8 2 4 8];
flag = logical([1 1 1 0 0 0]);
[h,pValue,stat,cValue,ratio] = vratiotest(XOMIBS,’period’,q,’IID’,flag)
Here h is a vector of Boolean decisions for the tests, with length equal to the number of tests. Values of h equal to 1 indicate rejection of the random-walk null in favor of the alternative. Values of h equal to 0 indicate a failure to reject the random-walk null.
The variable ratio is a vector of variance ratios, with length equal to the number of tests. Each ratio is the ratio of:
- The variance of the q-fold overlapping return horizon
- q times the variance of the return series
For a random walk, these ratios are asymptotically equal to one. For a mean-reverting series, the ratios are less than one. For a mean-averting series, the ratios are greater than one.
For the XOM IBS process we obtain the following results:
h = 1 1 1 1 1 1
pValue = 1.0e-51 * [0.0000 0.0000 0.0000 0.0000 0.0000 0.1027]
stat = -27.9267 -21.7401 -15.9374 -25.1412 -20.2611 -15.2808
cValue = 1.9600 1.9600 1.9600 1.9600 1.9600 1.9600
ratio = 0.4787 0.2405 0.1191 0.4787 0.2405 0.1191
The random walk hypothesis is convincingly rejected for both IID and non-IID error terms. The very low ratio values indicate that the IBS process is strongly mean reverting.
Conclusion
While standard statistical tests fail to find evidence of any non-stationarity in the Internal Bar Strength signal for Exxon-Mobil, the hypothesis that the series follows a random walk (with zero drift) is roundly rejected by variance ratio tests. These tests also confirm that the IBS series is strongly mean reverting, as we previously discovered empirically.
This represents an ideal scenario for trading purposes: a signal with the highly desirable properties that is both stationary and mean reverting. In the case of Exxon-Mobil, there appears to be clear evidence from both statistical tests and empirical trading strategies using the Internal Bar Strength indicator that the tendency of the price series to mean-revert is economically as well as statistically significant.


One Reply to “Is Internal Bar Strength A Random Walk? The Case of Exxon-Mobil”
Comments are closed.