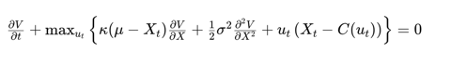Building a winning strategy, like the one in the e-Mini S&P500 futures described here is only half the challenge: it remains for the strategy architect to gain an understanding of the sources of strategy alpha, and risk. This means identifying the factors that drive strategy performance and, ideally, building a model so that their relative importance can be evaluated. A more advanced step is the construction of a meta-model that will predict strategy performance and provided recommendations as to whether the strategy should be traded over the upcoming period.
Strategy Performance – Case Study
Let’s take a look at how this works in practice. Our case study makes use of the following daytrading strategy in e-Mini futures.
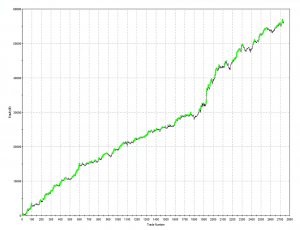
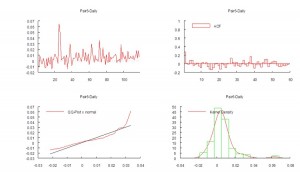
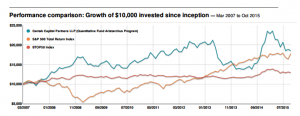
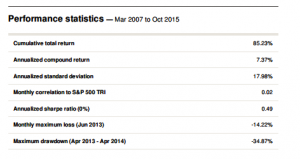
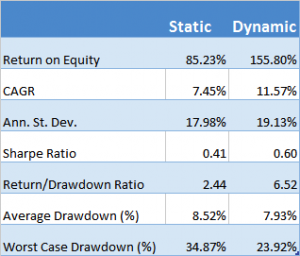
The overall performance of the strategy is quite good. Average monthly PNL over the period from April to Oct 2015 is almost $8,000 per contract, after fees, with a standard deviation of only $5,500. That equates to an annual Sharpe Ratio in the region of 5.0. On a decent execution platform the strategy should scale to around 10-15 contracts, with an annual PNL of around $1.0 to $1.5 million.
Looking into the performance more closely we find that the win rate (56%) and profit factor (1.43) are typical for a profitable strategy of medium frequency, trading around 20 times per session (in this case from 9:30AM to 4PM EST).

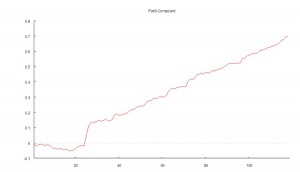
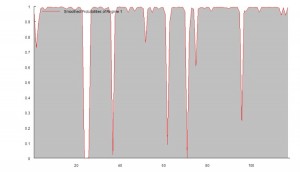
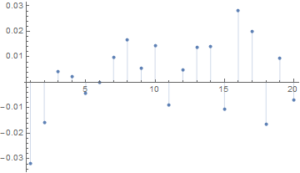
Another attractive feature of the strategy risk profile is the Max Adverse Execution, the drawdown experienced in individual trades (rather than the realized drawdown). In the chart below we see that the MAE increases steadily, without major outliers, to a maximum of only around $1,000 per contract.
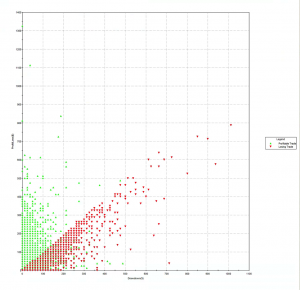
One concern is that the average trade PL is rather small – $20, just over 1.5 ticks. Strategies that enter and exit with limit orders and have small average trade are generally highly dependent on the fill rate – i.e. the proportion of limit orders that are filled. If the fill rate is too low, the strategy will be left with too many missed trades on entry or exit, or both. This is likely to damage strategy performance, perhaps to a significant degree – see, for example my post on High Frequency Trading Strategies.
The fill rate is dependent on the number of limit orders posted at the extreme high or low of the bar, known as the extreme hit rate. In this case the strategy has been designed specifically to operate at an extreme hit rate of only around 10%, which means that, on average, only around one trade in ten occurs at the high or low of the bar. Consequently, the strategy is not highly fill-rate dependent and should execute satisfactorily even on a retail platform like Tradestation or Interactive Brokers.
Drivers of Strategy Performance
So far so good. But before we put the strategy into production, let’s try to understand some of the key factors that determine its performance. Hopefully that way we will be better placed to judge how profitable the strategy is likely to be as market conditions evolve.
In fact, we have already identified one potential key performance driver: the extreme hit rate (required fill rate) and determined that it is not a major concern in this case. However, in cases where the extreme hit rate rises to perhaps 20%, or more, the fill ratio is likely to become a major factor in determining the success of the strategy. It would be highly inadvisable to attempt implementation of such a strategy on a retail platform.

What other factors might affect strategy performance? The correct approach here is to apply the scientific method: develop some theories about the drivers of performance and see if we can find evidence to support them.
For this case study we might conjecture that, since the strategy enters and exits using limit orders, it should exhibit characteristics of a mean reversion strategy, which will tend to do better when the market moves sideways and rather worse in a strongly trending market.
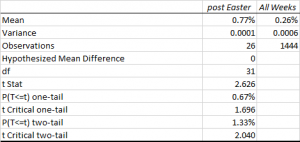
Another hypothesis is that, in common with most day-trading and high frequency strategies, this strategy will produce better results during periods of higher market volatility. Empirically, HFT firms have always produced higher profits during volatile market conditions – 2008 was a banner year for many of them, for example. In broad terms, times when the market is whipsawing around create additional opportunities for strategies that seek to exploit temporary mis-pricings. We shall attempt to qualify this general understanding shortly. For now let’s try to gather some evidence that might support the hypotheses we have formulated.
I am going to take a very simple approach to this, using linear regression analysis. It’s possible to do much more sophisticated analysis using nonlinear methods, including machine learning techniques. In our regression model the dependent variable will be the daily strategy returns. In the first iteration, let’s use measures of market returns, trading volume and market volatility as the independent variables.
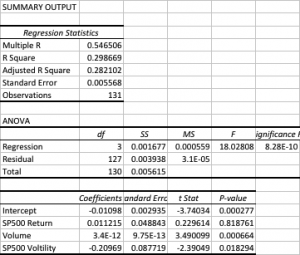
The first surprise is the size of the (adjusted) R Square – at 28%, this far exceeds the typical 5% to 10% level achieved in most such regression models, when applied to trading systems. In other words, this model does a very good job of account for a large proportion of the variation in strategy returns.
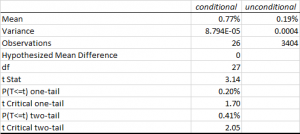
Note that the returns in the underlying S&P50o index play no part (the coefficient is not statistically significant). We might expect this: ours is is a trading strategy that is not specifically designed to be directional and has approximately equivalent performance characteristics on both the long and short side, as you can see from the performance report.
Now for the next surprise: the sign of the volatility coefficient. Our ex-ante hypothesis is that the strategy would benefit from higher levels of market volatility. In fact, the reverse appears to be true (due to the negative coefficient). How can this be? On further reflection, the reason why most HFT strategies tend to benefit from higher market volatility is that they are momentum strategies. A momentum strategy typically enters and exits using market orders and hence requires a major market move to overcome the drag of the bid-offer spread (assuming it calls the market direction correctly!). This strategy, by contrast, is a mean-reversion strategy, since entry/exits are effected using limit orders. The strategy wants the S&P500 index to revert to the mean – a large move that continues in the same direction is going to hurt, not help, this strategy.
Note, by contrast, that the coefficient for the volume factor is positive and statistically significant. Again this makes sense: as anyone who has traded the e-mini futures overnight can tell you, the market tends to make major moves when volume is light – simply because it is easier to push around. Conversely, during a heavy trading day there is likely to be significant opposition to a move in any direction. In other words, the market is more likely to trade sideways on days when trading volume is high, and this is beneficial for our strategy.
The final surprise and perhaps the greatest of all, is that the strategy alpha appears to be negative (and statistically significant)! How can this be? What the regression analysis appears to be telling us is that the strategy’s performance is largely determined by two underlying factors, volume and volatility.
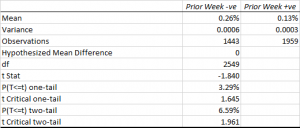
Let’s dig into this a little more deeply with another regression, this time relating the current day’s strategy return to the prior day’s volume, volatility and market return.
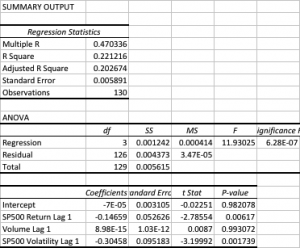
In this regression model the strategy alpha is effectively zero and statistically insignificant, as is the case for lagged volume. The strategy returns relate inversely to the prior day’s market return, which again appears to make sense for a mean reversion strategy: our model anticipates that, in the mean, the market will reverse the prior day’s gain or loss. The coefficient for the lagged volatility factor is once again negative and statistically significant. This, too, makes sense: volatility tends to be highly autocorrelated, so if the strategy performance is dependent on market volatility during the current session, it is likely to show dependency on volatility in the prior day’s session also.
So, in summary, we can provisionally conclude that:
This strategy has no market directional predictive power: rather it is a pure, mean-reversal strategy that looks to make money by betting on a reversal in the prior session’s market direction. It will do better during periods when trading volume is high, and when market volatility is low.
Conclusion
Now that we have some understanding of where the strategy performance comes from, where do we go from here? The next steps might include some, or all, of the following:
(i) A more sophisticated econometric model bringing in additional lags of the explanatory variables and allowing for interaction effects between them.
(ii) Introducing additional exogenous variables that may have predictive power. Depending on the nature of the strategy, likely candidates might include related equity indices and futures contracts.
(iii) Constructing a predictive model and meta-strategy that would enable us assess the likely future performance of the strategy, and which could then be used to determine position size. Machine learning techniques can often be helpful in this content.
I will give an example of the latter approach in my next post.