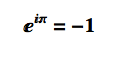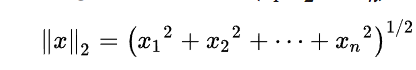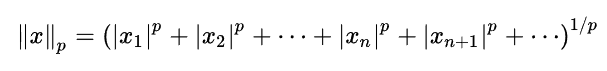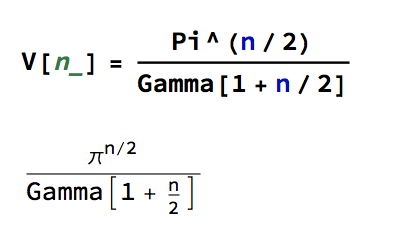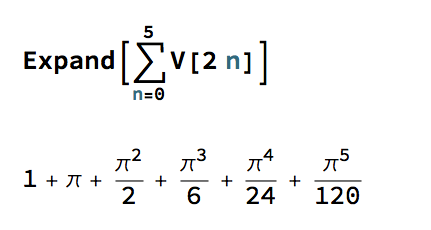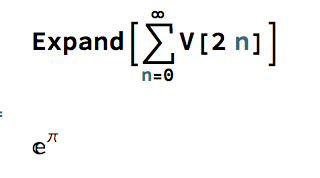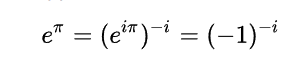One of the most beautiful equations in the whole of mathematics is the identity (and its derivation):
I recently came across another beautiful mathematical concept that likewise relates the two transcendental numbers e and Pi.
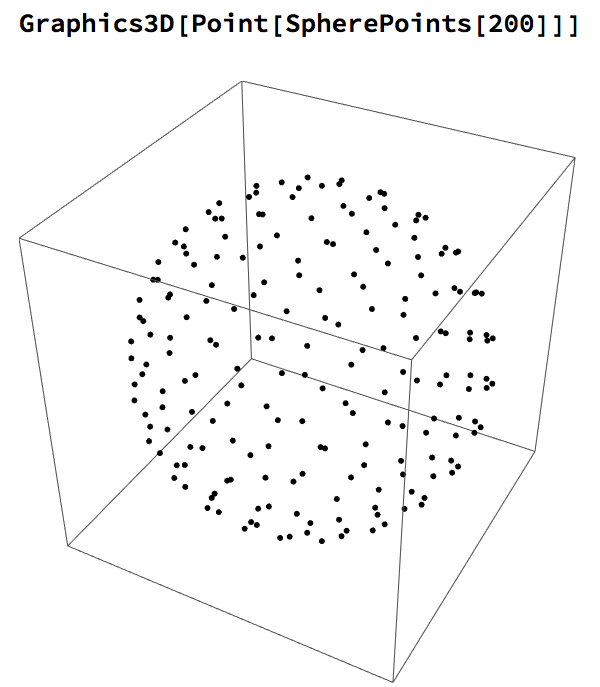
We begin by reviewing the concept of a unit sphere, which in 3-dimensional space is the region of points described by the equation:
We can some generate random coordinates that satisfy the equation, to produce the expected result:
The equation above represents a 3-D unit sphere using the standard Euclidean Norm. It can be generalized to produce a similar formula for an n-dimensional hyper-sphere:
Another way to generalize the concept is by extending the Euclidean distance measure with what are referred to as p-Norms, or L-p spaces:
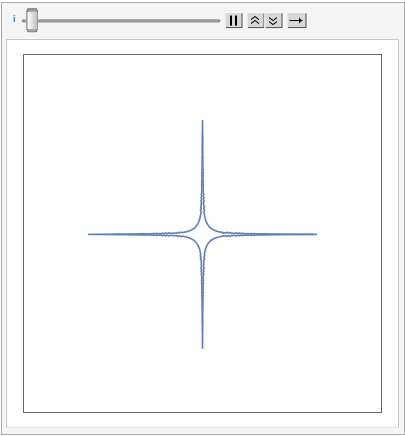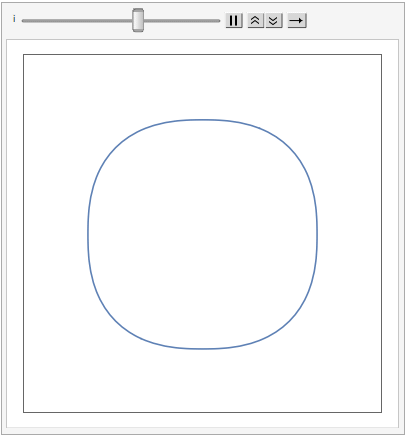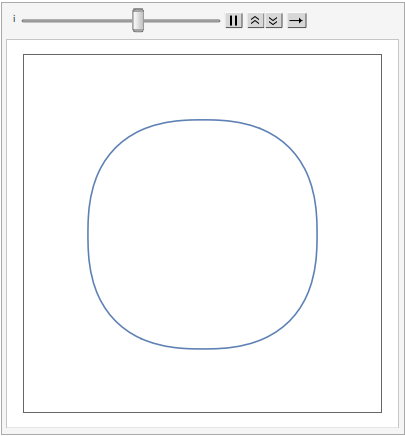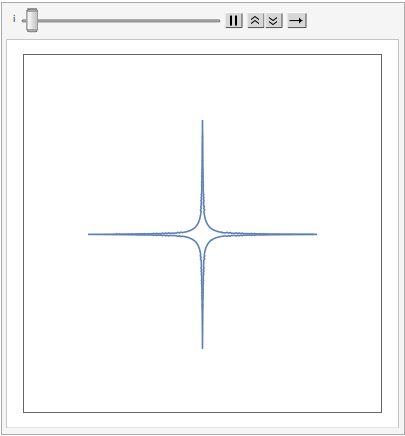
The shape of a unit sphere in L-p space can take many different forms, including some that have “corners”. Here are some examples of 2-dimensional spheres for values of p varying in the range { 0.25, 4}:
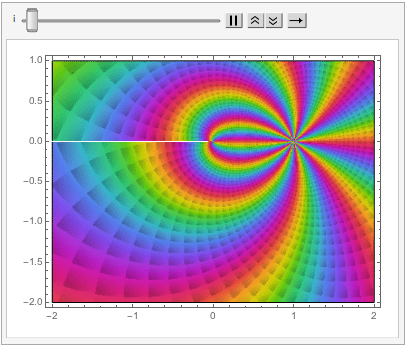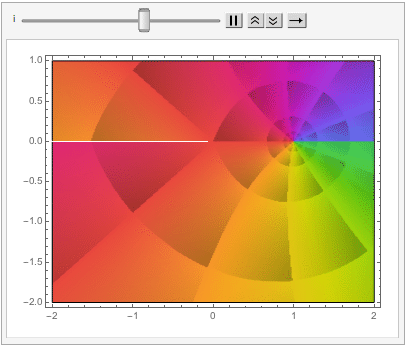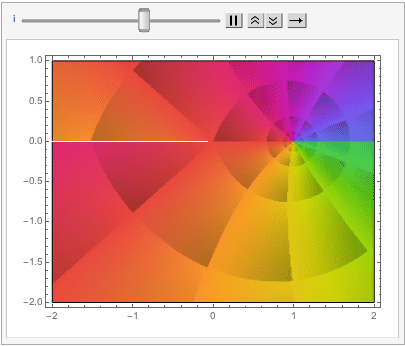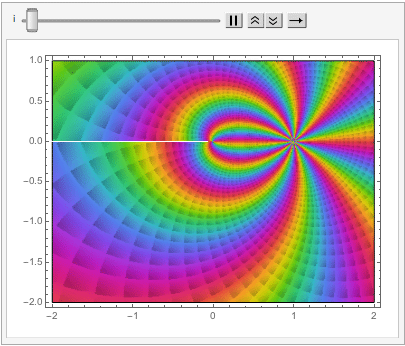
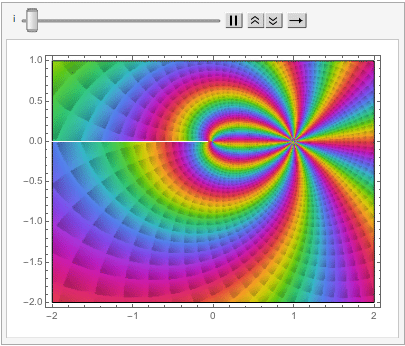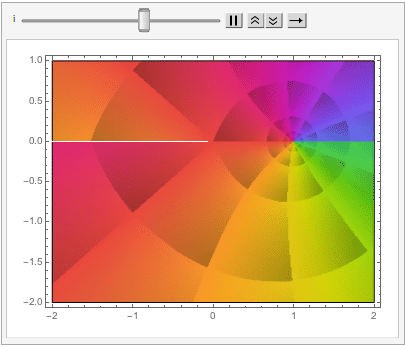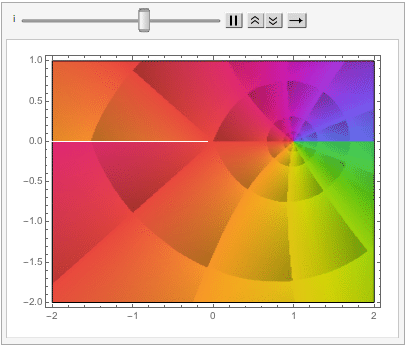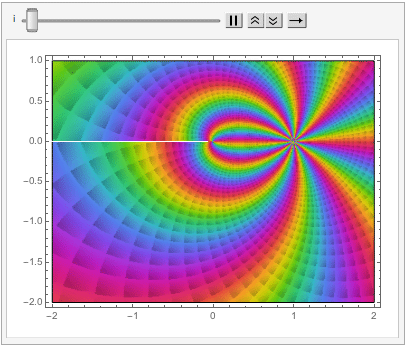
which can also be explored in the complex plane:
Reverting to the regular Euclidean metric, let’s focus on the n-dimensional unit hypersphere, whose volume is given by:
To see this, note that the volume of the unit sphere in 2-D space is just the surface area of a unit circle, which has area V(2) = π. Furthermore:
This is the equation for the volume of the unit hypersphere in n dimensions. Hence we have the following recurrence relationship:
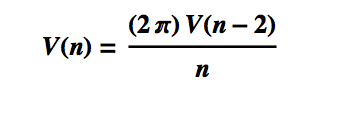This recursion allows us to prove the equation for the volume of the unit hypersphere, by induction.
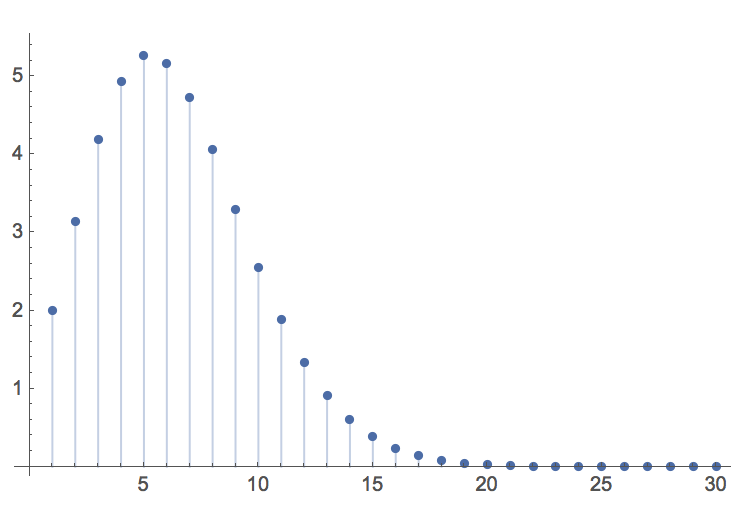
The function V(n) take a maximal value of 5.26 for n = 5 dimensions, thereafter declining rapidly towards zero:
In the limit, the volume of the n-dimensional unit hypersphere tends to zero:
Now, consider the sum of the volumes of unit hypersphere in even dimensions, i.e. for n = 0, 2, 4, 6,…. For example, the first few terms of the sum are:
These are the initial terms of a well-known McClaurin expansion, which in the limit produces the following remarkable result:
In other words, the infinite sum of the volumes of n-dimensional unit hyperspheres evaluates to a power relationship between the two most famous transcendental numbers. The result, known as Gelfond’s constant, is itself a transcendental number:
