In the previous post I outlined some of the available techniques used for modeling market states. The following is an illustration of how these techniques can be applied in practice. You can download this post in pdf format here.
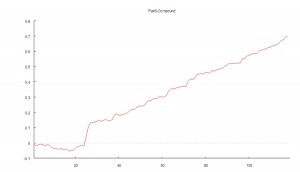
The chart below shows the daily compounded returns for a single pair in an ETF statistical arbitrage strategy, back-tested over a 1-year period from April 2010 to March 2011.
The idea is to examine the characteristics of the returns process and assess its predictability.
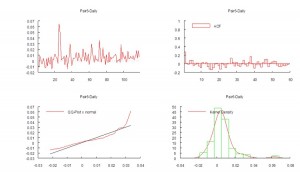
The initial impression given by the analytics plots of daily returns, shown in Fig 2 below, is that the process may be somewhat predictable, given what appears to be a significant 1-order lag in the autocorrelation spectrum. We also see evidence of the
customary non-Gaussian “fat-tailed” distribution in the error process.
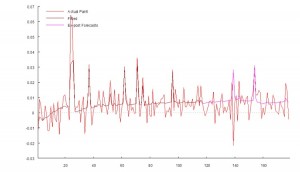
An initial attempt to fit a standard Auto-Regressive Moving Average ARMA(1,0,1) model yields disappointing results, with an unadjusted model R-squared of only 7% (see model output in Appendix 1)
However, by fitting a 2-state Markov model we are able to explain as much as 65% in the variation in the returns process (see Appendix II).
The model estimates Markov Transition Probabilities as follows.
P(.|1) P(.|2)
P(1|.) 0.93920 0.69781
P(2|.) 0.060802 0.30219
In other words, the process spends most of the time in State 1, switching to State 2 around once a month, as illustrated in Fig 3 below.
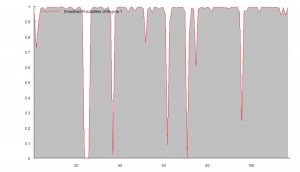
In the first state, the pairs model produces an expected daily return of around 65bp, with a standard deviation of similar magnitude. In this state, the process also exhibits very significant auto-regressive and moving average features.
Regime 1:
Intercept 0.00648 0.0009 7.2 0
AR1 0.92569 0.01897 48.797 0
MA1 -0.96264 0.02111 -45.601 0
Error Variance^(1/2) 0.00666 0.0007
In the second state, the pairs model produces lower average returns, and with much greater variability, while the autoregressive and moving average terms are poorly determined.
Regime 2:
Intercept 0.03554 0.04778 0.744 0.459
AR1 0.79349 0.06418 12.364 0
MA1 -0.76904 0.51601 -1.49 0.139
Error Variance^(1/2) 0.01819 0.0031
CONCLUSION
The analysis in Appendix II suggests that the residual process is stable and Gaussian. In other words, the two-state Markov model is able to account for the non-Normality of the returns process and extract the salient autoregressive and moving average features in a way that makes economic sense.
How is this information useful? Potentially in two ways:
(i) If the market state can be forecast successfully, we can use that information to increase our capital allocation during periods when the process is predicted to be in State 1, and reduce the allocation at times when it is in State 2.
(ii) By examining the timing of the Markov states and considering different features of the market during the contrasting periods, we might be able to identify additional explanatory factors that could be used to further enhance the trading model.