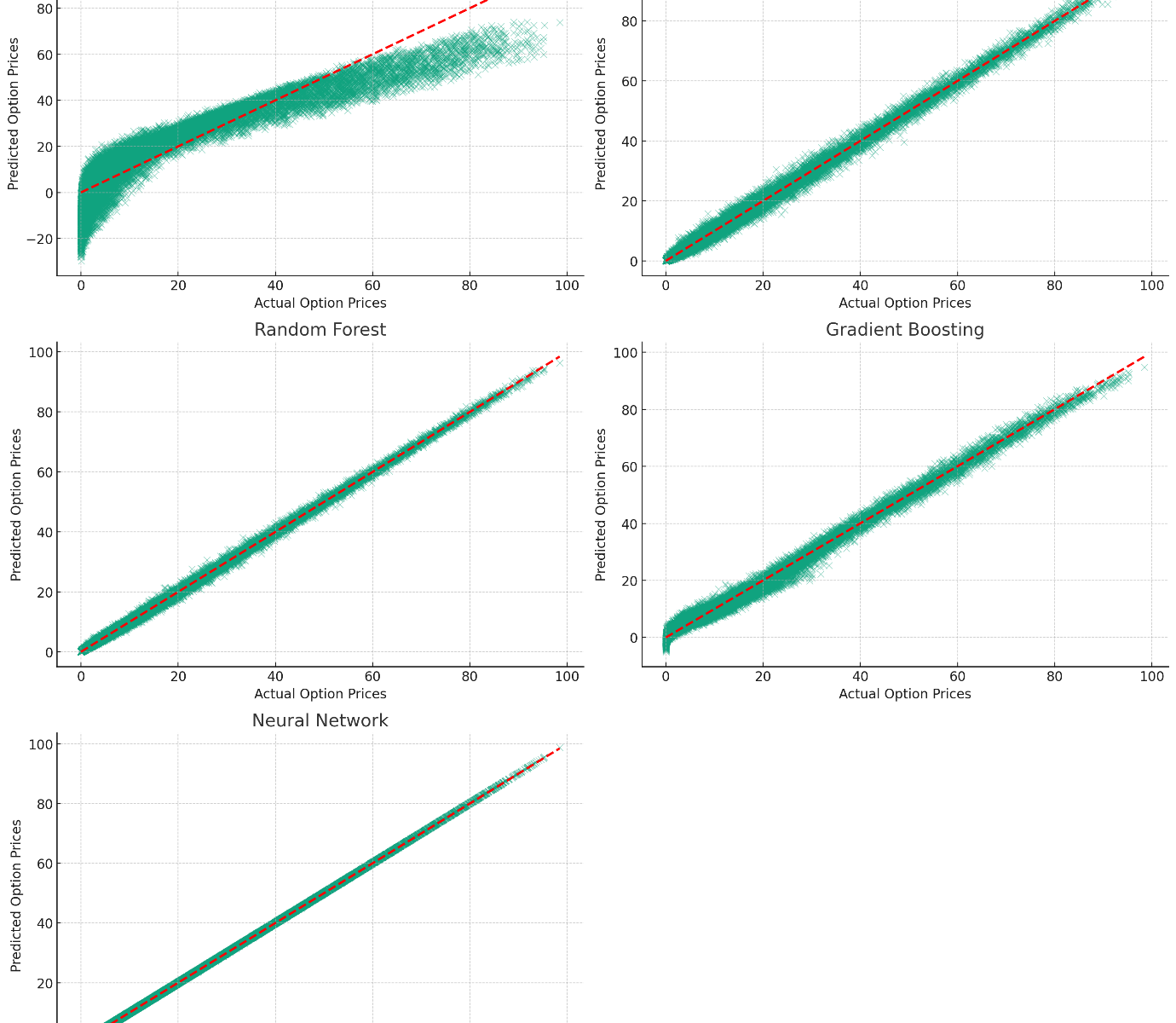
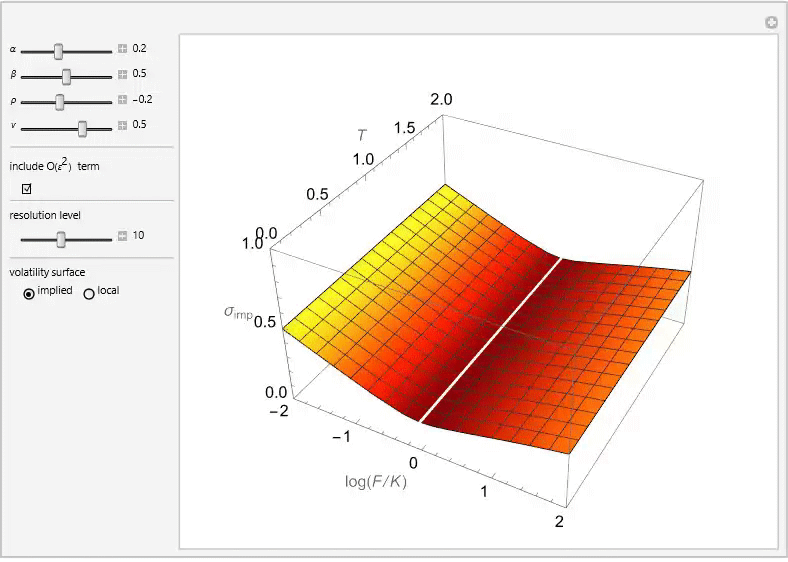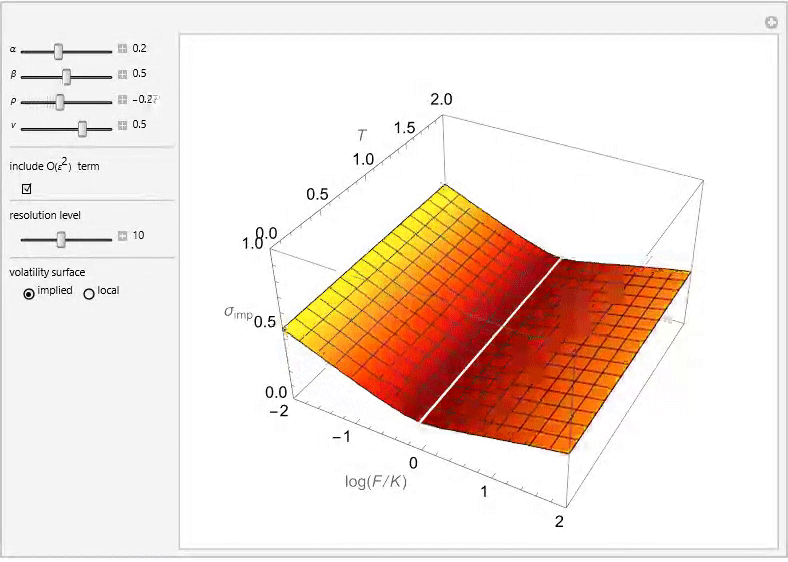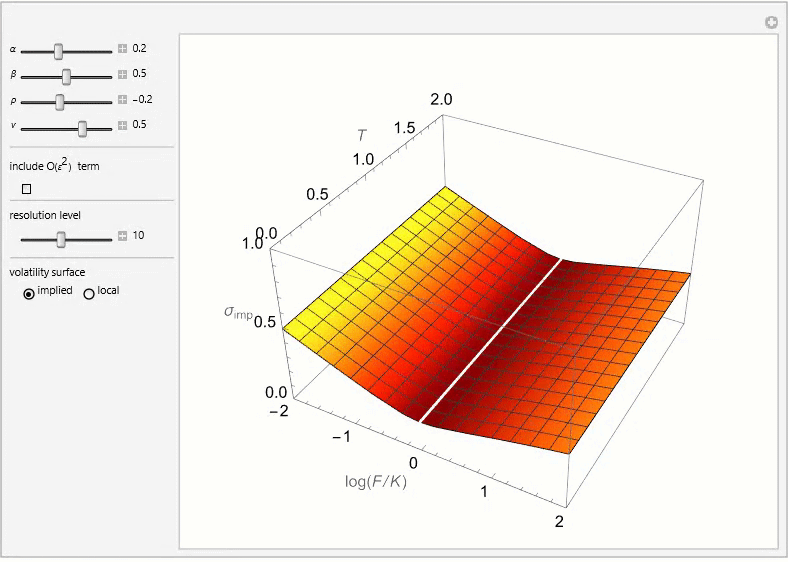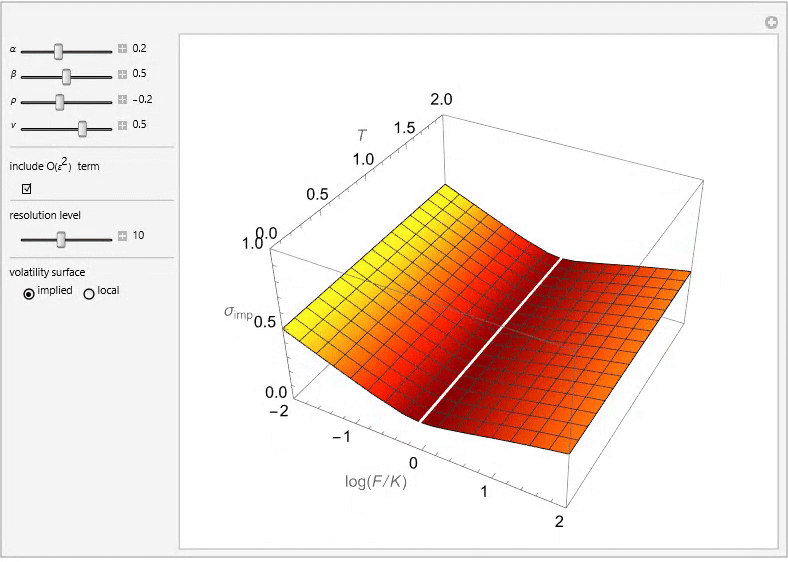
The SABR Stochastic Volatility Model
The SABR (Stochastic Alpha, Beta, Rho) model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for “Stochastic Alpha, Beta, Rho”, referring to the parameters of the model. The model was developed by Patrick Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward.
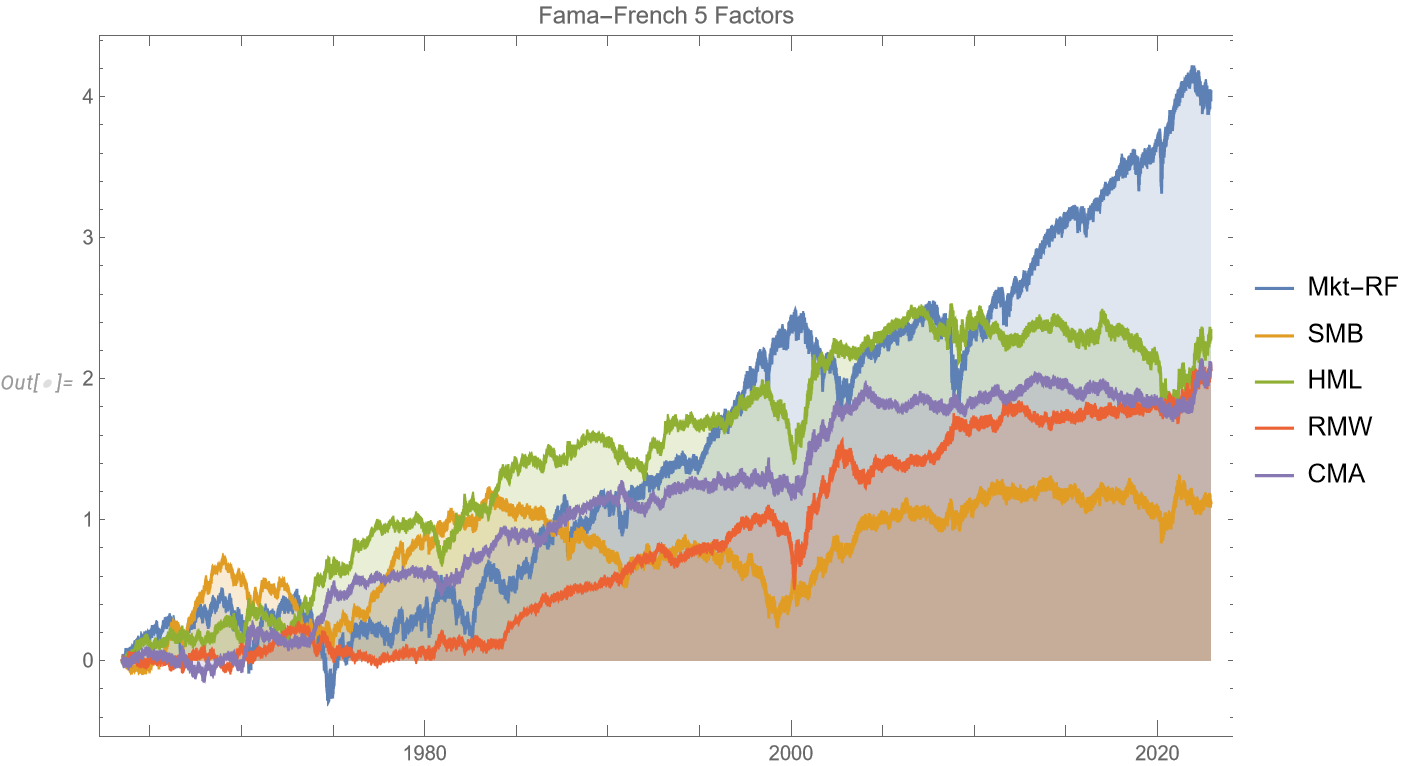
Seasonality in Equity Returns
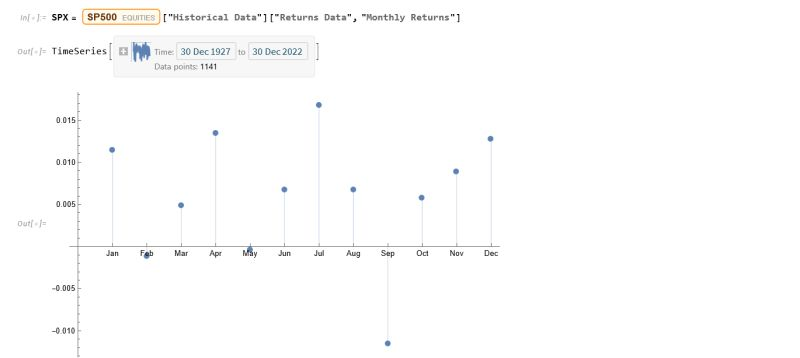
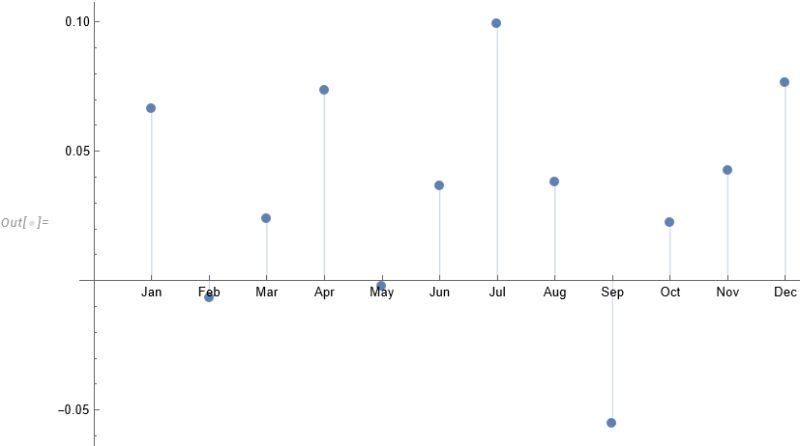
To amplify Valérie Noël‘s post a little, we can use the Equities Entity Store (https://lnkd.in/epg-5wwM) to extract returns for the S&P500 index for (almost) the last century and compute the average return by month, as follows.
July is shown to be (by far) the most positive month for the index, with an average return of +1.67%, in stark contrast to the month of Sept. in which the index has experienced an average negative return of -1.15%.
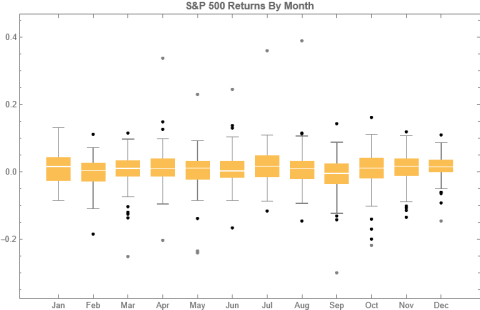
Continuing the analysis a little further, we can again use the the Equities Entity Store (https://lnkd.in/epg-5wwM) to extract estimated average volatility for the S&P500 by calendar month since 1927:
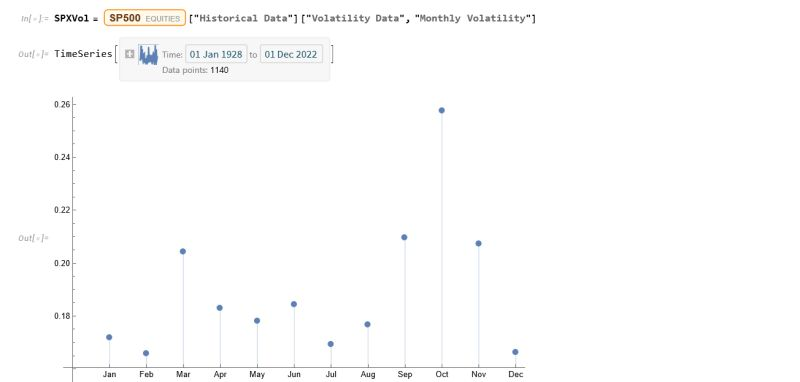
As you can see, July is not only the month with highest average monthly return, but also has amongst the lowest levels of volatility, on average.
Consequently, risk-adjusted average rates of return in July far exceed other months of the year.
Conclusion: bears certainly have a case that the market is over-stretched here, but I would urge caution: hold off until end Q3 before shorting this market in significant size.
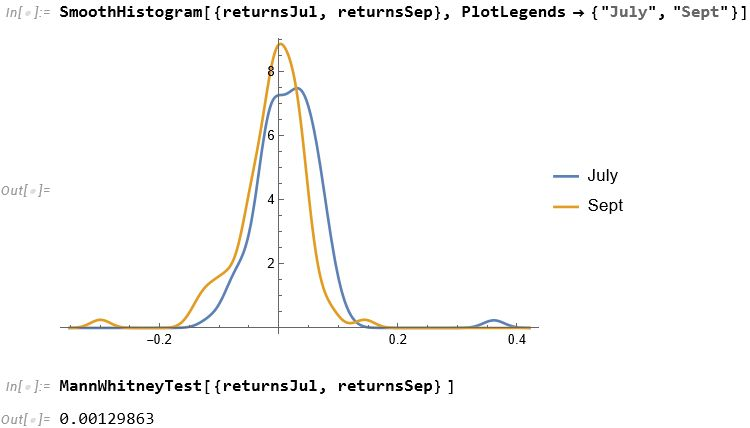
For those market analysts who prefer a little more analytical meat, we can compare the median returns for the #S&P500 Index for the months of July and September using the nonparametric MannWhitney test.
This indicates that there is only a 0.13% probability that the series of returns for the two months are generated from distributions with the same median.
Conclusion: Index performance in July really is much better than in September.
For more analysis along these lines, see my recent book, Equity Analytics:

Najboljši Spletni Casinoji: Vaš Vodnik do Vrhunskih Igralnih Izkušenj
V današnjem digitalnem svetu se spletni casinoji hitro uveljavljajo kot priljubljena destinacija za ljubitelje igralništva. Z raznoliko ponudbo iger, atraktivnimi bonusi in udobnostjo igranja od doma so spletni casinoji postali nepogrešljiv del igralniške kulture. V tem vodniku bomo pregledali najboljši spletni casinoji, ki vam ponujajo vrhunsko igralno izkušnjo in možnosti za velike dobitke.

1. JackpotCity Casino
JackpotCity Casino je eden najbolj priljubljenih spletnih casinojev med igralci po vsem svetu, vključno s Slovenijo. Z bogato ponudbo več kot 500 iger, vključno s številnimi različnimi različicami iger, kot so igralni avtomati, ruleta, blackjack in poker, JackpotCity zagotavlja nekaj za vsakogar. Poleg tega ponuja tudi atraktivne bonuse za nove igralce in zvestobo, kar povečuje vaše možnosti za zmago.
2. Betway Casino
Betway Casino je znan po svoji visoki kakovosti storitev in impresivni izbiri iger. Spletne reže, mize za blackjack in ruleto, ter vrhunski poker vam ponujajo vrhunsko izkušnjo igranja. Poleg tega Betway ponuja tudi številne promocije in bonuse, vključno z dobrodošlim bonusom za nove igralce, ki vam pomaga začeti vašo igralno pot s pravo nogo.
3. 888 Casino
888 Casino je eden najstarejših in najbolj spoštovanih spletnih casinojev v industriji. S svojo izjemno izbiro iger, visoko kakovostno grafiko in zvokom ter zanesljivim delovanjem platforme ponuja izjemno igralno izkušnjo. Poleg tega 888 Casino ponuja tudi velikodušne bonuse, vključno z dobrodošlim paketom za nove igralce in rednimi promocijami za obstoječe igralce.
4. LeoVegas Casino
LeoVegas Casino se ponaša z nazivom “Kralj mobilnega igralništva” in to z dobrim razlogom. Njihova mobilna aplikacija je ena najboljših v industriji, kar vam omogoča igranje vaših najljubših iger kjerkoli in kadarkoli. Poleg tega LeoVegas ponuja tudi široko paleto iger, visoke bonuse in hitre izplačila, kar ga postavlja med vodilne igralnice na trgu.
5. Bitstarz Casino
Bitstarz Casino je specializiran za bitcoin in druge kriptovalute, kar ga naredi privlačno izbiro za tiste, ki želijo igrati s kripto valutami. S široko paleto iger, hitrimi izplačili in zanesljivo platformo je Bitstarz postal priljubljena destinacija med igralci po vsem svetu.
Kako Izbrati Najboljši Spletni Casino za Vas
Pri izbiri najboljšega spletnega casinoja je pomembno upoštevati več dejavnikov, ki vplivajo na vašo izkušnjo igranja. Tu je nekaj ključnih stvari, na katere morate biti pozorni:
- Izbor Iger: Preverite, ali spletni casino ponuja široko paleto iger, ki ustrezajo vašim željam in preferencam.
- Boniteti in Promocije: Bodite pozorni na bonitete za nove igralce, kot tudi na redne promocije in nagrade za zvestobo.
- Varstvo Potrošnikov: Preverite, ali ima spletni casino ustrezne licence in certifikate ter ali uporablja varne metode plačevanja in šifriranje podatkov.
- Mobilna Združljivost: Če radi igrate na poti, preverite, ali ima spletni casino ustrezen mobilni vmesnik ali aplikacijo.
- Podpora za Stranke: Preverite, ali spletni casino ponuja učinkovito podporo strankam, ki vam bo pomagala pri morebitnih težavah ali vprašanjih.
Z upoštevanjem teh dejavnikov boste lahko izbrali najboljši spletni casino, ki bo ustrezal vašim potrebam in pričakovanjem. Srečno igranje!
Unveiling the Panaloko Casino Online: A Comprehensive Review by CasinoPhilippines10
In the vibrant world of online casinos, Filipino players are constantly seeking new and exciting platforms to satisfy their gaming needs. Among the plethora of options available, Panaloko Casino Online emerges as a prominent contender, offering a diverse range of games, enticing bonuses, and a secure gaming environment. In this comprehensive review, we delve into the features, games, bonuses, security measures, and overall experience offered by Panaloko Casino Online, as assessed by CasinoPhilippines10.

Understanding Panaloko Casino Online
Introduction to Panaloko Casino Online: Panaloko Casino Online is a dynamic online gaming platform that caters to players in the Philippines and beyond. Renowned for its extensive selection of games, generous bonuses, and user-friendly interface, Panaloko Casino Online has garnered a loyal following among players seeking an immersive and rewarding gaming experience.
CasinoPhilippines10: Your Trusted Review Site: CasinoPhilippines10 stands as a trusted authority in the world of online casino reviews, providing impartial and comprehensive assessments to assist players in making informed decisions. With a commitment to transparency and integrity, CasinoPhilippines10 evaluates Panaloko Casino Online based on a variety of criteria, including game variety, bonuses, security measures, and customer support.
Features of Panaloko Casino Online
Rich Gaming Selection: Panaloko Casino Online boasts a diverse gaming library featuring a wide range of options to suit every player’s preferences. From classic slots and table games to live dealer experiences, there’s something for everyone to enjoy at Panaloko Casino Online.
User-Friendly Interface: Navigating the platform is intuitive and seamless, thanks to its user-friendly interface. Players can easily access their favorite games, explore promotional offers, and manage their accounts with ease, enhancing the overall gaming experience.
Mobile Compatibility: For players who prefer gaming on the go, Panaloko Casino Online offers seamless mobile compatibility. Whether on a smartphone or tablet, players can enjoy their favorite games anytime, anywhere, without compromising on quality or performance.
Secure Payment Options: The casino provides a range of secure payment options to facilitate deposits and withdrawals, ensuring that players’ financial transactions are conducted safely and efficiently.
Generous Bonuses and Promotions: Players are greeted with a plethora of bonuses and promotions upon signing up at Panaloko Casino Online. From welcome bonuses to reload offers and loyalty rewards, there are ample opportunities for players to boost their bankrolls and enhance their gaming experience.
Customer Support: A dedicated customer support team is available to assist players with any queries or concerns they may have. Whether via live chat, email, or phone, responsive customer support enhances the overall gaming experience.
Games Offered at Panaloko Casino Online
Slots: Dive into a world of excitement with a diverse selection of slot games, ranging from classic fruit machines to cutting-edge video slots featuring immersive graphics and engaging gameplay mechanics.
Table Games: For fans of traditional casino games, Panaloko Casino Online offers a variety of table games, including blackjack, roulette, baccarat, and poker variants. With realistic graphics and intuitive controls, players can enjoy the thrill of the casino floor from the comfort of their homes.
Live Dealer Experiences: Immerse yourself in the ultimate gaming experience with live dealer games. Interact with professional dealers in real-time as you play classic casino games such as blackjack, roulette, and baccarat, bringing the excitement of the casino directly to your screen.
Bonuses and Promotions at Panaloko Casino Online
Welcome Bonus: New players are welcomed with open arms at Panaloko Casino Online, greeted by a generous welcome bonus package that often includes a combination of deposit matches, free spins, and other incentives to kickstart their gaming journey.
Reload Bonuses: Returning players can take advantage of reload bonuses offered by Panaloko Casino Online. These bonuses typically reward players with additional funds or free spins when they make subsequent deposits into their accounts.
Loyalty Program: Panaloko Casino Online rewards loyal players through its loyalty program, allowing them to earn points for every wager placed. These points can be exchanged for various rewards, including cashback, exclusive bonuses, and access to VIP perks.
Security Measures at Panaloko Casino Online
Player safety is a top priority at Panaloko Casino Online, with robust security measures in place to protect sensitive information. The casino employs advanced encryption technology to safeguard financial transactions and personal data, providing players with peace of mind while they enjoy their gaming experience.
Regulatory Compliance
Panaloko Casino Online operates under a valid license issued by a reputable gaming authority, ensuring compliance with industry standards and regulatory requirements. Players can trust that the casino adheres to strict guidelines regarding fair gaming practices and responsible gambling initiatives.
Customer Support
A dedicated team of support agents is available to assist players with any inquiries or issues they may encounter. Whether it’s assistance with account-related matters, questions about bonuses, or technical support, players can rely on the responsive customer support team at Panaloko Casino Online to provide prompt and courteous assistance.
Conclusion
In conclusion, Panaloko Casino Online offers a compelling gaming experience for players in the Philippines, with its diverse selection of games, generous bonuses, secure gameplay, and responsive customer support. Whether you’re a seasoned gambler or new to the world of online casinos, Panaloko Casino Online provides a welcoming and enjoyable environment to satisfy your gaming needs. Join Panaloko Casino Online today and embark on an exciting journey filled with entertainment and rewards.
KasynoOnline10: Profesjonalny Portal Recenzujący Kasyna Online dla Polaków w Holandii
Rynek hazardu online stale się rozwija, a gracze poszukują wiarygodnych źródeł informacji, które pomogą im dokonać najlepszych wyborów w świecie kasyn internetowych. Dla Polaków mieszkających w Holandii, dostęp do odpowiednich recenzji kasyn online może być kluczowy. W tym artykule przyjrzymy się KasynoOnline10, renomowanemu portalowi recenzującemu, który oferuje bogactwo informacji dla polskojęzycznych graczy w Holandii: https://kasynoonline10.com.

Historia i Renoma
KasynoOnline10 to znany i szanowany portal recenzujący, który istnieje na rynku od wielu lat. Dzięki swojej długiej historii i profesjonalizmowi zdobył zaufanie wielu graczy, zarówno w Polsce, jak i za granicą. Jego recenzje są cenione za szczegółowość i obiektywizm, co sprawia, że jest to niezastąpione źródło informacji dla osób poszukujących wiarygodnych opinii na temat kasyn online.
Zakres Recenzji
KasynoOnline10 oferuje szeroki zakres recenzji, który obejmuje różnorodne aspekty kasyn online. Od popularnych gier kasynowych, takich jak sloty, ruletka czy blackjack, po zakłady bukmacherskie i pokera online – każdy znajdzie tutaj informacje odpowiadające jego zainteresowaniom. Szczególnie dla Polaków w Holandii, którzy mogą mieć ograniczony dostęp do polskojęzycznych źródeł informacji, KasynoOnline10 stanowi cenny zasób w ich poszukiwaniach.
Bezpieczeństwo i Licencje
Bezpieczeństwo graczy jest priorytetem KasynoOnline10. Portal ten dokładnie sprawdza licencje i regulacje każdego recenzowanego kasyna, aby zapewnić, że są one zgodne z obowiązującymi przepisami. Dzięki temu gracze mogą mieć pewność, że ich dane osobowe oraz środki finansowe są chronione zgodnie z najwyższymi standardami bezpieczeństwa.
Bonusy i Promocje
KasynoOnline10 szczegółowo analizuje oferty bonusowe i promocje dostępne w kasynach online. Dla Polaków w Holandii, którzy mogą mieć ograniczony dostęp do polskojęzycznych kasyn online, informacje o bonusach powitalnych, darmowych spinach czy programach lojalnościowych mogą być szczególnie cenne. KasynoOnline10 prezentuje warunki bonusów w sposób przejrzysty i zrozumiały, co pozwala graczom świadomie korzystać z ofert promocyjnych.
Obsługa Klienta
Profesjonalna obsługa klienta jest kluczowym elementem każdego kasyna online. KasynoOnline10 sprawdza, jak szybko i sprawnie reagują na zapytania i problemy graczy recenzowane kasyna. Oceniana jest dostępność różnych kanałów komunikacji oraz jakość obsługi klienta, co daje graczom pewność, że w przypadku jakichkolwiek trudności mogą liczyć na wsparcie.
Dostępność na Różnych Platformach
W dobie rosnącej popularności urządzeń mobilnych, KasynoOnline10 bierze pod uwagę dostępność recenzowanych kasyn na różnych platformach. Analiza obejmuje zarówno kasyna dostępne na komputerach stacjonarnych, jak i na smartfonach czy tabletach. Dzięki temu gracze mogą cieszyć się ulubionymi grami w dowolnym miejscu i czasie, korzystając z różnych urządzeń.
Podsumowanie
KasynoOnline10 to profesjonalny portal recenzujący, który oferuje bogactwo informacji dla polskojęzycznych graczy w Holandii. Dzięki jego usługom, Polacy mieszkający za granicą mogą nadal cieszyć się grą w kasynach online, mając pewność, że korzystają z renomowanego i godnego zaufania źródła informacji. Bezpieczeństwo, atrakcyjne bonusy, profesjonalna obsługa klienta i szeroki zakres recenzji to tylko niektóre z zalet, jakie oferuje KasynoOnline10. Dla Polaków w Holandii, poszukujących najlepszych kasyn online, KasynoOnline10 stanowi niezastąpione wsparcie i przewodnik po świecie hazardu internetowego.
Заглавие: Онлайн Казино БГ: Изследване на Хазартните Възможности за Български Играчи
Онлайн казино индустрията в България преживява бърз разцвет, предлагайки на играчите вълнуващи възможности за хазартни забавления и печалби от уюта на техния дом. В този материал ще проучим какво представлява онлайн казино БГ, как работят тези платформи и как българските играчи могат да се възползват от тях.

1. Какво представлява Онлайн Казино БГ:
- Разнообразие от Сайтове: Онлайн казино БГ включва разнообразие от сайтове, които предлагат хазартни игри като слотове, рулетка, блекджек, покер и други.
- Лицензиране и Регулация: Мнозинството от тези сайтове са лицензирани и регулирани от Българската Комисия по Хазарта, което гарантира честност и сигурност за играчите.
2. Как Работят Онлайн Казината в България:
- Софтуерни Платформи: Онлайн казината използват специализирани софтуерни платформи, които осигуряват честни игри и сигурни финансови транзакции.
- Различни Методи за Плащане: Играчите могат да използват различни методи за плащане като кредитни карти, електронни портфейли и банкови трансфери за финансиране на своите сметки.
3. Предимства на Онлайн Казино БГ:
- Удобство и Достъпност: Онлайн казината предоставят удобство и достъпност, като играчите могат да играят от всяко място и по всяко време чрез компютър, смартфон или таблет.
- Бонуси и Промоции: Много от онлайн казината предлагат различни бонуси и промоции за нови и редовни играчи, които увеличават шансовете за печалба и забавление.
4. Регулация и Сигурност:
- Защита на Информацията: Онлайн казината в България се грижат за защитата на личната и финансовата информация на своите играчи, използвайки сигурни технологии за шифроване на данните.
- Отговорно Играене: Те също така подкрепят отговорно играене, като предоставят инструменти и ресурси за контрол на хазартното поведение.
5. Бъдещето на Онлайн Казино БГ:
- Технологични Иновации: С развитието на технологиите, очакваме да видим по-иновативни и интерактивни онлайн казино преживявания, включително виртуална реалност и разширена реалност.
- Повече Регулация и Легализация: По-голямото регулиране и легализация на онлайн хазарта в България може да доведе до по-голяма сигурност и доверие в индустрията.
Заключение:
Онлайн казино БГ представлява една от най-популярните форми на забавление за хазартните любители в България. С разнообразието от игри, бонуси и сигурността, която предлагат, те продължават да привличат все по-голям брой играчи. С развитието на технологиите и регулациите, очакваме да видим още по-иновативни и регулирани онлайн казино преживявания в бъдеще.
Najbardziej Wypłacane Kasyno Online: Przegląd KasynoPolska10
W dzisiejszych czasach coraz więcej graczy wybiera rozrywkę w kasynach online, poszukując nie tylko emocji związanych z grą, ale także możliwości wygrania sporych sum pieniędzy. Jednak z powodu dużej liczby dostępnych platform wybór odpowiedniego kasyna online może być trudny. Dlatego też przygotowałem ten przegląd, aby przedstawić czytelnikom KasynoPolska10 najlepsze opcje, jeśli chodzi o najbardziej wypłacane kasyna online: https://pl.kasynopolska10.com/najlepiej-wyplacalne.

Ranking KasynoPolska10: Najlepsze Kasyna Online
1. Vulkan Vegas
Vulkan Vegas to jedno z najbardziej renomowanych kasyn online na rynku. Zyskało ono reputację nie tylko dzięki swojej bogatej ofercie gier, ale także szybkim wypłatom oraz uczciwym podejściem do graczy. Kasyno to oferuje szeroki wybór slotów, gier stołowych oraz kasyno na żywo. Co więcej, nowi gracze mogą liczyć na hojny bonus powitalny oraz regularne promocje.
2. EnergyCasino
EnergyCasino to kolejna znakomita opcja dla miłośników hazardu online. Znane z szybkich wypłat oraz doskonałej obsługi klienta, to kasyno przyciąga graczy nie tylko swoim bogatym wyborem gier, ale także atrakcyjnymi bonusami. Dodatkowo, EnergyCasino oferuje również możliwość obstawiania zakładów sportowych, co czyni je kompleksową platformą hazardową.
3. Betsson Casino
Betsson Casino to światowej klasy kasyno online, które od lat cieszy się uznaniem graczy na całym świecie. Oferuje ono nie tylko szeroki wybór gier, ale także doskonałą obsługę klienta oraz szybkie wypłaty. Dodatkowo, Betsson Casino regularnie organizuje turnieje oraz promocje, co dodaje dodatkowej wartości dla graczy.
Jak Oceniamy Najbardziej Wypłacane Kasyna Online?
Przy ocenie najbardziej wypłacanych kasyn online, KasynoPolska10 bierze pod uwagę kilka kluczowych czynników. Oto główne kryteria, które stosujemy:
Procent wypłat (RTP)
Procent wypłat, czyli Return to Player, jest kluczowym wskaźnikiem określającym, jak duża część zakładów dokonanych przez graczy zostaje zwrócona w formie wygranych. Im wyższy procent wypłat, tym korzystniejsza dla graczy sytuacja. Kasyna z wysokim RTP często uznawane są za najbardziej wypłacane.
Szybkość wypłat
Kolejnym istotnym czynnikiem jest szybkość wypłat. Kasyna online, które oferują szybkie wypłaty, zyskują zaufanie graczy i są uznawane za bardziej godne zaufania. Dlatego też przy ocenie kasyn bierzemy pod uwagę, jak szybko środki są wypłacane na konto gracza.
Oferta gier
Bogata oferta gier to również istotny element, który wpływa na ocenę kasyna online. Gracze szukają platform, które oferują szeroki wybór slotów, gier stołowych oraz kasyno na żywo, dzięki czemu mogą znaleźć rozrywkę dopasowaną do swoich preferencji.
Bonusy i promocje
Ostatnim, lecz nie mniej istotnym czynnikiem są bonusy i promocje oferowane przez kasyna online. Gracze szukają platform, które nie tylko oferują hojne bonusy powitalne, ale także regularne promocje oraz programy lojalnościowe, które nagradzają aktywnych graczy.
Podsumowanie
Wybór odpowiedniego kasyna online może być trudny, zwłaszcza w obliczu dużej liczby dostępnych opcji. Jednakże, biorąc pod uwagę kluczowe czynniki, takie jak procent wypłat, szybkość wypłat, oferta gier oraz bonusy i promocje, można znaleźć platformy, które są bardziej wypłacane i godne zaufania. W tym przeglądzie przedstawiliśmy trzy najbardziej wypłacane kasyna online według KasynoPolska10, które są znane z uczciwości, szybkich wypłat oraz doskonałej oferty gier. Mam nadzieję, że ta recenzja pomoże Ci podjąć najlepszą decyzję przy wyborze kasyna online.
Trading Anomalies
An extract from my new book, Equity Analytics.
Trading-Anomalies-2Applying Factor Models in Pairs Trading
A follow-up extract from my forthcoming book, Equity Analytics
Applying-Factor-Models-in-Pairs-Trading